图论
定义
图由定点(vertex)的集V和边(edge)的集E组成。
每一条边就是一幅点对(v,w)。
如果点对是有序的,则图是有向的,又称为有向图。
图中的一条路径是一个顶点序列:w1,w2,w3…wN是的(wi,wi+1)属于E。
如果有一个顶点v到它自身的的边(v,v),那么(v,v)也被称为环。
如果一个无向图中从每个顶点到其他每个顶点都存在一条路径,则称无向图是连通的,又称为强连通的。如果一个有向图不是强连通的,但是它的基础图图是联通的,那么有向图称为弱连通的。
完全图是其每一对顶点建都存在一条边的图。
图的表示
图是稀疏的,用邻接表(顶点表)表示;图是稠密的(|E|=O(V^2)),用邻接矩阵(二维数组)表示。
拓扑排序
拓扑排序是对有向无环图顶点的一种排序,使得如果存在一条从vi到vj的路径,那么在排序中vj就出现在vi的后面。拓扑排序不是唯一的。
拓扑排序首先要找到一个入度为0的点,将其加入到队列中,标记为已删除;将该顶点的邻接点入度减1;再继续寻找入度为0的点,直至所有顶点遍历完成。要注意判断是否有环。时间复杂度:O(|E|+|V|)。
public void topSort() throws CycleFoundException {
Queue q = new LinkedList();
int counter = 0;
for (Vertex v : directedGraph.values()) {
if (v.inDegree == 0) {
q.offer(v);
}
}
while (!q.isEmpty()) {
Vertex v = q.poll();
v.topNum = ++counter;
if (v.adjEdges != null) {
for (Edge edge : v.adjEdges) {
edge.endVertex.inDegree--;
if (edge.endVertex.inDegree == 0) {
q.offer(edge.endVertex);
}
}
}
}
if (counter != directedGraph.size()) {
throw new CycleFoundException();
}
} 最短路径
输入一个赋权图:与每条边(vi,vj)相联系的是穿越该路径的代价 ci,j 。 c(i,j) 可能是正,也可能是负。
赋权路径长是指一条路径 v1v2...vN 的值 ∑N−1i=1ci,i+1 。
无权路径长是指一条路径上的边数。
无权最短路径
只要经过的路径的边数最少就是无权最短路径。无权最短路径适用于无权无向图或者无权有向图(?)。
使用广度优先搜索:从开始顶点开始,按层次处理定点,先处理距开始点最近的顶点,最后处理最远的顶点。时间复杂度O( |v|2 )。
改进:使用队列保存 dv=currentDist 的节点。在处理 dv=currentDist 的过程中,将 dv=currentDist+1 的节点加入到队列。时间复杂度:O(|E|+|V|)。与拓扑排序类似。与拓扑排序不同的地方是:1 拓扑排序首先入队的是入度=0的点;最短路径算法首先入队的是源顶点。2 拓扑排序中当顶点入度=0可以继续入队;最短路径算法中是处理节点的邻边顶点且未处理过,就可以入队。
public void unweightedShortestPath(Vertex s) {
Queue q = new LinkedList();
for (Vertex v : directedGraph.values()) {
v.dist = Integer.MAX_VALUE;
}
s.dist = 0;
q.offer(s);
while (!q.isEmpty()) {
Vertex v = q.poll();
for (Edge edge : v.adjEdges) {
if (edge.endVertex.dist == Integer.MAX_VALUE) {
edge.endVertex.dist = v.dist + 1;
edge.endVertex.path = v;
System.out.println(edge.endVertex.vertexLabel+" 最短路径 "+edge.endVertex.dist+" 上一节点"+v.vertexLabel);
q.offer(edge.endVertex);
}
}
}
} 赋权最短路径–Dijkstra算法
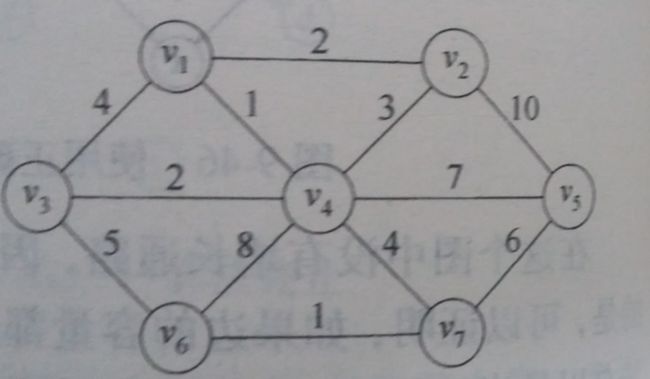
Dijkstra(迪克斯特拉,D-ijk-srtr-a)算法是贪心算法的一个例子,用来解决赋权有向图中,从单个顶点到其他顶点的最短路径。也可以用于赋权无向图。
算法描述:每个顶点维护两个属性:最短路径变量dist表源顶点到该顶点最短路径值;是否已知,如果处理过了就是已知。
在起始阶段设置所有顶点的【最短路径】=无穷大。源顶点s设置为 v3 。s.dist=0。
在每个阶段找到所有未处理顶点中dist最小值的顶点 vx 。 vx 的是否已知=已知,这相当于去掉了从上一步顶点到 vx 顶点的边。设置相邻顶点的dist。
证明:反证法证明这样做是有效的。
(这段描述有问题) v3 顶点是未处理顶点中具有最小dist的顶点。选择处理从v3到其他点权值最小的边处理。图中选择边(v3,v1)是最小权值的边。选择边(v3,v1),之后删除边(v3,v1),也就是v3和v1合为v1点,v1的最短路径=4。这被认为从v3到v1点的最小路径值。这里用反证法证明。假如(v3,v1)不是最短的,v3->vx->v1才是最短的,x!=1,也就是说 c3,x+cx,1<c3,1=4 ,那处理v3顶点的时候最小边就不是(v3,v1),而是(v3,vx),这与(v3,v1)是最小权值的边矛盾。这里局部最优就等于全局最优,因为这里的局部决策无后效性,当前决策不影响将来的决策。
Dijkstra算法选择一个顶点v,在所有未处理顶点中找到最小的 dv 。

以上图为具体例子。计算从 v1 到其他各个顶点的最短距离。初始表格如下:
| 顶点 | 是否已知 | 最短距离 | 上一步顶点 |
| v1 | F | 0 | |
| v2 | F | ∞ | |
| v3 | F | ∞ | |
| v4 | F | ∞ | |
| v5 | F | ∞ | |
| v6 | F | ∞ | |
| v7 | F | ∞ |
在[是否已知]=F,查找到【最短距离】最小的顶点 v1。 设置 v1 为已知。 v1 的邻接点 v2 , v4 计算得到最短路径值分别为:2,1。
| 顶点 | 是否已知 | 最短距离 | 上一步顶点 |
| v1 | T | 0 | |
| v2 | F | 2 | v1 |
| v3 | F | ∞ | |
| v4 | F | 1 | v1 |
| v5 | F | ∞ | |
| v6 | F | ∞ | |
| v7 | F | ∞ |
在[是否已知]=F,查找到【最短距离】最小的顶点 v4。 v_4 的邻接点 v_3 , v_5 , v_6 , v_7 。对 v_3 :分别设置3,v4。对 v_5 :3,v4。 v_5 , v_6$依序处理。
| 顶点 | 是否已知 | 最短距离 | 上一步顶点 |
| v1 | T | 0 | |
| v2 | F | 2 | v1 |
| v3 | F | 3 | v4 |
| v4 | T | 1 | v1 |
| v5 | F | 3 | v4 |
| v6 | F | 9 | v4 |
| v7 | F | 5 | v4 |
…
一直把所有节点处理完。得到从开始节点到每个其他节点的最小路径值。
注意:每个顶点处理一次,次数是|V|。在每次处理中,寻找【最短距离】顶点需要|V|。所以是 |V|2 。所有边会处理一次,所以是|E|。总运行时间为O(|E|+|V^2|)=O(|V^2|)。该方法只有在权值都为正数的情况下才有效。在下面这个有一条边为负,但没有负值圈的时候求得的结果是错误的。根据Dijkstra算法计算出从a到c最小路径值为2,而实际上是1。

如果图是稀疏的,时间复杂度可以使用优先队列或者堆进一步优化(这里没有完成)。
具有负权值的图的最短路径
一种方案是将所有权值加一个常数,使所有权值变为正数,行不通。例如从s到v有3条边,从s到u有5条边。如果每条边都增加4的话,s到v权重增加12,s到u权重增加15。这样不平衡。
一种解决方案是将上面无权重的和Dijkstra算法结合起来。让已经处理过的顶点反复进入队列,反复处理,直至队列为空。这将使得运行时间急剧增加。
关键路径分析法
关键路径分析法(critical path analysis),适用于无圈图。

关键路径分析法首先看动作节点图。图中的边代表优先关系:一条边(v,w)意味着动作v必须在w开始前完成。这意味着图必须是无圈的,否则依赖关系就会乱了。
关键路径分析法回答两个问题:方案最早完成时间是多少?确定哪些动作可以延迟,可以延迟多长,而不致影响最少完成时间?
1动作节点图转为事件节点图,在必要的地方引入哑边和哑节点。每个事件代表一个动作以及相关动作的完成。从节点v可以到达的事件,可以在事件v完成后开始。一个动作依赖于几个其他工作的情况下,可能需要插入哑边和哑节点。
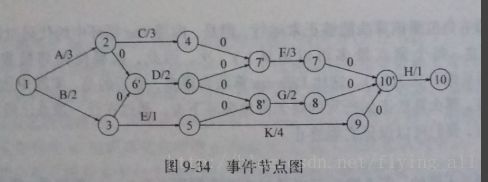
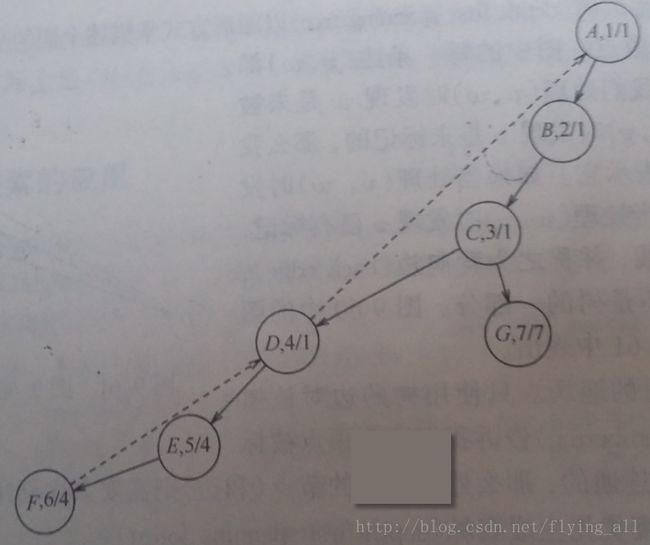
2找出最早完成时间。相当于找从第一个事件到最后一个事件的最长路径的长(关键节点一定在最长路径上,而且因为有依赖关系所以必须找最长路径。例如上图A->C->F->H需要10个时间单位。如果选择B->D->G->H需要7个时间单位,但是D开始必须在A和B都完成的情况下才可以。)。 ECi 是节点i最早完成时间。由于这是个无圈图,可以采纳最短路径算法计算图中所有节点的最早完成时间。
EC1=0
ECw=max(ECn+cc,w)
3 计算每个事件完成而又不影响最后完成时间的最晚时间 LCi 。从最后节点向前计算。
LCn=ECn
LCv=min(LCw−cv,w)
4 计算事件节点图中的松弛时间(slack time)。松弛时间代表对应动作可以被延迟而又不致于推迟整体完成的时间量。
Slack(v,w)=LCw−ECv−cv,w

5松弛时间为0的节点是关键性动作。至少存在一条完全由零松弛边组成的路径,这样的路径是关键路径。A->C->F->H
所有点对间最短距离
Floyed算法。类似动态规划,每次加入一个顶点。时间复杂度O(|V|^3)。
我们依序选择这些顶点。将定义 Dk,i,j 为从 vi 到 vj ,只使用 v1,v2,...,vk ,作为中间顶点的最短路径的权。根绝这个定义, D0,i,j=ci,j ,其中若 (vi,vj) 不是该图的边,则 ci,j=∞ 。当k>0时,从 vi 到 vj 使用或者不使用 vk 作为中间顶点。
Dk,i,j=min{Dk−1,i,j,Dk−1,i,k+Dk−1,k,j}
网络流量
有向图G=(V,E),其边容量为 cv,w 可以代表网络流量、水管的流量、人流量等。一个发点s,一个收点t。在从s到t的路径上,既不是发点,也不是收点的顶点v,总进入的流必须等于总发出的流。最大流量问题就是回答:从s到t最大流量是多少。
一种解决方法是使用流图 Gf 和残余图 Gr 。
1从 Gr 找到一条从s到t的路径。
2路径的每一步
在 Gf 生成对应的边(v,w);
Gr 在对应的边去掉 fv,w 的值,当值为零的时候去掉这条边;
在 Gr 画一条反向的边从w到v,变的值是 fv,w 。
重复直到2结束
3 重复1,直到知不道路径。
最小生成树
最小生成树是从一个图生成一棵树。有向图–>树,难度比较大。先处理无向图–>树。
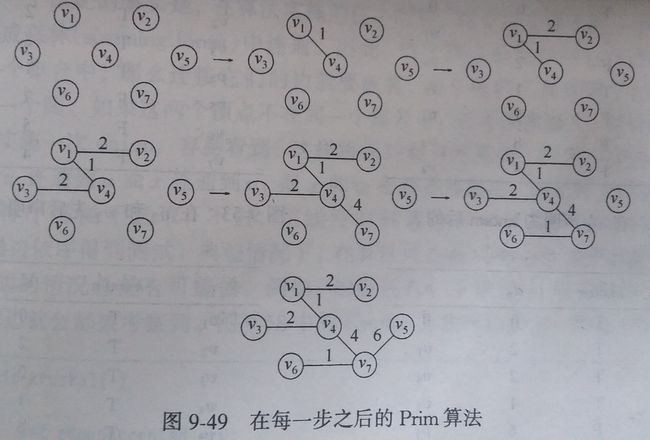
Prim算法
计算最小生成树的一种方式是使其连续地一步步成长。在每一步,都要把一个节点当做根,并往上加边。每一时刻,所有顶点分为已经添加到树上的,尚未加到树上的两部分。选择在树上的顶点u,选择边(u,v),v不在树上,而且(u,v)值是最小的,在所有尚未加到树上的顶点中。
Prim算法基本与Dijkstra算法相同。每次处理一个节点,每次寻找最小的边。
Kruskal算法
第二种解决方法是连续地选择最小权的边,并且当选择的边不产生圈的时候就使用这个边。开始的时候有|V|颗单节点树,而添加一条边将两棵树合并成一棵树。当算法终止的时候,只剩下一棵树了。关键步骤就是查找边(v,u)是不是应该添加。
深度优先搜索的应用
概念
深度优先搜索:从某个顶点v开始处理,然后递归的遍历所有与v邻接的顶点。与广度优选搜索不同,广度优先搜索是处理顶点v,处理与v距离为1的顶点,处理与v距离为2的顶点…..。如果图无向且不连通,或者有向但非强连通,这种方法可能会有些节点访问不到。解决方法是,多次调用深度优先搜索,每次的起点都是一个未访问过的顶点。深度优先搜索时间复杂度O(|E|)。
深度优先生成树
在无向图中,使用深度优先搜索生成树。如果图是非连通的,深度优先生成森林。如果处理边(v,w)w未被标记,那么就用一条边来表示,否则用一条背向边表示。
双连通性—找割点
一个连通的无向图,不存在被删除后使得剩下的图不再连通的顶点,那么这样的无向图是双连通的。
如果一个无向图不是双连通的,那么删除使得图不再连通的顶点叫割点。
查找割点的方法:
1 从图中任意顶点s开始,执行深度优先搜索,并在顶点被访问的时候给它们编号Num(v)。
2 为每个顶点计算编号最低的顶点Low(v)。计算方法有:a Low(v)=Num(v);b 所有背向边(v,w)中最低的Num(w);c 树的所有边(v,w)中最低的Low(w)。
3 根节点如果有两个或者两个以上的子节点,那根节点就是割点;非根节点v,如果v的某个儿子w使得Low(w)>=Num(v),那v就是割点。

欧拉回路
如果图G中恰好存在这样一条路径,使得它恰好经过图中的每一条边一次,同时该路径还是一个圈,则该路径称为欧拉回路。
如果图G存在欧拉回路,则图一定是连通的并且每个顶点的度是偶数。
如果图G是连通的并且每个顶点的度是偶数,则一定存在欧拉回路。两条件互为充要条件。
分享
分享一下我整理的图部分的知识图谱。第一张图是概要,第二张图内容完整。