算法导论第三版 22.3 深度优先搜索 课后题答案全解析
22.3 深度优先搜索:
1. 问有向图和无向图可能存在的三种颜色的点到点之间的边。
这个问题比较简单,直接上传原版答案,但是要注意,有向图中存在黑色点到其他点的边,虽然黑色点是已经搜索结束的,但是这样的边始终存在。
有向图:
无向图:
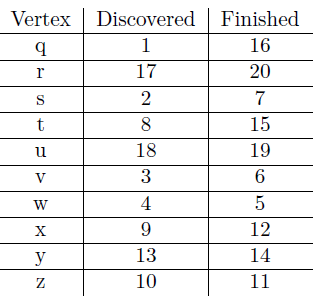
2. 答案如下:
注意其中数字没有重复的,无论如何time值都会+1。
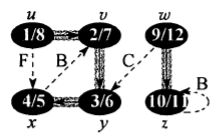
3. 给出括号结构,题目中要求的是22-4即下图:
因此括号结构应该为(((())))(()),作者认为参考答案解释有所不妥。
4. 与22.2中证明一位存储颜色类似。
5. 根据括号化定理可轻松证明,略。
6. 证明:在无向图中,根据深度优先搜索是先探索(u,v)还是先探索(v,u)来将边(u,v)分为树边或者后向边,与根据分类列表中的四种类型的次序进行分类是等价的。
证明:首先分类列表中的四种类型,树边、前向边、后向边、横向边,在无向图中只有树边和后向边。如果u、v之间的这条边,若从u→v方向进行搜索,若先发现的u,则是一条树边,然后v也被发现;若先发现的v,则u是v的祖先结点,因此这是一条后向边。和分类一致,得证!
7. 用Stack来实现深度优先搜索:
DFS(G){
for each vertex u belong G.V
u.color = WHITE
u.pai = NIL
time = 0;
for each vertex u belong G.V
if u.color ==WHITE
DFS_VISIT(G,u)
}
DFS_VISIT(G,u){
time = time + 1
u.color = GRAY
u.d = time
while stack != empty
v = stack.pop()
time = time +1
v.d = time
v.color = GRAY
for each vertex w adjacent to v
if w.color == WHITE
stack.push(w)
time = time +1
v.f = time
time = time +1
u.f = time
}用一个栈来代替循环,与网络大部分伪代码不同的是,该处加入了time来标记u.d和u.f。(该部分伪代码循环和条件的判断格式与算法导论书一致)
8. “有向图G包含一条从结点u到结点v的路径,并且在深度优先搜索中u.d
如图左中右三点,从中间点开始深度优先搜索,先找到左边的点,再找到右边的点,深度优先森林中右边的点不是左边点的后代,虽然在图中存在一条从左边的点到右边的点的路径。
9. “如果有向图G包含一条从结点u到结点v的路径,则任何对图G的深度优先搜索都将导致v.d<=u.f。”为这句话举出一个反例。
仍运用此图,如果深度优先搜索从中间点开始,先搜索右边点再搜索左边点,将会出现右边点的f小于左边点的d。
10. 修改深度优先搜索的伪代码,让其打印出有向图G的每条边及其分类。
深度优先森林有树边,后向边,前向边,横向边
(修改为粗体)
DFS(G)
for each vertex u belong to G.V
u.color = WHITE
u.pi = NIL
time = 0
for each vertex u belong to G.V
if u.color == WHITE
DFS-VISIT (G,u)
DFS-VISIT(G,u)
time = time + 1
u.d = time
u.color = GRAY
for each v belong to G:Adj[u]
if v.color == WHITE
输出(u,v)为树边
v.pi = u
DFS-VISIT(G,v)
if v.color == GRAY
输出(u,v)为后向边
if v.color == BLACK && v.f > u.d
输出(u,v)为前向边
if v.color == BLACK && v.f < u.d
输出(u,v)为横向边
u.color = BLACK
time = time + 1
u.f = time
如修改,在遍历到一个边的时候对v的color属性和f属性进行判断,将不同的边进行输出。如果是无向图,与有向图相比,无向图四种边没有什么区别,因此不需要进行调整。
11. 有向图的一个结点u怎样才能成为深度优先树中的唯一结点,即使结点u同时有入边和出边.
a) 首先结点u是一个自循环且只有自循环的结点。
b) 当一个点u出边指向的点已经被搜索结束属于其他深度优先树,并且接下来搜索点u,那么将会出现u是深度优先树中的唯一结点。
12. 证明略,内容在22.5强连通分支有详细讲解。
修改代码标记深度优先树,算导中DFS算法中,从图中找到一个新的结点的时候标记为x,然后在DFS-VISIT中将遍历到的每个white结点也标记为x。再回到DFS再找到一个新节点的时候标记为x+1,循环以上操作。
13. 判断图是不是单连通图。
首先进行拓扑排序。然后为每个结点维护一个链表,存储入度为0的祖先结点。
然后为每个点计算这些表根据拓扑排序从小到大的顺序。然后如果我们有一结点,它的两个以上的前驱结点的链表中包含同一个入度为0的祖先结点,我们可以知道,这不是单连通图了。相反,如果我们发现每个结点的前驱包含不相同的入度为0的结点,我们就可以判断这个图是一个单连通图。