深度学习源码剖析:使用双线性插值方式初始化神经网络的可训练参数
写在前面:
在深度学习领域中,双线性插值常常出现在研究者的视野中,在笔者主研的深度学习图像处理方面,也有很多地方使用到了双线性插值,比如下面的几个例子:
1. 在笔者之前的博文FCN训练不收敛的原因分析和最详细的FCN训练与测试自己的数据程序配置中,FCN训练不收敛的原因就是笔者没有使用双线性插值方式初始化反卷积层,导致模型训练不收敛。
2. 在著名的图像分割模型deeplab中,使用双线性插值的方式将最终的特征图放大以计算loss。
3. 在2017年Kaiming He的重磅之作Mask R-CNN中的ROIAlign这个创新点上,在将特征图上的目标逐像素与输入图像上的目标对齐的操作中,使用到了双线性插值。
由上所述,双线性插值在深度学习领域用途广泛,因此笔者打算在本篇博客中,借用一些源码,就双线性插值初始化神经网络可训练参数向读者朋友们做出剖析,不过在这之前,笔者想提醒各位读者朋友的是,如果大家对双线性插值的原理还不甚了解,请大家对双线性插值算法原理做出了解,该原理较为简单,笔者不再赘述,提供给大家一些了解双线性插值原理的相关入口:
1. 大饼博士X的博文三十分钟理解:线性插值,双线性插值Bilinear Interpolation算法,写的比较详细,在此对他表示感谢。该篇博文出自他的专栏http://blog.csdn.net/xbinworld
2. 维基百科:双线性插值
3. 百度百科:双线性插值原理
下面,笔者就来剖析一番双线性插值在初始化神经网络的可训练参数方面的应用。笔者打算利用两个例子来解析双线性插值初始化神经网络(反)卷积层的参数。第一个例子,是caffe官方提供的双线性插值参数初始化方式(c++)。第二个例子,是笔者在之前的博文中提到的,在FCN源码提供的的数据层中,使用的双线性插值参数初始化方法(python)。下面开始干货。1. caffe官方提供的双线性插值对卷积层参数的初始化。
有使用过深度学习框架caffe的读者朋友们应该知道,在我们训练模型的时候,会使用到定义网络架构的.prototxt文件,在该文件中,可以这样定义一个卷积层:
layer {
name: "conv"
type: "Convolution"
bottom: "bottom_blob"
top: "top_blob"
param {
lr_mult: 0
}
convolution_param {
num_output: 256
bias_term: false
kernel_size: 4
stride: 2
weight_filler {type: "bilinear"}
}
}如上代码所示,在卷积层中,我们使用了weight_filler进行了卷积层的权重参数的初始化操作,并且在其中传入了"bilinear"进行双线性插值初始化可训练权重参数的操作。然后我们紧接着来看一下caffe是怎么进行双线性插值初始化参数的。打开caffe根目录下面的include文件夹,再打开其中名为caffe的文件夹,在其中找到filler.hpp。我们在其中可以看到如下双线性插值初始化参数的代码,注释如下所示。
template
class Filler {//父类
public:
explicit Filler(const FillerParameter& param) : filler_param_(param) {}//空的构造函数
virtual ~Filler() {}//空的虚构函数
virtual void Fill(Blob* blob) = 0;//纯虚函数,需要在子类中重写
protected:
FillerParameter filler_param_;
}; // class Filler
//...
template
class BilinearFiller : public Filler {//子类
public:
explicit BilinearFiller(const FillerParameter& param)
: Filler(param) {}
virtual void Fill(Blob* blob) {
CHECK_EQ(blob->num_axes(), 4) << "Blob must be 4 dim.";//核验一下参数必须是四维的
CHECK_EQ(blob->width(), blob->height()) << "Filter must be square";//卷积核必须是正四边形
Dtype* data = blob->mutable_cpu_data();//在这里获取到需要被写入初始化值的可训练参数的起始地址
int f = ceil(blob->width() / 2.);//f是卷积核宽的一半,卷积核宽如果是奇数的话,则对商进行上取整操作
float c = (2 * f - 1 - f % 2) / (2. * f);//求得系数c,一个略小于1的值
for (int i = 0; i < blob->count(); ++i) {
float x = i % blob->width();//求得待写入值的行标
float y = (i / blob->width()) % blob->height();//求得待写入值的列标
data[i] = (1 - fabs(x / f - c)) * (1 - fabs(y / f - c));//写入被双线性插值初始化的权重参数,data[i] = (1-|(x/f)-c|)*(1-|((y/f)-c|)
}
CHECK_EQ(this->filler_param_.sparse(), -1)
<< "Sparsity not supported by this Filler.";
}
}; 看了如上的注释,我们用实例来分析一下这个BilinearFiller :: Fill(Blob
那么,在上面的代码中,先求得f为2,然后求得c为0.75(3/4),紧接着进入for循环:
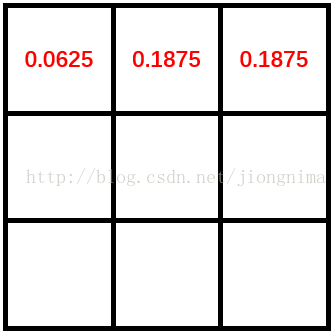
在i分别为0,1和2时,由于blob->width()为3,那么x分别为0,1和2,y恒为0。卷积核的第一行值被初始化,值为0.0625,0.1875和0.1875。见下图:在i分别为3,4和5时,x分别为0,1和2,y恒为1。卷积核的第二行值被初始化,值为0.1875,0.1875和0.5625。见下图:
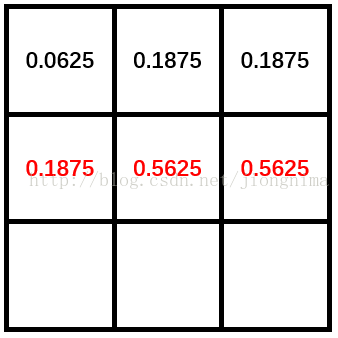
在i分别为6,7和8时,x分别为0,1和2,y恒为1。卷积核的第二行值被初始化,值为0.1875,0.1875和0.5625。见下图:
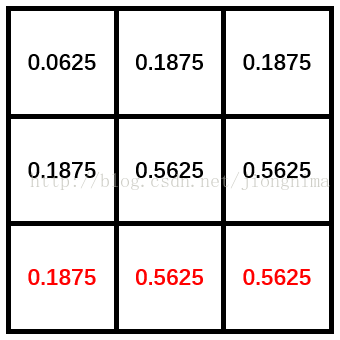
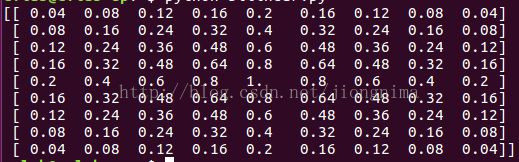
通过代码可以看出来,最终被初始化的参数在卷积核的长和宽方向是根据f对称的,在这里,也印证了代码中核验卷积核的长宽必须等同(卷积核必须是正四边形)是不可少的。那么,在上面的核的长宽都为3的情况下,为何看不到对称的情况呢?是因为f的值为2,对称中心点已经位于卷积核的右下角了,那么,我们换一个核尺寸大一些的情况分析一下,置卷积层的参数维度为[1, 1, 9, 9],那么,经过双线性插值初始化后的卷积核如下所示:
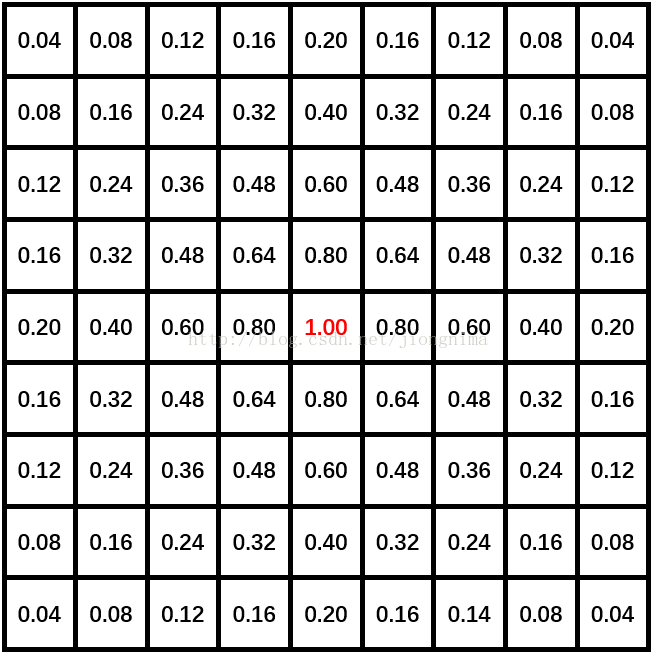
读者朋友们可以看到,初始化后的卷积核是关于坐标为(4, 4)的点对称的。对于不同尺寸的卷积核,读者朋友们可以自己分析双线性插值初始化参数后的结果。
2. fcn源码中的surgery.py文件中的对卷积核的双线性插值初始化。
surgery.py文件中的双线性插值初始化被用于初始化FCN中的反卷积层的参数。笔者在之前的博文中有提到。先放出代码及注释。
def interp(net, layers):
"""
Set weights of each layer in layers to bilinear kernels for interpolation.
"""
for l in layers:
m, k, h, w = net.params[l][0].data.shape
if m != k and k != 1:
print 'input + output channels need to be the same or |output| == 1'
raise
if h != w: #核验一下卷积核的宽是否等于卷积核的高
print 'filters need to be square'
raise
filt = upsample_filt(h) #求得双线性插值初始化的结果
net.params[l][0].data[range(m), range(k), :, :] = filt #赋值
def upsample_filt(size):
"""
Make a 2D bilinear kernel suitable for upsampling of the given (h, w) size.
"""
factor = (size + 1) // 2 #求得一个因子作为分母
if size % 2 == 1:
center = factor - 1 #如果核的尺寸是奇数,那么中心就是因子减1
else:
center = factor - 0.5 #如果核的尺寸是偶数,那么中心就是因子减0.5
og = np.ogrid[:size, :size] #ng返回一个列表,列表中有两个元素,第一个是一个size×1的二维数组,第二个是一个1×size的二维数组
return (1 - abs(og[0] - center) / factor) * \
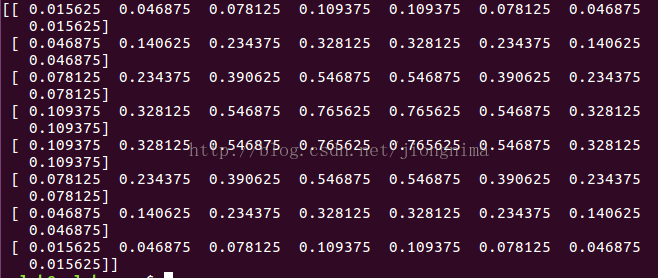
(1 - abs(og[1] - center) / factor) #在这里两个数据相乘(矩阵乘法),返回一个size×size的二维数组读者朋友们可以看到,在FCN源码处理双线性插值初始化反卷积层参数的时候,最终是通过一个矩阵相乘的形式实现的。并且,参数初始化后的卷积核也是关于center对称,值得注意的是,对于卷积核的尺寸分别为奇数和偶数时,upsample_filt函数的处理还不太一样,笔者还是列举两种情况给大家图示说明,首先是反卷积层参数规格为[1, 1, 9, 9]时候的双线性插值初始化后的卷积核,此时factor为5,center为4,双线性插值对卷积核的初始化结果如下图所示。
然后是反卷积层参数规格为[1, 1, 8, 8]时候的双线性插值初始化后的卷积核,此时factor为4,center为3.5,双线性插值对卷积核的初始化结果如下图所示。
笔者朋友们可以看到,由于卷积核尺寸为偶数,卷积核中没有任何值所在的位置是核的几何中心点。那么center则为3.5,不为整数,因此双线性插值初始化后的卷积核根据(3, 3),(3, 4),(4, 3),(4, 4)位置的点所构成的小正四边形对称。
到这里,双线性插值初始化神经网络层参数的样例源码说明就接近尾声了,衷心希望笔者的博文能对各位读者朋友们有启发,欢迎关注与分享!
欢迎阅读笔者后续博客,各位读者朋友的支持与鼓励是我最大的动力!
written by jiong
得道者多助,失道者寡助