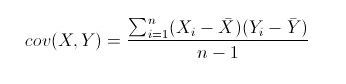python与协方差
方差是用来描述一维数据的偏差关系,而协方差是用来描述二维及以上的随机变量关系。协方差用cov方法表示,如cov(x,y)为正值,则x,y的关系是正相关的,为负则是负相关的,为0则没有关联。
看以下代码:
x=[-2.1, -1, 4.3]
y = [3, 1.1, 0.12]
X = np.stack((x, y), axis=0)此时X为:
array([[-2.1 , -1. , 4.3 ],
[ 3. , 1.1 , 0.12]])
此时,我们可以通过mean方法求x,y的平均值(期望), var方法求方差:
np.var(x) # 7.806666666666666
np.var(y) # 1.4294222222222224
np.mean(x) # 0.3999999999999999
np.mean(y) # 1.4066666666666665需要注意的是上面的var方法,默认是除以3,而下面的协方差则是除以3-1=2,可以通过ddof参数调节,即:
np.var(x,ddof=1) = np.cov(x)
通过cov求协方差:
np.cov(x,y)
#array([[11.71 , -4.286 ],
# [-4.286 , 2.14413333]])上面函数产生了四个值,排列起来如下:
cov(x,x)=11.71 cov(x,y)=-4.286
cov(y,x)=-4.286 cov(y,y)=2.14413333
这里面的值怎么来的?看下面公式:
按照上面的公式我们来算最后一个cov(y,y):
((3-np.mean(y))*(3-np.mean(y))+(1.1-np.mean(y))*(1.1-np.mean(y))+(0.12-np.mean(y))*(0.12-np.mean(y)))/2 算出来正好为2.14413333,其它值也是一样。
x与y相乘结果如下:
list(map(lambda a,b:a*b,x,y))
#[-6.300000000000001, -1.1, 0.516]