二叉搜索树(BST)的最近公共祖先(LCA)问题(Lowest Common Ancestor of a Binary Tree)
给定二叉搜索树中的任意两点,找出它们的最近公共祖先。
1、最近公共祖先(LCA)
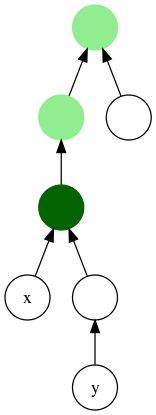
在上图这棵树中,绿色节点表示x和y的公共祖先,深绿色节点表示x和y的最近公共祖先(LCA)。
_______6______ / \ ___2___ ___8___ / \ / \ 1 _4_ 7 9 / \ 3 5以上图为例,1和4的最近公共祖先为2,1和7的公共祖先为6,还有另一种情况,当一个节点是另一个节点的时候,比如2和4的公共祖先为2还是6呢?根据维基百科的定义,这种情况下最近公共祖先为2。
2、算法思想
在第一幅图的树结构中,每一个节点指向父节点,因此从下往上直到根节点,找到x和y的第一个相交点,即为最近公共祖先。但在一般的二叉树结构中,每个节点只有指向子节点的指针,因此只能采用自上而下(top-down)的方法。根据二叉搜索树定义和的性质,按两个节点值和根节点值的关系,可分为以下四种情况:
a、两个节点都在树的左子树上;
b、两个节点都在树的右子树上;
c、一个节点在左子树,一个节点在右子树;
d、当前节点的值和其中一个节点的值相等。
以第二幅图为例,节点1和节点4为情况a,节点7和节点9为情况b,节点1和节点7为情况c,节点2和4为情况d。
若为情况c或d,当前节点即为最近公共祖先,若为情况a或b,则还需递归到左或右子树上,继续这个过程。
该算法的时间复杂度为O(h),h为树的高度。
3、代码和数据结构
二叉搜索树数据结构可定义为:
// Definition for Binary tree. struct TreeNode { int val; TreeNode *left; TreeNode *right; // constructor TreeNode(int x) : val(x), left(NULL), right(NULL) {} };
有了以上的分析,可以很快写出递归代码:
// recursive LCA TreeNode *LCA(TreeNode *root, TreeNode *p, TreeNode *q) { if (!root || !p || !q) return NULL; if (max(p->val, q->val) < root->val) // 情况a return LCA(root->left, p, q); else if (min(p->val, q->val) > root->val) // 情况b return LCA(root->right, p, q); else // 情况c,d return root; }
由于是以上代码为尾递归算法,很容易写出其迭代版本。
// iterative LCA TreeNode *LCA(TreeNode *root, TreeNode *p, TreeNode *q) { if (!root || !p || !q) return NULL; while(true) { if (max(p->val, q->val) < root->val) root = root->left; else if (min(p->val, q->val) > root->val) root = root->right; else return root; } }
上边都只考虑了给定的节点一定是在二叉搜索树种存在的,若该节点在二叉搜索树中不存在,在还需加上一个判断该节点是否在树中的子函数。
// 判断节点p是否在树中 bool contains(TreeNode *root, TreeNode *p) { if( root == NULL) return false; if( p->val < root->val ) return contains(root->left, p); else if( p->val > root->val ) return contains(root->right, p); else return true; }
最后,加上判断后的完整二叉搜索树最近公共祖先问题的求解代码如下: TreeNode *LCA_BST(TreeNode *root, TreeNode *p, TreeNode *q) { if( contains(root, p) && contains(root, q) ) { return LCA(root, p, q); } return NULL; }