谈谈经典限流方法——漏桶、令牌桶，与Guava RateLimiter的实现

前言

昨晚对球迷来说简直是盛宴（边霍啤酒边看了4场球），当然也导致本篇没写完。

那么今天就来续一发吧。

高并发的业务系统经常要接受大流量的考验，为了保证系统的响应度和稳定性，往往都需要对有风险的接口实施限流（rate limiting），更高大上的说法则是“流量整形”（traffic shaping）。限流的思想最初来源于计算机网络，有两种经典的方法：漏桶和令牌桶。本文先来稍微研究一下它们。

漏桶（Leaky Bucket）

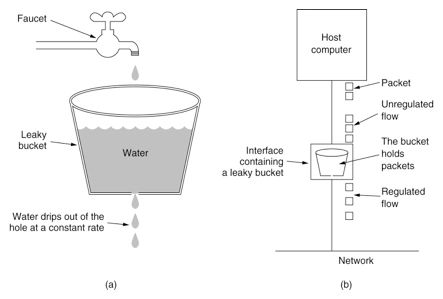
将请求想象成水龙头里流出的水，接口中有一个底部开孔的桶，如下图所示。

这样就能使请求处理的速率有一个稳定的上限。很显然，如果进水的速率比开孔出水的速率大的话，水（请求）就会逐渐在桶中积累。若一直积累直到溢出了，那些溢出去的水（请求）就会被直接丢弃，也就是拒绝服务（denial of service, DoS）。

漏桶的思路非常简单直接，易于实现。但是如果当前的网络环境中充斥着短时流量尖峰，始终保持匀速的漏桶就无法很好地处理了，故后来又产生了令牌桶算法。

令牌桶（Token Bucket）

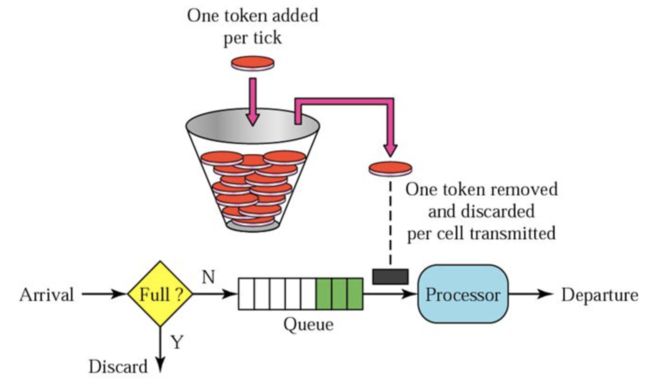
顾名思义，令牌桶里放的不再是请求，而是令牌，可以理解为处理请求的通行证。如下图所示。

令牌以恒定的速率产生并放入桶中。桶的大小是有限的，也就是说桶满了之后，多余的令牌就扔掉了。每当请求到来时，需要从桶中获取一个令牌才能真正地处理它。如果桶里没有令牌，该请求就会被丢弃。

可见，由于桶里预先留有一定量的令牌，故可以保证在突发流量到来且令牌没耗尽前平滑地处理，比漏桶更灵活一些。

在很久之前的文章《深入理解Spark Streaming流量控制及反压机制》中，曾经说过Spark Streaming的限流是靠令牌桶来实现的，具体来讲是Google Guava提供的限流器——RateLimiter。它的设计比较聪明，下面简单地看一看。

Guava RateLimiter

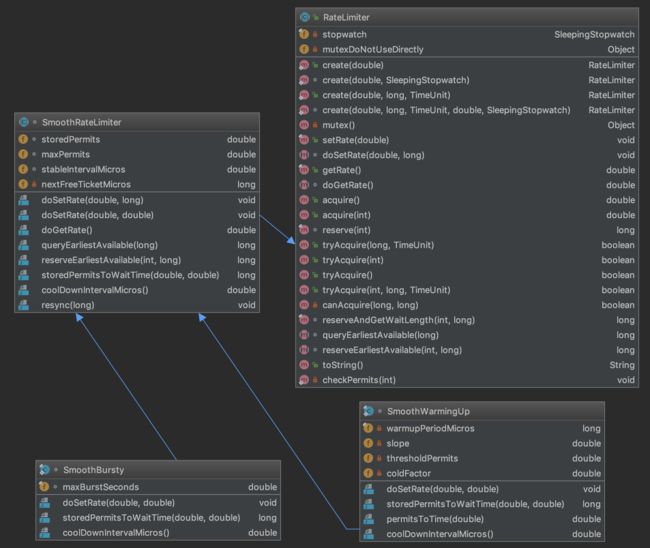
类图如下，字有点多哈。

RateLimiter抽象类提供限流的所有功能，它的实现类只有SmoothRateLimiter。而SmoothRateLimiter的具体策略又由它的两个内部子类来实现。

• SmoothBursty：兼容突发流量的令牌桶实现，也就是上一节描述的经典令牌桶算法。
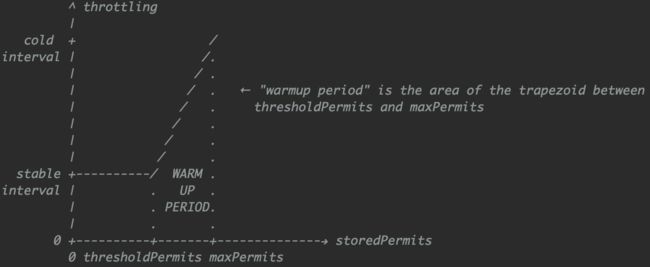
• SmoothWarmingUp：带预热过程的令牌桶实现，即在桶较满时产生令牌的速度较慢，随着令牌的消耗慢慢增长到恒定速率。如下图所示，x轴为令牌数，y轴为延迟，从右向左看的梯形区域就是令牌消耗的预热过程。

本文以经典的SmoothBursty为范本来讲。先说明一下SmoothRateLimiter的4个属性的含义，它们都非常重要。

• storedPermits：当前桶里有的令牌数量。
• maxPermits：桶装满时的令牌数量，storedPermits不会比它大。
• stableIntervalMicros：产生令牌的频率（时间间隔），单位为微秒。举个栗子，如果我们想限制系统的QPS为10，亦即每秒有10个令牌放入桶中，那么stableIntervalMicros的值就是100000。
• nextFreeTicketMicros：下一个令牌可用的时间戳，也就是下一个请求能够被处理的时间戳，单位为微秒。该值会随着当前请求获得令牌而增大（因为时间是自然流动的）。若当前请求的令牌数超出可用令牌数，这个时间就被推后（需要时间产生新的令牌）。当然，如果有一段时间没有请求进入的话，它就会保持在上次请求的过去时间戳。

RateLimiter要发挥作用，首先得产生令牌，由SmoothRateLimiter.resync()方法来实现。

  void resync(long nowMicros) {
    if (nowMicros > nextFreeTicketMicros) {
      double newPermits = (nowMicros - nextFreeTicketMicros) / coolDownIntervalMicros();
      storedPermits = min(maxPermits, storedPermits + newPermits);
      nextFreeTicketMicros = nowMicros;
    }
  }

  // SmoothBursty.coolDownIntervalMicros()
  @Override
  double coolDownIntervalMicros() {
    return stableIntervalMicros;
  }

在当前时间戳大于nextFreeTicketMicros（即后者是一个过去的时间戳）的情况下，就用它们的时间差除以产生令牌的频率，结果就是这段时间内应该产生的令牌数，进而更新桶内的现有令牌数storedPermits，以及将nextFreeTicketMicros更新到现在。

可见，RateLimiter的令牌是延迟（lazy）生成的，也就是说每次受理当前请求时，如果系统已经空闲了一定时间，才会计算上次请求到当前时间应该产生多少个令牌，而不是使用单独的任务来定期产生令牌——因为定时器无法保证较高的精度，并且性能不佳。当然，如果令牌已经“超支”，当前就不需要再更新令牌了。

接下来则是获取令牌，由SmoothRateLimiter.reserveEarliestAvailable()方法来实现，这个方法名非常self-explanatory了。

  @Override
  final long reserveEarliestAvailable(int requiredPermits, long nowMicros) {
    resync(nowMicros);
    long returnValue = nextFreeTicketMicros;
    double storedPermitsToSpend = min(requiredPermits, this.storedPermits);
    double freshPermits = requiredPermits - storedPermitsToSpend;
    long waitMicros =
        storedPermitsToWaitTime(this.storedPermits, storedPermitsToSpend)
            + (long) (freshPermits * stableIntervalMicros);

    this.nextFreeTicketMicros = LongMath.saturatedAdd(nextFreeTicketMicros, waitMicros);
    this.storedPermits -= storedPermitsToSpend;
    return returnValue;
  }

  // SmoothBursty.storedPermitsToWaitTime()
  @Override
  long storedPermitsToWaitTime(double storedPermits, double permitsToTake) {
    return 0L;
  }

这个方法的执行流程如下：

1. 调用上述resync()方法产生令牌。
2. 计算实际能提供的令牌数storedPermitsToSpend，它其实就是本次请求需要的令牌数requiredPermits和桶中有的令牌数storedPermits的较小值。
3. 计算需要新产生的令牌数freshPermits。当上一步桶中有的令牌不够用时，该值就大于0。
4. 根据freshPermits计算新产生这批令牌需要多长时间，记为waitMicros。由于SmoothBursty始终以恒定速率产生令牌，只需要将它与令牌产生的速率简单相乘就行。SmoothWarmingUp需要考虑预热的延时，所以storedPermitsToWaitTime()方法实现要复杂得多。
5. 更新nextFreeTicketMicros和storedPermits的值。

弄明白了产生令牌和获取令牌的细节，我们回到RateLimiter的顶层，看看它到底是如何发挥作用的。

Guava提供了多个静态create()方法创建RateLimiter，其中创建SmoothBursty的源码如下。

  public static RateLimiter create(double permitsPerSecond) {
    return create(permitsPerSecond, SleepingStopwatch.createFromSystemTimer());
  }

  @VisibleForTesting
  static RateLimiter create(double permitsPerSecond, SleepingStopwatch stopwatch) {
    RateLimiter rateLimiter = new SmoothBursty(stopwatch, 1.0 /* maxBurstSeconds */);
    rateLimiter.setRate(permitsPerSecond);
    return rateLimiter;
  }

可见，我们创建RateLimiter时只需要指定期望的QPS。那么SmoothBursty构造方法中的maxBurstSeconds参数有什么用？顾名思义，它表示在令牌桶满时能够承受的突发流量时长，这样就能够确定出桶的最大容量maxPermits了：

maxPermits = maxBurstSeconds * permitsPerSecond;

不过maxBurstSeconds当前不支持自定义，Guava规定为1秒，故桶的最大容量总是与我们指定的QPS相同。

RateLimiter向用户提供了acquire()方法用于获取令牌，以及带超时的tryAcquire()方法。下面的代码示出从acquire()到reserveEarliestAvailable()的调用链，方法都很短。

  @CanIgnoreReturnValue
  public double acquire() {
    return acquire(1);
  }

  @CanIgnoreReturnValue
  public double acquire(int permits) {
    long microsToWait = reserve(permits);
    stopwatch.sleepMicrosUninterruptibly(microsToWait);
    return 1.0 * microsToWait / SECONDS.toMicros(1L);
  }

  final long reserve(int permits) {
    checkPermits(permits);
    synchronized (mutex()) {
      return reserveAndGetWaitLength(permits, stopwatch.readMicros());
    }

  final long reserveAndGetWaitLength(int permits, long nowMicros) {
    long momentAvailable = reserveEarliestAvailable(permits, nowMicros);
    return max(momentAvailable - nowMicros, 0);
  }

可见：

• 获取令牌的过程是加锁的。
• reserveAndGetWaitLength()返回的是获取令牌需要等待的时间，在acquire()方法中会借助Stopwatch阻塞（睡眠）直到获取成功。Stopwatch是Guava自行实现的一个高精度计时器。
• acquire()方法会将上述等待时间返回，但不需要用户再处理了，所以该返回值可以忽略（即@CanIgnoreReturnValue注解的含义）。

最后举个简单的例子吧。

public class RateLimiterExample {
  public static void main(String[] args) throws Exception {
    RateLimiter rateLimiter = RateLimiter.create(10);
    Random random = new Random();
    for (int i = 0; i < 20; i++) {
      int numPermits = random.nextInt(20);
      System.out.println(numPermits + "\t" + rateLimiter.acquire(numPermits));
    }
  }
}

运行结果如下。

2   0.0
13  0.198792
4   1.294088
6   0.39622
18  0.59516
12  1.797798
14  1.198664
14  1.397321
13  1.39626
16  1.299534
3   1.595453
9   0.299325
4   0.898857
18  0.394973
2   1.795835
13  0.195926
11  1.294851
2   1.09551
3   0.194857
6   0.297884

可见，每次获取的令牌数和获取时需要等待的时长是符合上面所述逻辑的预期的。

The End

今天大风降温，该把羽绒服毛衣之类的家伙搬出来了。

民那晚安。