回溯算法

回溯算法

回溯算法是用于树上的一种暴力搜索算法，它通常使用深度优先遍历来搜索问题的所有可行解。它在搜索的过程中，如果发现不满足问题的约束条件，则回溯到上一层的父节点a，从与a节点相同深度的邻节点b继续进行搜索；如果我们遍历到了最底层的节点，说明该路径上的所有节点可以组成该问题的一个可行解。然后我们返回到上一层，继续遍历其他节点，直至遍历完树上所有的节点。这就是回溯算法的基本思想。

我们以走迷宫游戏为例，我们把所有的分岔路口当作一个节点，入口相当于树的根节点，出口是树的底层节点。从入口的第一个路口开始，随机选择一条路径往前走，到了下一个路口再随机选择一条路径。当我们发现路径走不通时，我们就返回到上一个路口，选择另一条路径；倘若该路口的所有路径都走不通，我们就回到上上一个路口，选择另一条路径…直到走出迷宫，则我们之前选择的所有路径可组成一条走出迷宫的路线。然后我们再返回到上一个路口搜索其他的走出迷宫的路线。

回溯算法通过遍历能找出多个问题的可行解，我们可以根据实际情况选择最优的解。典型的例子还有八皇后问题，数组元素全排列问题以及着色问题等等。

使用回溯算法时，经常会使用到深度优先遍历、递归以及剪枝。

深度优先算法(DFS)

使用深度优先算法能够直接使用系统栈保存节点信息，而广度优先遍历则需要我们自己去编写节点类和使用队列。因此，在回溯算法中采用DFS能使得编码更加简单。

剪枝

在求解问题时，我们偶尔能提前知道某些路径是不通的或者没有意义的，这时候就可以采用“剪枝”的方式来减小算法的复杂度。尤其是当搜索算法的状态空间庞大时，剪枝是一种能有效提高效率的方法。

求解八皇后问题（java代码）

问题描述

八皇后问题指的是在8*8的棋盘内放置8个皇后棋子，且要求任意两个棋子不能在同一行、同一列、同一对角线上。要求我们找出符合问题要求的棋子的所有摆法。

求解思想

我们容易知道，每一行都只会有一个棋子。假设八个棋子的位置分别设为坐标 (x(n), n)，即n行x(n)列（n=1,2,…,8）。题目的要求即可以转换为任意两个坐标点 (x(i), i)， (x(j), j) （i != j）要满足以下条件：

纵坐标不同：x(i) != x(j)
斜率不等于正负1：(i-j) != x(i)-x(j)

代码实现

public class trackBack_queen {//N皇后
	int num=0;
	int N=8;
	int x[]=new int [N];
	
	public void trackBack(int n) {
		if(n==N) {
			for(int i=0;i<N;i++) {
				System.out.print(x[i]+" ");
			}
			System.out.println();
			num++;
			return;
		}
		for(int i=0;i<N;i++) {
			x[n]=i;//n行i列
			boolean p=true;
			for(int j=0;j<n;j++) 
				if(x[j]==x[n]||Math.abs(j-n)==Math.abs(x[j]-x[n]))
					p=false;
			if(p)
				trackBack(n+1);
		}
	}
	
	public static void main(String[] args) {
		trackBack_queen e = new trackBack_queen();
		e.trackBack(0);
		System.out.println("解法种数： " + e.num);
	    }
}

输出结果：共92种摆法（各种摆法的棋子位置可运行代码查看）。

求解数组元素全排列问题（java代码）

问题描述

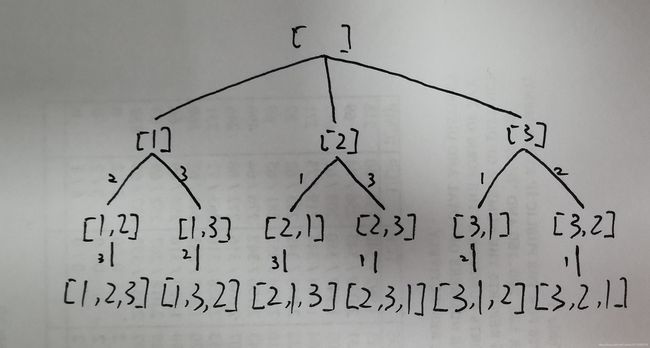
给定一个数组｛1，2，3｝，让我们用里面的元素进行全排列。
如数组｛1，2｝有两种排列方式：｛1，2｝和｛2，1｝。

求解思想

这是最简单也是最典型的回溯算法的应用，直接通过回溯算法的思想即可找到所有解。

代码实现

public class trackBack {
	int num=0;
	
	public static void main(String []args) {
		trackBack e=new trackBack();
		int arr[]= {1,2,3};
		int k=0;
		e.trackBack(arr, k);
		System.out.print("排序数量："+e.num);
	}

	public void trackBack(int arr[], int k) {
		if(k==arr.length-1) {
			for(int j=0;j<arr.length;j++) {
				System.out.print(arr[j]+" ");
			}
			System.out.println();
			num++;
		}
		for(int i=k;i<arr.length;i++) {
			int K=arr[i];
			arr[i]=arr[k];
			arr[k]=K;
			trackBack(arr, k+1);
			K=arr[i];
			arr[i]=arr[k];
			arr[k]=K;
		}		
	}
}

输出6种排列方式：

1 2 3 、1 3 2 、2 1 3 、2 3 1 、3 2 1 、3 1 2

用剪枝来求解含有相同元素的全排列问题

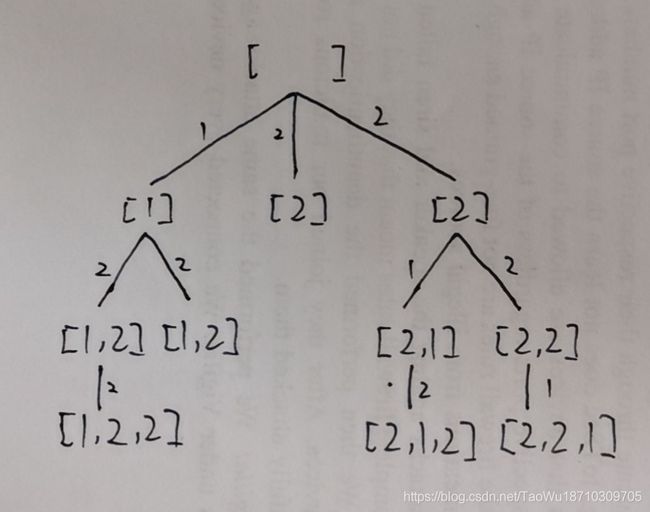
上面的例子｛1，2，3｝中不含有重复元素，比较简单。如果我们要求解｛1，2，2｝的全排列问题，使用上面的方法会输出重复的排列方式：

1 2 2 、1 2 2 、2 1 2 、2 2 1 、2 2 1 、2 1 2

但我们可以通过剪枝的方法来将其中的重复部分删除掉：在同一深度中存在相同的节点，则保留一个节点，且把其它相同节点及其子节点全部剪掉。

代码实现如下

public class trackBack_Cut {//	全排列：回溯+剪枝
    int num=0;
	
	public static void main(String []args) {
		trackBack_Cut e=new trackBack_Cut();
		int arr[]= {1,2,2};
		int k=0;
		e.trackBack_Cut(arr, k);
		System.out.print("排序数量："+e.num);
	}

	public void trackBack_Cut(int arr[], int k) {
		if(k==arr.length-1) {
			for(int j=0;j<arr.length;j++) 
				System.out.print(arr[j]+" ");
			System.out.println();
			num++;
		}
		for(int i=k;i<arr.length;i++) {
		    boolean p=true;
			for(int j=i+1;j<arr.length;j++) {//剪枝：如果同一深度，i元素后面有与i相同的值，则剪枝，跳过该次递归
		    	if(arr[j]==arr[i]) {
		    		p=false;
		    		break;
		    	}
		    }
			if(p) {
				int K=arr[i];
				arr[i]=arr[k];
				arr[k]=K;
				trackBack_Cut(arr, k+1);
				K=arr[i];
				arr[i]=arr[k];
				arr[k]=K;
			}
		}		
	}
}

输出3种排列方式：

1 2 2 、2 2 1 、2 1 2

今天的分享就到这里啦，欢迎大家一起交流指正！