最长上升子序列练习总结
#最长上升子序列
经典模板题poj3903
灵活变形题poj1631
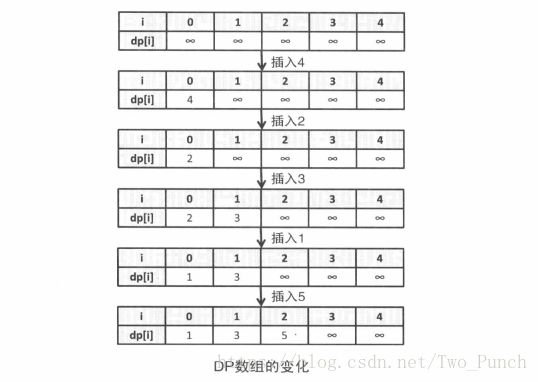
虽然说最长上升子序列问题用n^2的复杂度也可以解决,但是这道题确实是不得行的,所以又学到了新方法,用二分法,所以用的dp思路也不一样了,至于具体啥子情况,就看下图了
![]()
##lower_bound()方法
所以每次只用确定最第一个大于置顶元素的位置,就是用二分法来确定,但是algorithm里面已经有现成的了,就是lower_bound()方法
参考博客 lower_bound()方法
然后就是代码了
#include第二题poj1836
这道题说是菜那是凶,我开始还以为就只是套路就行了,哪晓得还有点东西。
这道题说一个团的人站成一排(因为n限制最大是1000,肯定不止一个排,就算加强排也不可能这么多人,就当一个团嘛,虽然人少点,就当才从坂田联队正面突围的团),但是没有按身高排好,所以,独立团团长就很不爽了!(兵熊熊一个将熊熊一窝,他娘的,排个队都排不好,旅长又得骂咱是发面团了),然后团长就会叫一些人出列,然后剩下的人组成一个新的队列,这个新队列特点就是其中任意一位弟兄,不管他是往左边看还是往右边看都可以看到头,就是左或者右没得都是比他矮的,长得一样高都不得行。
我的第一反应就是,哎呀,不就是最长上升子序列和最长下降子序列都找出来,然后比较哪个的长度大,然后用总的人数减去那个最长长度就是答案了
就好比这样

和

但是紧到WA,我就研究啊,最后反应过来一个东西,确实最长上升子序列和最长下降子序列都可以满足任一朝左或者朝右都一颗看到头,但是还有种情况

对啊,反正只要中间高咋个看都看得到两边的东西~而且中间的人还可以相等。
但是,这个又咋个是实现喃?最长上升子序列又不是最长下降子序列,是两个合体

实现就是在一个一个找最长上升子序列的同时,也就是没找到一个最长上升子序列中的元素就开始往后找最长下降子序列,也就是。。。上图
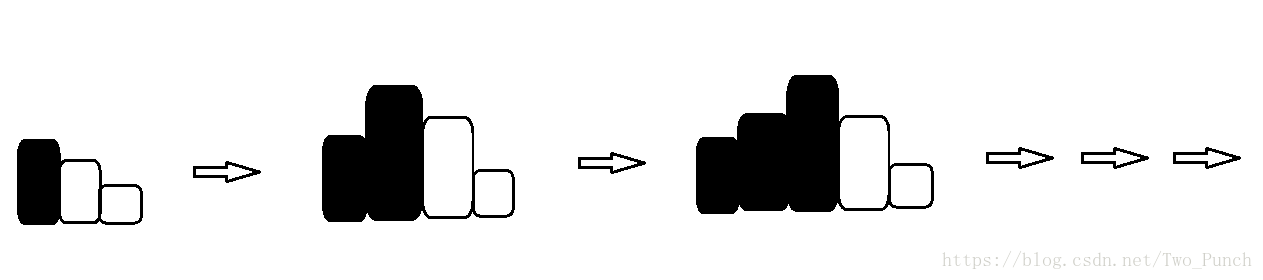
之前用lower_bound()方法只能求第一个大于或等于的位置,但是要求最长下降子序列的时候就要找第一个小于或等于的位置,这个时候感觉lower_bound()好像没得办法完成这个功能,但是,神奇的lower_bound()方法还有一个重载的方法就是增加一个参数
lower_bound(arr, arr + length, value, greater
这个greater 还是比较方便,但是用的时候要引入#include
其实这样复杂度都O(n^2logn)了, 幸好这个团人才1000,但是如果遇到当年我打平安县城那会儿,我手底下可是有八个营的部队,连张大彪一个营就有2000多人,加上各种县大队、区小队, 还包括战斗打响后来帮忙的老孔和老丁,还有云飞兄都来帮忙了~ 可以说这上万人的部队多半要超时。。。
#include第三题poj1065
这道题又把我整腾儿了。。。这道题是说有一堆木棍儿,有长度和重量两个属性,然后就是求最少有几个上升子序列,我开始的时候有了一个自认为很炫的想法,但是,自认为很妙的想法就把我方向带偏了,还没抵拢就倒拐了。。。然后就回不来了
我开始想的这的序列有两个属性,直接排麻烦,先取其中一个属性比如就先取长度,以长度来升序排序,如果长度相等就以重量来排,然后其实就把两个属性的序列,转化成只有一个参数的序列,就用lower_bound()来最长上升子序列的套路。然后定义一个tag数组,初始化为0,只要再找最长上升子序列的过程中定位到某个位置,就在这个位置自加1。 把最长上升子序列过程走完过后,就切tag数组中找最大的那个就是答案了。之所以要自加即使因为我感觉既然这个位置有重复的那么就有不同的序列,就该加1。 而且!!!这个复杂度可是O(nlogn)啊~,还是相当快的,自认为还可以,但确实是错的,错代码就不粘上来了。
反正还是想了多久感觉就是对的但就是WA,也不晓得为啥子错了,然后我切网上找有没得测试数据,确实还找到一个。
直接就来把问题转化为只有重量(长度也一样,反正就把两个属性的最长上升子序列转化成只有一个属性的最长上升子序列)
比如转化成:3 ,7 , 5 , 2
然后如果以最长上升子序列那个套路就是不停覆盖,就是这种覆盖出的问题。。
第一层 : 3 , 7
第二层 : 2 , 5
而这个时候tag数组自加就是:2 , 2 , 结果就成了2个序列
但是应该是 :
一 、 3 , 7
二 、 5
三 、 2
这三个子序列。
根据这个例子我突然豁然开朗,山重水复疑无路~ 柳暗花明又一开~ , 然后又瓜兮兮的想了一个自认为绝妙的方法,但是又错了。。。我想的是用lower_bound() 每次确定一个位置 i 的时候,先把tag [ i ] 这个值++ , 然后把前面每一个小于 tag [ i ] 的值都变成 tag [ i ]. 然后就对了三~,还是WA 。 然后我又找反例,要不然晓得到底错到哪在。
比如 : 2 , 7 , 4 , 6 , 5
第一层覆盖 : 2 , 7
第二层覆盖 : 2 , 4 , 6
第三层覆盖: 2 , 4 , 5
tag的值就是:1 , 2 , 2, 所以组后找出来是2,但是应该是
一 、 2 , 7
二 、 4 , 6
三 、 5
应该是3个序列
所以问题就出在覆盖。覆盖会让本来不该在一个子序列的元素变到同一个序列中,因为覆盖就是把比当前值小的元素覆盖上去,就比如 B 覆盖了 A , 那么就是因为 B < A ,这就会导致后面某一个元素本来不能被 A 覆盖的但是因为 B 把 A 覆盖了, 就相当于后面的数据都在判断是某跟B在一个序列中, 而B只用判断一次,但是tag数组对应位置的值还是从0加起走,也就是默认可以跟 A 在一个序列中, 也就是相当于本来不能被A 覆盖的元素,因为A 被 B 覆盖了 。。。 你懂~
然后我放弃了这种 O(nlogn) 的方法, 我回到了正轨~ 就是 O(n^ 2)的方法,也就是两重循环, 就是让第一层循环就是不停找每个序列的第一个,然后第二重循环就是在第一层基础上切找所有大于前面的元素,然后把找了的元素置为inf,免得下一次找重了,而且他数据最大也才5000,就是让O(n^ 2)神得起
还是 : 2 , 7 , 4 , 6 , 5
一 : inf , inf , 4 , 6 , 5
二 : inf , inf , inf , inf , 5
三 : inf , inf , inf , inf , inf
之所以这样就是对的,因为每一层循环其实都是把能找到的最小的先收了,然后剩下大的,把大的值留给后面层的循环会使得每次都是找的每个元素最长子序列,因为每个元素始终都要找一个归属序列
#include