2015-12-17晚,复习,甚是无聊,阅《复杂网络算法与应用》一书,得知最小生成树问题(Minimum spanning tree)问题。记之。
何为树:连通且不含圈的图称为树。
图T=(V,E),|V|=n,|E|=m,下列关于树的说法等价:
- T是一个树。
- T无圈,且m=n-1。
- T连通,且m=n-1。
- T无圈,但每加一新边记得到唯一一个圈。
- T连通,但任舍去一边就不连通。
- T中任意两点,有唯一道路相连。
何为生成树:若图G=(V,E)的生成子图是一棵树,则称该树为图G的生成树,也称支撑树,简称为图G的数。图G中属于生成树的边称为数枝(Branch)。
何为最小生成树:连通图G=(V,E),每条边上有非负权L(e)。一棵树上所有树枝权的总和,称为这个生成树的权。具有最小权的生成树称为最小生成树,也就是说最小支撑树,简称最小树。
私以为,两种算法其实都是贪心,所以需要严格的证明。由于最近时间零散、数学久置未学、对算法领域没有系统了解。所以不进行深入探讨(也就是说证明),仅以一个简单实例做一个入门级的了解。
Prim算法:
给定连通赋权图G=(V,E,W),其中W为邻接矩阵,设两个集合P和Q,其中P用于存放G的最小生成树中的节点,集合Q存放G的最小G的最小生成树中的边。另集合P的初值为P={v1}(假设构造最小生成树时从v1出发),集合Q的初值为P={空集}。
(1)P = {v1},Q = {空集};
(2)while P ~= Q
找到最小边pv,其中p∈P,v∈V-P;
P = P + {v};
Q = Q + {pv};
end
Kruskal算法
(1)选e1∈E(G),使得w(e1) = min(选e1的权值最小)。
(2)e1,e2,...,ei已选好,则从E(G)-{e1,e2,...,ei}中选取ei+1,使得G[{e1,e2,...,ei,ei+1}]中无圈,且,w(ei+1) = min。
(3)直到选得en-1为止。
以下是问题:
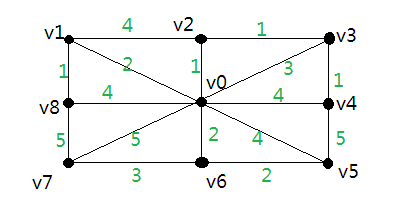
一个乡有9个自然村,其间道路及各道路长度如图所示,各边上数字代表距离。问如何架设电线最短。
预输入:
1 A = zeros(9); 2 A(1,2:9) = [2 1 3 4 4 2 5 4]; 3 A(2,[3, 9]) = [4 1]; 4 A(3, 4) = 1; 5 A(4, 5) = 1; 6 A(5, 6) = 5; 7 A(6, 7) = 2; 8 A(7, 8) = 3; 9 A(8, 9) = 5;
Prim算法实现:
1 A = A+A'; 2 A(A==0) = Inf; 3 P = zeros(1, 9); 4 P(1,1) = 1; 5 V = 1:9; 6 V_P = V - P; 7 link = zeros(8,2); 8 k=1; 9 while k<9 10 p = P(P~=0); 11 v = V_P(V_P~=0); 12 pv = min(min(A(p,v))); 13 [x, y] = find(A==pv); 14 for i=1:length(x) 15 if any(P==x(i)) && any(V_P==y(i))集合判断,关键! 16 P(1,y(i)) = y(i); 17 V_P = V - P; 18 link(k, :) = [x(i), y(i)]; 19 k = k+1; 20 break; 21 end 22 end 23 end
输出:
>> link link = 1 3 3 4 4 5 1 2 2 9 1 7 7 6 7 8
Kruskal算法实现:
1 A = sparse(A'); 2 A(A==0) = Inf; 3 B = sparse(9, 9); 4 link = graphallshortestpaths(B, 'directed', false); 5 while sum(sum(link)) == Inf%如果不连通,则和无穷大 6 ind = find(A==min(min(A))); 7 [x, y] = ind2sub(size(A), ind);%寻找最短边 8 for i=1:length(x) 9 if link(x(i), y(i))==Inf%判断是否连通,关键!! 10 B(x(i), y(i)) = A(x(i), y(i)); 11 A(x(i), y(i))=Inf;%取差集 12 end 13 end 14 link = graphallshortestpaths(B, 'directed', false); 15 end
输出:
B = (2,1) 2 (3,1) 1 (7,1) 2 (9,2) 1 (4,3) 1 (5,4) 1 (7,6) 2 (8,7) 3
所以结果是:
(算法实现写于2015-12-18)
下一步工作,用其他语言实现,复杂度分析,深入论证算法正确性。
另外,代码中使用了graphallshortestpaths函数,这是最短路径的问题。关于最短路径将在下一篇讲述。其实MATLAB有关于求求最小生成树的函数graphminspantree,关于这一套函数,将结合官网资料,以后做梳理。
1 A = sparse(A'); 2 >> graphminspantree(A) 3 ans = 4 (2,1) 2 5 (3,1) 1 6 (7,1) 2 7 (9,2) 1 8 (4,3) 1 9 (5,4) 1 10 (7,6) 2 11 (8,7) 3
如此,可直接求得最小生成树。