字符串-BM算法
问题说明
BM算法是一种字符串匹配算法,也就是存在两个字符串,用其中一个较短的字符串(称之为模式串)去匹配较长的字符串(待匹配串),看它是不是较长的字符串的子串。例如:
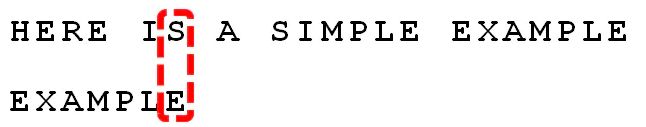
用EXAMPLE 来匹配是否为 HERE IS A SIMPLE EXAMPLE 的子串。
具体的方式如下:
首先,我们要了解两个概念:
(这里过于抽象可以先不看)
- 坏字符算法:在模式串向后移动的过程中让坏字符尽量匹配模式串中最后面的与坏字符相同的字符
- 好后缀算法:
具体的使用我们直接带到例子中看。
step 1
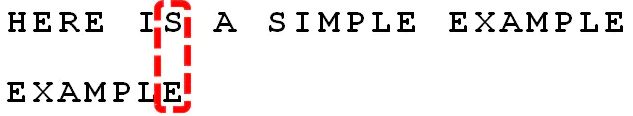
BM算法是基于后缀的比较方法,也就是每次比较都是从模式串最后面来与待匹配字符串比较。这里,可以看到,S 与 E匹配失败。此时,将S称作坏字符,这时候存在两种情况:
- 坏字符S在模式串中出现了;
- 坏字符串没有在模式串中出现;
这时候我们根据情况不同,采取不同的移动模式串的方式
这里设以下参数:
- P(S):匹配失败的位置,即坏字符S对应模式串中的E,而E在模式串中处于从左向右第6个位置(从0开始计数)
- L(S): 坏字符在模式串中出现的最靠右的位置(计算位置的方法和P(S)一样),若未出现则为-1,
由此,我们根据两种情况做出位移操作:
S h i f t = P ( S ) − L ( S ) Shift = P(S) - L(S) Shift=P(S)−L(S)
所以此时,模式串向右移动 S h i f t = P ( S ) − L ( S ) = 6 − ( − 1 ) = 7 Shift = P(S) - L(S) = 6 - (-1) = 7 Shift=P(S)−L(S)=6−(−1)=7个偏移量。
step 2

这里仍然满足坏字符算法,所以再次向右移动 P ( P ) − L ( P ) = 6 − 4 = 2 P(P) - L(P) = 6 - 4 = 2 P(P)−L(P)=6−4=2个偏移量。
step 3
- 模式串后面的 MPLE 与待匹配字符串中的 MPLE 匹配成功
- 模式串后面的 A 和待匹配字符串中的 I 匹配失败
这里,第二种情况符合坏字符的情况,计算位移数 S h i f t = P ( I ) − L ( I ) = 2 − ( − 1 ) = 3 Shift = P(I) - L(I) = 2 - (-1) = 3 Shift=P(I)−L(I)=2−(−1)=3
这里我们来定义第一种情况算法:
- 好后缀算法:此时,位移数 S h i f t = L − N Shift = L - N Shift=L−N
- LEN:模式串长度(从0开始计数)
- N: 模式串最后一个字符从右向左数第二次出现的位置,若只出现了一次,则N为-1
所以,这里好后缀算法的位移数 S h i f t = 6 − 0 = 6 Shift = 6 - 0 = 6 Shift=6−0=6
当同时存在坏字符情况和好后缀情况时 ,采用位移数最大的作为真正的位移。
step 3
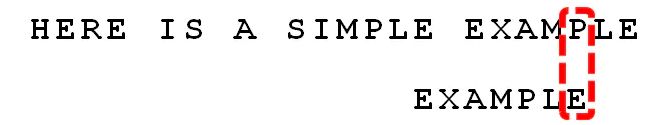
这里,使用坏字符算法,位移数为 S h i f t = 6 − 4 = 2 Shift = 6 - 4 = 2 Shift=6−4=2
step 4

这里,我们发现从右向左全部匹配成功,算法结束;
这里需要注意的是,当模式串向右移动的过程中要判断模式窜最右面的字符的位置是否已经超过待匹配的字符串的位置了。

