图的基本操作
1. 图的基本概念
图是由顶点集合及顶点间的关系组成的一种数据结构:G = (V, E),
顶点集合V = {x|x属于某个数据对象集}是有穷非空集合;
E = {(x,y)|x,y属于V}或者E = {
(x, y)表示x到y的一条双向通路,即(x, y)是无方向的;
Path(x, y)表示从x到y的一条单向通路,即Path(x, y)是有方向的。
图中结点称为顶点,第i个顶点记作vi。两个顶点vi和vj相关联称作顶点vi和顶点vj之 间有一条边,图中的第k条边记作ek,ek = (vi,vj)或
2. 图的分类
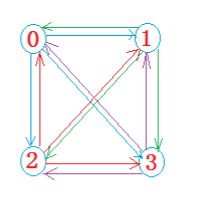
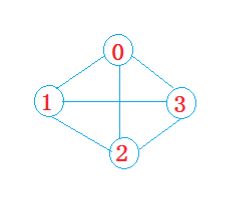
图分为有向图和无向图。
有向图(如左图):顶点对
无向图(如右图):顶点对(x, y)是无序的,顶点对(x,y) 称为顶点x和顶点y相关联的一条边,这条边没有特定方向,(x, y)和(y,x)是同一条边。无向边 (x, y)等于有向边
3. 图的基本性质
(1)邻接顶点:在无向图中G中,若(u, v)是E(G)中的一条边,则称u和v互为邻接顶点,并称边(u, v)依附于顶点u和v;
在有向图G中,若
(2)顶点的度:顶点v的度是指与它相关联的边的条数,记作deg(v)。
在有向图中,顶点的度等于该顶 点的入度(indev)与 出度(outdev)之和,即 dev(v) = indev(v) + outdev(v) ;
对于无向图,顶点的度等于该顶点的入度和出度,即dev(v) = indev(v) = outdev(v);
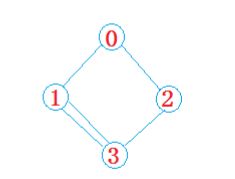
(3)路径:在图G = (V, E)中,若从顶点vi出发有一组边使其可到达顶点vj,则称顶点vi到顶点vj的顶点序列为从顶点vi到顶点vj的路径。例如左图:顶点0到顶点3的路径为{0,1,3};
(4)路径长度:对于不带权的图,一条路径的路径长度是指该路径上的边的条数,如左图:顶点0到3的路径长度为2;对于带权的图,一条路径的路径长度是指该路径上各个边权值的总和,如右图:顶点A到E的路径长度为75。
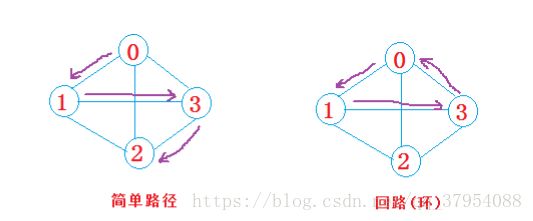
(5)简单路径与回路:若路径上各顶点v1,v2,v3,…,vm均不重复,则称这样的路径为简单路径(如左图)。若路 径上第一个顶点v1和最后一个顶点vm重合,则称这样的路径为回路或环(如右图)。
(6)子图:设图G = {V, E}和图G1 = {V1,E1},若V1属于V且E1属于E,则称G1是G的子图。
(7)连通图:在无向图中,若从顶点v1到顶点v2有路径,则称顶点v1与顶点v2是连通的。
如果图中任意一 对顶点都是连通的,则称此图为连通图。
任意N顶点的连通图有N-1条边。
(8)强连通图:在有向图中,若在每一对顶点vi和vj之间都存在一条从vi到vj的路径,也存在一条从vj到 vi的路径,则称此图是强连通图。
任意N顶点的强连通图有N条边。
(9)生成树:一个连通图的最小连通子图称作该图的生成树。有n个顶点的连通图的生成树有n个顶点和n-1条边。
4. 图的存储结构
邻接矩阵
(1)将所有顶点的信息组织成一个顶点表,然后利用一个矩阵来表示个顶点之间的邻接关系。 设图G = (V, E)包含n个顶点,则A的邻接矩阵是一个二维数组G.Edge[n][n]。
(2)无向图的邻接矩阵是对称的,第i行(列)元素之和,就是顶点i的度。
有向图的邻接矩阵则不一定 是对称的,第i行(列)元素之后就是顶点i 的出(入)度。
(3)利用邻接矩阵实现图的基本操作
template
class Graph
{
public:
Graph()
{}
Graph(const T* arr,const size_t& size)
{
_v.resize(size);
for (size_t i = 0; i < size; i++)
{
_v[i] = arr[i];
}
//动态开辟二维数组
_Edge.resize(size);
for (size_t i = 0; i < size; i++)
{
(_Edge[i]).resize(size);
}
}
size_t Getsign(const T& value)
{
int size = _v.size();
int index = 0;
for (index = 0; index < size; index++)
{
if (_v[index] == value)
return index;
}
return -1;
}
void Insert(const T& value1, const T& value2, const W&weight)
{
int index1 = Getsign(value1);
int index2 = Getsign(value2);
if (index1 != -1 && index2 != -1)
{
_Edge[index1][index2] = weight; //有向图
if (Isdirector) //无向图
_Edge[index2][index1] = weight;
}
}
int GetWeight(const T& value1, const T& value2)
{
int index1 = Getsign(value1);
int index2 = Getsign(value2);
if (index1 == -1 || index2 == -1)
{
cout << "顶点不存在!" << endl;
}
else
{
return _Edge[index1][index2];
}
}
//获取顶点的度
int Getdev(const T& value)
{
int size = _v.size();
int index = Getsign(value);
int dev = 0;
if (index != -1)
{
//无向图
for (size_t i = 0; i < size; i++)
{
if (_Edge[index][i] != 0)
dev++;
}
//有向图
if (!Isdirector)
for (size_t j = 0; j < size; j++)
{
if (_Edge[j][index] != 0)
dev++;
}
return dev;
}
return -1;
}
void showGraph()
{
size_t size = _v.size();
for (size_t i = 0; i < size; i++)
{
for (size_t j = 0; j < size; j++)
{
printf("%-2d ", _Edge[i][j]);
}
cout << " " << endl;
}
}
private:
vector _v; //图的顶点
vector > _Edge; //任意两个顶点的边的权值
}; 注:在使用邻接矩阵存储边时,如果是无向图资源浪费问题不大,但是对于有向图来说,若只有极少数边的话,即当e远远小于n^2时,空间浪费比较严重。
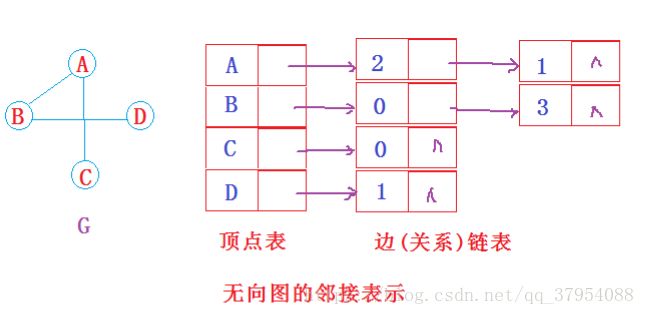
邻接表
(1)邻接表:使用数组表示顶点的集合,使用链表表示边的关系。
(2)无向图
无向图中同一条边在邻接表中出现了两次。 如果想知道顶点vi的度,只需要知道顶点vi边链表集合中结点的数目即可。
(3)有向图
有向图中每条边在邻接表中只出现一次。 与顶点vi对应的邻接表所含结点的个数,就是该顶点的出度,也称出度表。 要得到vi顶点的入度,必须检测其他所有顶点对应的边链表,看有多少边顶点的dst取值是i
(4)利用邻接表实现图的基本操作
template
struct GraphNode
{
GraphNode(const size_t& src,const size_t& dest,const W& weight)
:_src(src)
, _dest(dest)
, _weight(weight)
,_PNext(NULL)
{}
GraphNode* _PNext;
size_t _src; //起点下标
size_t _dest; //终点下标
W _weight; //边的权值
};
template
class Compare
{
typedef GraphNode * PNode;
public:
bool operator()(PNode Left, PNode Right)
{
return Left->_weight < Right->_weight;
}
};
template
class Graph
{
typedef GraphNode Node;
typedef Node* PNode;
public:
Graph(const T* arr, const size_t& size)
{
_v.resize(size);
_Edge.resize(size);
for (size_t i = 0; i < size; i++)
{
_v[i] = arr[i];
}
}
size_t Getsign(const T& value)
{
int size = _v.size();
int index = 0;
for (index = 0; index < size; index++)
{
if (_v[index] == value)
return index;
}
return -1;
}
void Insert(const T& value1, const T& value2,const W& weight)
{
int src = Getsign(value1);
int dest = Getsign(value2);
PNode Pcursrc = _Edge[src];
PNode Pcurdest = _Edge[dest];
//看当前边是否在邻接表中
/*while (Pcursrc)
{
if (Pcursrc->_dest == dest)
return;
Pcursrc = Pcursrc->_PNext;
}*/
//有向图
if (src != -1 && dest != -1)
{
PNode newNode = new Node(src,dest,weight);
newNode->_PNext = Pcursrc;
_Edge[src] = newNode;
if (Isdirector)//无向图
{
PNode newNode = new Node(src,dest,weight);
newNode->_PNext =Pcurdest;
_Edge[dest] = newNode;
}
}
}
int Getdev(const T& value)
{
int index = Getsign(value);
size_t size = _v.size();
PNode Pcur = _Edge[index];
int count = 0;
//无向图
while (Pcur != NULL)
{
count++;
Pcur = Pcur->_PNext;
}
if (!Isdirector)
{
for (size_t i = 0; i < size && i!=index; i++)
{
PNode pcur = _Edge[i];
while (pcur)
{
if (pcur->_dest == index)
count++;
}
}
}
return count;
}
int GetWeight(const T& value1, const T& value2)
{
int src = Getsign(value1);
int dest = Getsign(value2);
if (src != -1 && dest != -1)
{
PNode pcur = _Edge[src];
while (pcur)
{
if (pcur->_dest == dest)
return pcur->_weight;
pcur = pcur->_PNext;
}
}
return -1;
}
void showGraph()
{
size_t size = _v.size();
for (size_t i = 0; i < size; i++)
{
PNode pcur = _Edge[i];
while (pcur)
{
cout << _v[pcur->_src] << " "<<_v[pcur->_dest]<<" " << pcur->_weight << endl;
pcur = pcur->_PNext;
}
}
}
private:
vector _v; //顶点
vector _Edge; //存储边
};