本周算法题总结——中级算法专题(1~6 数组和字符串)
上班了,学了老久的Java居然写不了了,现在的方向用的语言主要是Python,所以之后算法题都用Python写(之后用go了,再用go).
学习期期间把剑指offer整本刷完了,不过代码和题解全写日报上了(主管:这家伙果然工作不饱和),之后有机会再整理一波.
<剑指offer>真的是本很好的书不仅应付面试,还有算法入门.
争取每天一题,周末写个总结.先从lc的中级题专题刷起吧.
1.三数之和

思路: 三个数字和为0,除非仨0,要不然就是就肯定至少一个与其他符号相反,这样就需要统计正负数,那排个序呗,然后双指针扫,不过需要仨数,那就用一个数字当桩,然后另外俩在左右两边,小于0则左指针右移,大右左…
不过需要注意不能有重复的,也就是说每次桩不能相同,然后同一个桩的情况下,两次数任意数字不能与上次相同(因为当两个数固定时,和0为的情况只有一种)
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
ans = []
if nums==None or len(nums)<3:
return ans
nums = sorted(nums)
for i in range(len(nums)-2):
if i!=0 and nums[i]==nums[i-1]:
continue
left = i+1
right = len(nums)-1
while left<right:
sum_ = nums[left]+nums[right]+nums[i]
if sum_==0:
ans.append([nums[i],nums[left],nums[right]])
left += 1
while left<len(nums) and nums[left]==nums[left-1]:
left += 1
right -= 1
else:
if sum_<0:
left += 1
else:
right -= 1
return ans
2.矩阵置零

思路: 常规思路很简单,遇到一个0标记当列的行和列,然后再读取行和列,哪些需要置为0,置0 就好,如果只能用一个常数的解决方案,就需要在原矩阵里处理.
将矩阵想象成一个表格,表格外层有个每一栏的名称,那么我们也阔以在每一"栏"外层记录该行/列应不应该置0,栏就用最外层担当(第0行/列),可是栏位也是原矩阵呀,所以就需要先记录第0行/列该不该全置0
class Solution(object):
def setZeroes(self, matrix):
"""
:type matrix: List[List[int]]
:rtype: None Do not return anything, modify matrix in-place instead.
"""
if matrix==None or len(matrix)==0 or matrix[0] == None or len(matrix[0])==0:
return
flagR = False
for i in matrix[0]:
if i==0:
flagR =True
break
flagC = False
for i in range(len(matrix)):
if matrix[i][0]==0:
flagC = True
break
for i in range(1,len(matrix)):
for j in range(1,len(matrix[0])):
if matrix[i][j]==0:
matrix[i][0] = 0
matrix[0][j] = 0
for i in range(1,len(matrix[0])):
if matrix[0][i]==0:
for j in range(1,len(matrix)):
matrix[j][i] = 0
for i in range(len(matrix)):
if matrix[i][0]==0:
tmp = matrix[i][0]
matrix[i] = [0]*len(matrix[0])
matrix[i][0] = tmp
if flagC:
for i in range(len(matrix)):
matrix[i][0] = 0
if flagR:
matrix[0] = [0]*len(matrix[0])
3.字母异位词
 思路: 顺序无关,那说明只要给定的字母出现的次数相同就是字母异位词了.且范围只有26个,长度为26的list足矣,数组中再嵌套个list存储有哪些异位词.也可以每个词的字母顺序排序作为顺序作为键.
思路: 顺序无关,那说明只要给定的字母出现的次数相同就是字母异位词了.且范围只有26个,长度为26的list足矣,数组中再嵌套个list存储有哪些异位词.也可以每个词的字母顺序排序作为顺序作为键.
class Solution(object):
def groupAnagrams(self, strs):
"""
:type strs: List[str]
:rtype: List[List[str]]
"""
ans = {}
for str_ in strs:
count = [0]*26
for c in str_:
count[ord(c)-ord('a')] += 1
count = str(count)
if count in ans:
ans[count].append(str_)
else:
ans[count] = [str_]
return ans.values()
4.无重复字符的最长子串
 思路: 滑动窗口呀,当出现重复的字母时,窗口的左端缩到重复字符上次出现的位置+1,右边的窗口一直往右扩张.这就需要使用一个啥玩意记录上次一某个字符出现的位置.可以用256长度的list(记录ascii码),当然用dict也阔以.
思路: 滑动窗口呀,当出现重复的字母时,窗口的左端缩到重复字符上次出现的位置+1,右边的窗口一直往右扩张.这就需要使用一个啥玩意记录上次一某个字符出现的位置.可以用256长度的list(记录ascii码),当然用dict也阔以.
class Solution(object):
def lengthOfLongestSubstring(self, s):
"""
:type s: str
:rtype: int
"""
mm = [-1]*256
start = 0
ans = 0
for i in range(len(s)):
c = s[i]
if mm[ord(c)]!=-1 and mm[ord(c)] >= start:
ans = max(ans,i-start)
start = mm[ord(c)]+1
mm[ord(c)] = i
return max(len(s)-start,ans)
5.最长的回文子串
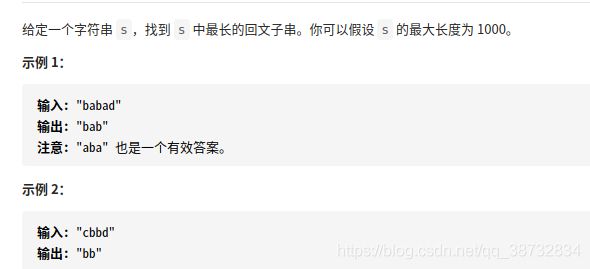
思路: 虽然动态规划不是最快的方法,但是俺还是想用动态规划,区间dp,
动归大多第一件事是思考子问题是怎样的,回文子串,它必然它左右边界各缩小1还是回文子串.
然后第二件事就是定义状态,根据子问题,就是从a~b的字符串是否为回文子串.dp[a][b]
第三件事转移方程:还是根据子问题, dp[a][b] = s[a]==s[b] && dp[a+1][b-1]
第四件事,初始化,即最简单的时候,该是怎样的,最简单的情况,长度为1的字符串必然是回文串,长度小于3的只要左右相等即可
第五件事状态压缩…这玩意压缩不了…
class Solution(object):
def longestPalindrome(self, s):
"""
:type s: str
:rtype: str
"""
dp = [[False]*len(s) for _ in range(len(s))]
# for i in range(len(dp)):
# dp[i][i] = True
end = 0
start_ = 0
for i in range(1,len(dp)+1):
for start in range(len(dp)-i):
flag = s[start]==s[start+i]
if i<3:
dp[start][start+i] = flag
else:
dp[start][start+i] = flag and dp[start+1][start+i-1]
if dp[start][start+i] and i>end-start_:
end = start+i
start_ = start
return s[start_:end+1]
6.递增的三元子序列
 思路:如果一直往后找,能够找到第三个较前面大的数,当然前提是需要找到第二个较前面一个数大的数,然后…好像有点套娃的味道,但是用动态规划,需要O(n^2)/O(NlogN)的时间复杂度,有点类似最大上升序列,然后当长度为3时,就行了.
思路:如果一直往后找,能够找到第三个较前面大的数,当然前提是需要找到第二个较前面一个数大的数,然后…好像有点套娃的味道,但是用动态规划,需要O(n^2)/O(NlogN)的时间复杂度,有点类似最大上升序列,然后当长度为3时,就行了.
还有一种方法,贪心的方法,首先尝试让当前的数字作为最小的数字,如果不行,尝试当中间的数字,还是不行,则说明找到了.
class Solution(object):
def increasingTriplet(self, nums):
"""
:type nums: List[int]
:rtype: bool
"""
num1 = sys.maxsize
num2 = num1
for i in nums:
if i<=num1:
num1 = i
elif i<=num2:
num2 = i
else:
return True
return False