无向图1----图的邻接表数组表示以及DFS、BFS搜索算法实现
图是由一组顶点以及一组能够将两个顶点相连的边组成的。
图数据结构的核心概念:
顶点 边 连通性 二分性 环 有向性
图的表示方法主要由邻接矩阵和邻接表数组方法。
邻接表数组数据结构
将图的顶点依次编号0,1,2,..V-1,假定顶点总数为V,则分配V数组大小,其中每个元素为一个链表,用来存储与该顶点相邻的节点链表。
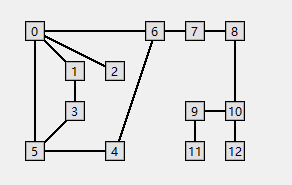
则上图可以表示如下所示:
0: 6--->5--->2--->1
1: 3--->0
2: 0
3: 5--->1
4: 6--->5
5: 4--->3--->0
6: 7--->4--->0
7: 8--->6
8: 10--->7
9: 11--->10
10: 12--->9--->8
11: 9
12: 10对于邻接表数组,其基本为数组元素,数组每个元素为一个链表,保存所有与该顶点相邻的顶点,并且顶点的保存顺序是可以任意的,即同一张图得到的邻接表数据结构可能不同,可以使用List来存储,这里为了强调邻接表元素的无序性,使用背包Bag数据结构来存储邻接表。
背包Bag数据支持添加以及遍历操作,不支持删除,并且背包中的元素添加顺序是不重要的。
背包Bag使用链式节点Node来实现,类似于LinkedList。
背包Bag数据结构
//背包数据结构 支持数据存储添加遍历操作
//不支持删除以及查找操作
//元素添加顺序不重要
public class Bag- implements Iterable
- {
private Node
- first;
private int n;
private static class Node
- {
private Item item;
private Node
- next;
}
public Bag(){
first = null;
n = 0;
}
public boolean isEmpty(){
return first == null;
}
public int size(){
return n;
}
public void add(Item item){
Node
- oldfirst = first;
first = new Node<>();
first.item = item;
first.next = oldfirst;
n++;
}
@Override
public Iterator
- iterator() {
return new ListIterator
- (first);
}
private class ListIterator
- implements Iterator
- {
private Node
- current;
public ListIterator(Node
- first) {
current = first;
}
@Override
public void remove() {
throw new UnsupportedOperationException();
}
@Override
public boolean hasNext() {
return current != null;
}
@Override
public Item next() {
if(!hasNext()) throw new NoSuchElementException();
Item item = current.item;
current = current.next;
return item;
}
}
public static void main(String[] args) {
Bag
bag = new Bag<>();
for(int i=0; i<10; i++){
bag.add(i);
}
Iterator it = bag.iterator();
while(it.hasNext()){
System.out.println(it.next());
}
}
}
图的数据结构实现
使用Graph来表示图数据结构,其中主要属性有顶点数,边数以及连接表数组,数组的每一个元素为一个背包Bag。
//图数据结构表示
//利用SWT来表示一张图
//顶点 边 度数 连通图
public class Graph {
//顶点数
private final int V;
//边数
private int E;
//邻接表
private Bag[] adj;
} 当向其中加入一条边v--w时,需要向其中添加两次adj[v].add(w) adj[w].add(v)
//添加一条边
public void addEdge(int v, int w){
adj[v].add(w);
adj[w].add(v);
E++;
}可以快速获取某个顶点相邻的顶点列表以及求解某一个顶点的度数
//某一个节点的相邻节点
public Iterable adj(int v){
return adj[v];
}
//某一个顶点度数
public int degree(int v){
return adj[v].size();
} DFS,BFS是图的搜索算法,其基本思路:
/*
* 图搜索算法思路
* 将起点加入数据结构中,重复一下步骤直到数据结构为空
* 取出数据结构中的数据,标记数据
* 将与该数据所有相邻未标记节点加入到数据结构中
* 深度优先数据结构使用栈 每次取出最近的节点
* 广度优先使用队列,每次取出最远的节点
* */
DFS深度优先搜索
利用递归思想,当访问某一个节点时,遍历该节点的相邻节点,如果某个节点没有被访问过,则继续对该节点调用dfs,遍历该节点的相邻节点,如果某个节点相邻节点都已访问过,则返回到该节点的上一个节点,对于上一个节点调用dfs
使用一个数组marked来表示每个节点是否被访问过
private void dfs(Graph g, int s) {
arr.add(s);
marked[s] = true;
count++;
for(int v : g.adj(s)){
if(!marked(v))
dfs(g, v);
}
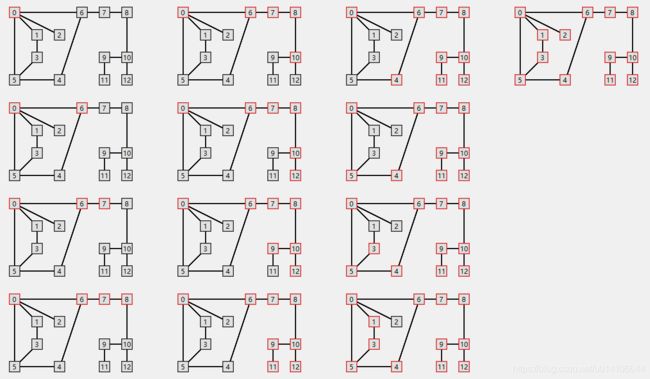
}DFS路径SWT演示,保存DFS对于图顶点访问顺序,然后依次绘制DFS是如何完成图的遍历的。
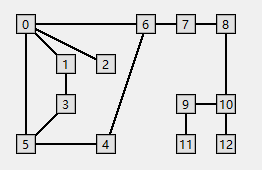
对于下图,从顶点0开始深度优先搜索
其具体的搜索路径如下: 顶点访问顺序 [0, 6, 7, 8, 10, 12, 9, 11, 4, 5, 3, 1, 2]
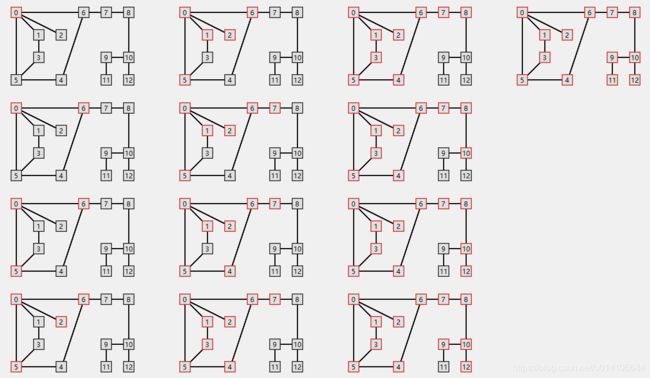
BFS广度优先搜索
当搜索到某一个顶点时,依次遍历该顶点所有相邻顶点,并将相邻顶点加入到队列中,如果该顶点所有相邻顶点都已经访问过,则从队列中取出一个顶点,继续进行该过程。
private void bfs(Graph g, int s) {
Queue q = new LinkedList<>();
marked[s] = true;
q.add(s);
while(!q.isEmpty()){
int v = q.poll();
arr.add(v);
for(int w : g.adj(v)){
if(!marked[w]){
marked[w] = true;
q.add(w);
}
}
}
} 对于上图进行BFS搜索如下: 顶点访问顺序 [0, 6, 5, 2, 1, 7, 4, 3, 8, 10, 12, 9, 11]
BFS实现从起始点由近到远来访问图数据结构,即依次访问距离起始点路径长度为0,1,..的顶点。
图结构:
邻接表数组表示如下:
0: 6--->5--->2--->1
1: 3--->0
2: 0
3: 5--->1
4: 6--->5
5: 4--->3--->0
6: 7--->4--->0
7: 8--->6
8: 10--->7
9: 11--->10
10: 12--->9--->8
11: 9
12: 10DFS搜索顶点访问顺序为: dfs = [0, 6, 7, 8, 10, 12, 9, 11, 4, 5, 3, 1, 2]
BFS顶点访问顺序为: bfs = [0, 6, 5, 2, 1, 7, 4, 3, 8, 10, 12, 9, 11]
SWT代码位置:https://github.com/ChenWenKaiVN/TreeSWT/blob/master/src/com/swt/GraphSWT.java