数据结构与算法——十大排序算法(总结向)
文章目录
- 0 十大排序算法(总结向)
- 0.1 排序性能的衡量方法
- 0.2 九大排序算法的性能分析
- 1 起泡排序
- 1.1 算法步骤
- 1.2 动图演示
- 1.3 代码实现
- 2 选择排序
- 2.1 算法步骤
- 2.2 动图演示
- 2.3 代码实现
- 3 插入排序
- 3.1 算法步骤
- 3.2 动图演示
- 3.3 代码实现
- 4 希尔排序
- 4.1 算法步骤
- 4.2 动图演示
- 4.3 代码实现
- 5 归并排序
- 5.1 算法步骤
- 5.2 图片演示
- 5.3 代码实现
- 6 快速排序
- 6.1 算法步骤
- 6.2 图片演示
- 6.3 代码实现
- 7 堆排序
- 7.1 算法步骤
- 7.2 动图演示
- 7.3 代码实现
- 8 桶排序
- 8.1 算法步骤
- 8.2 图片演示
- 8.3 代码实现
- 9 基数排序
- 9.1 算法步骤
- 9.2 动图演示
- 9.3 代码实现
- 10 计数排序
- 10.1 算法步骤
- 10.2 动图演示
- 10.3 代码实现
0 十大排序算法(总结向)
在计算机科学与数学中,一个排序算法(Sorting algorithm)是一种能将一串数据按照特定排序方式进行排列的一种算法。
0.1 排序性能的衡量方法
-
时间复杂度 一个排序的理想性能是O(n),实际上至少需要O(nlogn)
-
空间复杂度 内存的使用量
-
稳定性 稳定排序算法使原本有相等键值的记录维持相对次序
0.2 九大排序算法的性能分析
| 名称 | 数据对象 | 稳定性 | 时间复杂度 | 空间复杂度 |
|---|---|---|---|---|
| 起泡排序 | 数组 | 好 | O(n^2) | O(1) |
| 选择排序 | 数组/链表 | 不好/好 | O(n^2) | O(1) |
| 插入排序 | 数组/链表 | 好/好 | O(n^2) | O(1) |
| 希尔排序 | 数组 | 不好 | O(nlogn) ~ O(n^2) | O(1) |
| 归并排序 | 数组/链表 | 好/好 | O(nlogn) | O(1) |
| 快速排序 | 数组 | 不好 | O(nlogn) | O(1) |
| 堆排序 | 数组 | 不好 | O(nlogn) | O(1) |
| 桶排序 | 数组/链表 | 好/好 | O(n + k) | O(n + k) |
| 基数排序 | 数组/链表 | 好/好 | O(n x k) | O(n + k) |
| 计数排序 | 数组/链表 | 好/好 | O(n + k) | O(n + k) |
1 起泡排序
1.1 算法步骤
从低到高,判断A[ i ]与A[ i + 1 ],若A[ i ] > A[ i + 1 ],则交换
重复上述操作,直到没有逆序对(因为每次最大的都能移到最后一位,所以n次一定能保证完全有序)
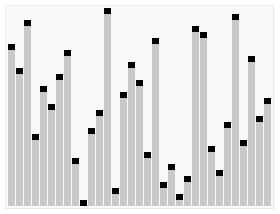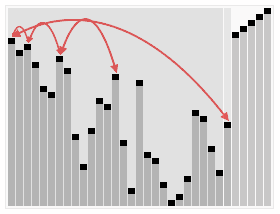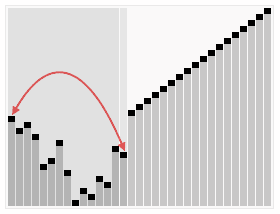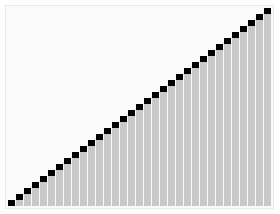
1.2 动图演示
1.3 代码实现
以下九种排序算法都是在这个框架下进行实现与测试
#include 2 选择排序
2.1 算法步骤
从无序堆中,找出最大(小)值,将其插入到无序堆的最后位置之后一位(最前位置的前一位)
重复以上操作,直到排序完毕(n次)
2.2 动图演示
2.3 代码实现
//选择排序
void selectionSort( int* arr, int len ){
for( int i = 0; i < len; ++i ){//n个元素依次处理
int min = i;
for( int j = i + 1; j < len; ++j){
if( arr[ j ] < arr[ min ])
min = j;//记录未排序中最小值位置
}
swap( arr[i], arr[min]);
}
}//29 17 34 22 50 21 60 61 62 1 72
3 插入排序
3.1 算法步骤
从头到尾扫描未排序序列,将扫描到的每个元素插入到有序序列的适当位置(遇到第一个小于等于该元素的后面位置)
3.2 动图演示
3.3 代码实现
//插入排序
void insertionSort( int* arr, int len ){
for( int i = 1; i < len; ++i ){
int key = arr[i];
int j = i -1;//当前无序序列的前一个元素位置
while( j >=0 && arr[j] > key){//插入到遇到的第一个小于等于key的元素后面
arr[ j + 1 ] = arr[ j ];
--j;
}
arr[ j + 1 ] = key;
}
}//1 17 21 22 29 34 50 60 61 62 72
4 希尔排序
4.1 算法步骤
基本思想:先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录"基本有序"时,再对全体记录进行依次直接插入排序。
算法步骤:
选择一个增量序列 t1,t2,……,tk,其中 ti > tj, tk = 1;
对序列进行k趟排序,每趟根据ti将序列分为若干长度为m的子序列,对子序列进行插入排序
4.2 动图演示
4.3 代码实现
//希尔排序
void shellSort( int* arr, int len ){
int h = 1;
while( h < len/3){
h = 3*h + 1;
}
while( h >= 1){
for( int i = h; i < len; ++i)//h是希尔序列的值
for( int j = i; j >= h && arr[ j ] < arr[ j - h] ; j -= h)
swap( arr[ j ], arr[ j-h ]);
h = h / 3;
}
}
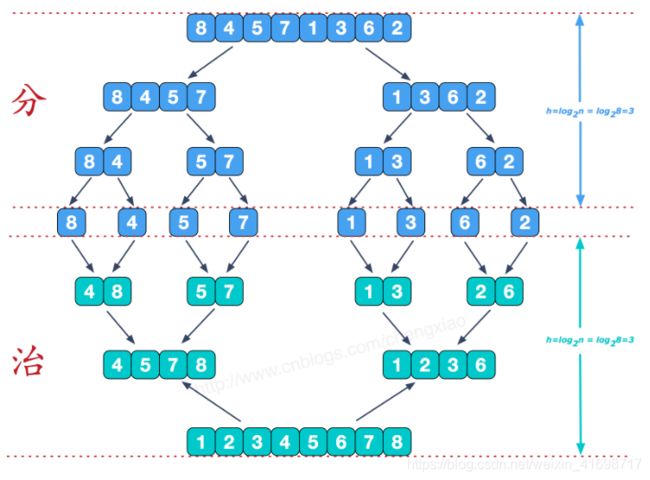
5 归并排序
5.1 算法步骤
基本思想:自上而下的递归,自下而上的迭代
1. 申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列;
2. 设定两个指针,最初位置分别为两个已经排序序列的起始位置;
3. 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置;
4. 重复步骤 3 直到某一指针达到序列尾;
5. 将另一序列剩下的所有元素直接复制到合并序列尾
5.2 图片演示
5.3 代码实现
//归并排序
void merge( int* A, int lo, int mi, int hi){
int* A1 = A + lo;
int lb = mi - lo;
int* B1 = new int[lb];//前子向量B1[0,lb) = A[lo,mi)
for( int i = 0; i < lb; ++i ) B1[i] = A1[i];
int lc = hi - mi; int* C1 = A + mi;//后子向量C1[0, lc) = A[mi, hi)
for( int i = 0, j = 0, k = 0; ( j < lb )||( k < lc );){
if((j < lb )&&(!(k < lc)||( B1[j] <= C1[k]))) A1[i++] = B1[j++];
if((k < lc )&&(!(j < lb)||( C1[k] < B1[j]))) A1[i++] = C1[k++];
}
delete [] B1;
}
void mergeSort( int* arr, int lo, int hi){
if( hi - lo < 2 ) return;//分
int mi = ( lo + hi ) / 2;
mergeSort( arr, lo, mi);
mergeSort( arr, mi, hi);
merge( arr, lo, mi, hi);//合
}
6 快速排序
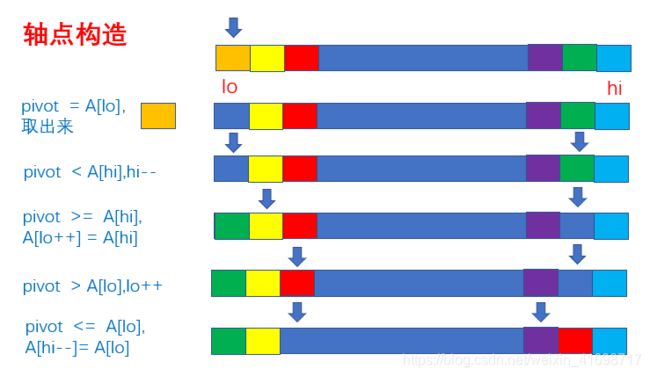
6.1 算法步骤
1. 从数列中挑出一个元素,称为 "基准"(pivot);
2. 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
3. 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序;
6.2 图片演示
6.3 代码实现
//partition函数,选取节点
int partition( int* A, int lo, int hi ){
swap( A[lo], A[ lo + rand()%( hi - lo + 1 )]);
int pivot = A[lo];
while( lo < hi ){
while( lo < hi )
if( pivot < A[hi])//大于pivot情况下
hi--;//向左扩展右子向量
else
{ A[lo++] = A[hi]; break;}//归入左子向量
while( lo < hi )
if( A[lo] < pivot )//小于pivot情况下
lo++;//向右扩展左子向量
else
{ A[hi--] = A[lo]; break;}//归入右子向量
}
A[lo] = pivot;
return lo;
}
//快速排序
void quickSort( int* A, int lo, int hi ){
if( hi - lo < 2 ) return;
int mi = partition( A, lo, hi - 1 );
quickSort( A, lo, mi );
quickSort( A, mi + 1, hi );
}
7 堆排序
7.1 算法步骤
1. 创建一个堆 H[0……n-1];
2. 把堆首(最大值)和堆尾互换;
3. 把堆的尺寸缩小 1,并调用 shift_down(0),目的是把新的数组顶端数据调整到相应位置;
4. 重复步骤 2,直到堆的尺寸为 1
7.2 动图演示
7.3 代码实现
//下滤
void percolateDown( int* arr, int lo, int hi ){
int dad = lo;
int son = 2*dad + 1;
while( son < hi ){
if( (son + 1 < hi) && (arr[ son ] < arr[ son + 1 ]))//先取son中较大者
son++;
if(arr[dad] > arr[son])
return;
else{//若dad不是最大的,下滤
swap( arr[dad], arr[son]);
dad = son;
son = 2*dad + 1;
}
}
}
//堆排序
void heapSort( int* arr, int len ){
//建堆
for( int i = len/2 -1; i >= 0; --i){
percolateDown( arr, i, len -1);
}
//交换
for( int i = len - 1; i > 0; --i){
swap( arr[0], arr[i]);
percolateDown( arr, 0, i );
}
}
8 桶排序
8.1 算法步骤
1. 构造元素为列表的桶
2. 将各个元素根据散列值放到各个桶的合适位置
3. 对各个有序的桶进行汇合
4. 将汇合的列表放入原数组中
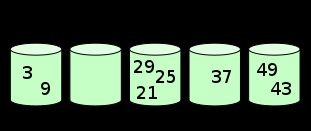
8.2 图片演示
8.3 代码实现
//桶排序
struct ListNode{
explicit ListNode(int i=0):mData(i),mNext(NULL){}
ListNode* mNext;
int mData;
};
ListNode* insert(ListNode* head,int val){
//列表插入,将val插入到列表合适的位置(大于val的节点的前面或者最后)
//返回头节点
ListNode dummyNode;
ListNode *newNode = new ListNode(val);
ListNode *pre,*curr;
dummyNode.mNext = head;//head是当前头节点
pre = &dummyNode;//这里不是引用,而是取地址
curr = head;
while(NULL!=curr && curr->mData<=val){
pre = curr;
curr = curr->mNext;
}
newNode->mNext = curr;
pre->mNext = newNode;
return dummyNode.mNext;
}
ListNode* Merge(ListNode *head1,ListNode *head2){
//将head1和head2汇合,返回汇合后列表的头节点
ListNode dummyNode;
ListNode *dummy = &dummyNode;
//汇合
while(NULL!=head1 && NULL!=head2){
if(head1->mData <= head2->mData){
dummy->mNext = head1;
head1 = head1->mNext;
}else{
dummy->mNext = head2;
head2 = head2->mNext;
}
dummy = dummy->mNext;
}
if(NULL!=head1) dummy->mNext = head1;
if(NULL!=head2) dummy->mNext = head2;
return dummyNode.mNext;
}
void BucketSort(int arr[], int n){
vector<ListNode*> buckets(BUCKET_NUM,(ListNode*)(0));
for(int i=0;i<n;++i){
//根据散列值放入到桶并插入到合适位置
int index = arr[i]/BUCKET_NUM;
ListNode *head = buckets.at(index);
buckets.at(index) = insert(head,arr[i]);
}
ListNode *head = buckets.at(0);
for(int i=1;i<BUCKET_NUM;++i){
//各个桶里的列表汇合
head = Merge(head,buckets.at(i));
}
for(int i=0;i<n;++i){
//重新放到数组中
arr[i] = head->mData;
head = head->mNext;
}
}
9 基数排序
9.1 算法步骤
1. 计算最大位数,即循环次数
2. 为每个桶分配元素数量(避免使用复杂的数据结构),从上往下依次插入(保证后续的有序)
3. 重复上一步达循环次数
9.2 动图演示
9.3 代码实现
//基数排序
int maxbit(int data[], int n) //辅助函数,数据的求最大位数
{
int maxData = data[0]; ///< 最大数
/// 先求出最大数,再求其位数,这样有原先依次每个数判断其位数,稍微优化点。
for (int i = 1; i < n; ++i)
{
if (maxData < data[i])
maxData = data[i];
}
int d = 1;
int p = 10;
while (maxData >= p)
{
//p *= 10; // Maybe overflow
maxData /= 10;
++d;
}
return d;
}
void radixsort(int data[], int n) //基数排序
{
int d = maxbit(data, n);//求最大位数
int *tmp = new int[n];
int *count = new int[10]; //计数器
int i, j, k;
int radix = 1;
for(i = 1; i <= d; i++) //进行d次排序
{
for(j = 0; j < 10; j++)
count[j] = 0; //每次分配前清空计数器
for(j = 0; j < n; j++)
{
k = (data[j] / radix) % 10; //统计每个桶中的记录数
count[k]++;
}
for(j = 1; j < 10; j++)
count[j] = count[j - 1] + count[j]; //将tmp中的位置依次分配给每个桶
for(j = n - 1; j >= 0; j--) //将所有桶中记录依次收集到tmp中,从后往前以保证顺序
{
k = (data[j] / radix) % 10;
//count[k]第一轮循环时等于n
tmp[count[k] - 1] = data[j];
count[k]--;
}
for(j = 0; j < n; j++) //将临时数组的内容复制到data中
data[j] = tmp[j];
radix = radix * 10;
}
delete []tmp;
delete []count;
}
10 计数排序
- 基数排序:根据键值的每位数字来分配桶;
- 计数排序:每个桶只存储单一键值;
- 桶排序:每个桶存储一定范围的数值;
10.1 算法步骤
1. 为每个桶分配元素数量,给临时向量分配位置
2. 从上到下依次插入(注意要减一,避免越界)
3. 将临时向量转移到原数组中
10.2 动图演示
10.3 代码实现
//计数排序
void countingSort( int arr[], int n){
vector<int> count( 100, 0 );//排序元素值为0到100的数组
vector<int> newvec( n, 0 );
//为各个桶计数
for( int j = 0; j < n; ++j ){
count[ arr[j] ] ++;
}
//给每个元素分配位置
for( int i = 1; i < 100; ++i ){
count[i] = count[i-1] + count[i];
}
//将元素放入newvec中
for( int j = n - 1 ; j >= 0; --j ){
newvec[ count[ arr[j] ] - 1 ] = arr[j];
//这里一定注意count的数值要减一,否则就超出数组边界了
count[ arr[j] ]--;
}
//将临时向量中的元素复制到原数组中
for( int j = 0; j < n; ++j )
arr[j] = newvec[j];
}