【我的区块链之路】- 谈一谈拜占庭问题的解及PBFT(拜占庭容错)
首先,我们来说一说什么是拜占庭问题。
【转载请标明出处】:https://blog.csdn.net/qq_25870633/article/details/81990517
【问题由来】
拜占庭的n个将军围攻敌人,n个将军包围着敌人,忠诚的将军希望通过某种协议达成某个命令的一致(比如约定某个时间一起进攻)。但其中一些背叛的将军会通过发送错误的消息阻挠忠诚的将军达成命令上的一致。如果同时发起进攻的将军数量少于m个,那么不足以歼灭敌人,反而容易被敌人全部歼灭。怎样做才能保证有多于m个将军在同一时间一起发起进攻?
【注意】:拜占庭问题是建立在通信信道可信的基础上的(即: 传输过程中,数据不会被窃取的情况下)
【问题实质】:
一群将军想要实现某一个目标(一致进攻或者一致撤退),但是单独行动或少于某个数目行动是行不通,必须合作, 达成共识;由于叛徒的存在,将军们不知道应该如何达到一致。这里“一致性”才是拜占庭将军问题探讨的内容。
“拜占庭将军问题”模型中,对于将军们(节点)有两个默认的假设:
1、 所有忠诚的将军收到相同的命令后,执行这条命令得到的结果一定是相同的;
2、 如果命令是正确的,那么所有忠诚的将军必须执行这条命令。
【提出假设】:
我们考虑4个将军的情况【为什么是4个而不是5个之类的,后面我们会讲】,同时假设4个将军中最多只有1个背叛者。当4个将军A、B、C、D把敌人包围了之后,必须协商一个统一的时间去发起进攻。
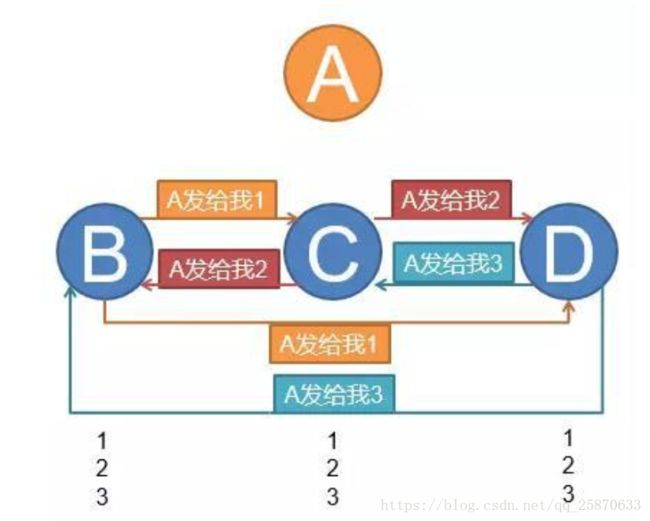
假设A为忠诚的:A将军派出了3个传令兵,分别告诉B、C、D将军,下午1点准时发起进攻。到了下午1点,A、C、D三个将军发起了进攻,歼灭了敌人,同时他们三个发现B是背叛的。虽然B背叛了,但是对最终任务没有影响。
假设A是背叛的:会发生什么情况?A派出3个传令兵,分别告诉B、C、D将军在下午1点、2点、3点发起进攻。于是,到了下午1点,B将军去攻击敌人,由于寡不敌众,全军覆没;2点,C将军全军覆没;3点,D将军全军覆没。
所以会有两种情况,
【一】:消息的发起者是忠诚的
【二】:消息的发起者是背叛者
问题解决的核心是,每一个将军接收到消息后都需要对消息的真实性做判断,如何做?(用共识算法做,怎么做?下面慢慢来说。。。)
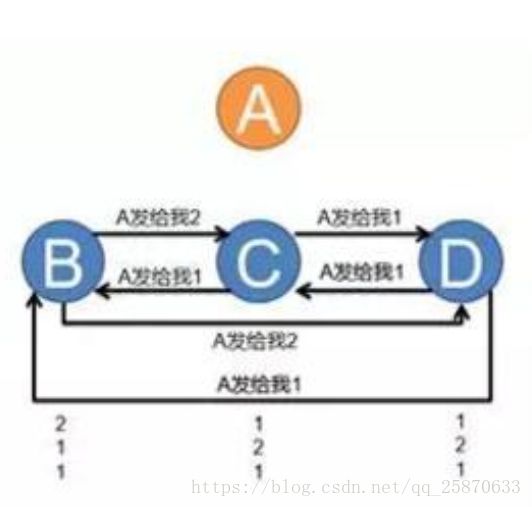
当A为叛徒时,可能会导致两种结果: 【B、C、D 都会在接收到A的消息后,相互访问A给其他人的答案。】
(当A只对其中一个说了真话,其他人说了不一样的假话,则全部节点都不进攻)
(当A只对其中一个人说了假话,则忠诚节点们都会自己通过相互访问A的消息来决定进攻时机)
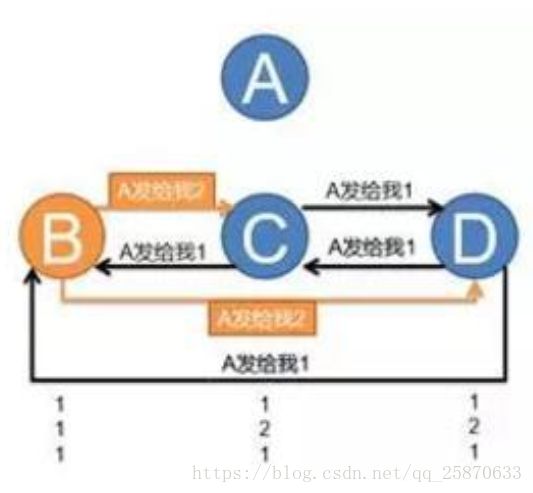
如果,发送者A和其他2个节点是忠诚的,而B是背叛者时:
(通过相互访问C、D节点可以自行判断出正确的答案,从而正确的和A一起发起进攻)
【解决拜占庭问题的算法】:PBFT (拜占庭容错算法)
PBFT算法的核心理论是:n>=3f+1;n 是系统中的总节点数,f 是允许出现故障的节点数。换句话说,如果这个系统允许出现f个故障,那么这个系统必须包括n个节点,才能解决故障。
那么为什么这么说呢?
理论的推导过程:
假设总数N个节点, f个故障节点,那么必须接收到N-f个消息应答(即 没有故障的节点的全部应答),就能够判断出结果(因为故障节点可能不发送应答)。N-f个应答中有f个可能是假的(故障节点发出的)【其中这句话最为奇妙,但是确实一个假设,因为可能有网络延迟等等,我们可以认为,作假的节点和真正故障的节点的数目是相等的,这句话值得慢慢体会,为什么作假节点被认为是f而不是 2f、3f等等,因为我们需要把有问题的节点的容忍度最大化 (系统需要稳定,肯定需要对有问题的节点做最大容忍),即就是 故障节点数目 == 作假节点数目,无论真实数目那边大,我们f 就是取了最大的那边的数值】,所以真实的是N-f-f,且 少数服从多数,及剩余的真实的应答大于有问题的应答, 即N-f-f > f ==> N > 3f。
所以: N_min = 3f + 1
当然下面我们也可以借助推理来一步步推导出来:
假设 n 为系统总节点数,m 为作假/故障节点数
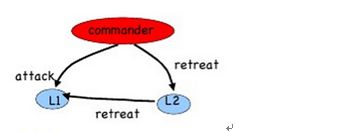
1) m = 1,n = 3 的情形: n=3,意味着一个司令发送命令给两个副官,m=1意味着他们中有一个叛徒。 首先考虑司令忠诚而副官2是叛徒的情况。
(m=1,n=3中司令忠诚而副官2是叛徒的情形)
司令把进攻命令传给了两个副官1和副官2,但是由于副官2为了不让他们达成一致,将司令的命令改成了撤退。那对于副官1来说,他应该如何判断?L1 无法知道是司令是叛徒还是副官2是叛徒,从而无法判断。
如果,司令为叛徒:
( m=1,n=3中司令是是叛徒的情形)
如果司令是叛徒,两个副官忠诚,司令会发送两个不同的命令。当两个副官对照命令时,他们又凌乱了,无法判断司令是叛徒或者对方是叛徒,从而又无法判断。
【结论】:总节点只有3个时,是无法动态容错的。
(2)m =1,n =4的情形: n=4,意味着一个司令发送命令给三个副官,m=1意味着他们中有一个叛徒。 首先考虑司令忠诚而副官3是叛徒的情况。
(m=1,n=4中司令忠诚而副官3是叛徒的情形)
倘若司令给各副官发送的消息都是进攻(A);之后,叛徒副官3给副官1和副官2说他收到的消息是撤退(R)。那么对于副官1(或副官2)来说,他综合司令、副官3和副官2(或副官1)后得到的消息向量都将会是(A,A,R),最终会采用 A。
如果,司令为叛徒:
假设叛徒司令会给三个副官发送的信息是(x,y,z)。之后,三位忠诚的副官将会交换他们收到的信息。对于副官1,他综合司令、副官2和副官3后得到的消息向量将会是(x,y,z),可以发现对于其他两个忠实的副官,他们得到的消息向量也将是(x,y,z)。不管x,y,z如何变化,但对于三人来说都是一样的,所以三个副官将会采用一致的行动,即:本次指令全部作废。
【结论】:n >= 3m + 1是可以容错的
PBFT(拜占庭容错)
基于拜占庭将军问题,一致性的确保主要分为这三个阶段:预准备(pre-prepare)、准备(prepare)和确认(commit)。流程如下图所示:
![]()
其中C为发送请求端,0、1、2、3为服务端,3为宕机的服务端,具体步骤如下:
1. Request:请求端C发送请求到任意一节点,这里是 0
2. Pre-Prepare:服务端0 收到C的请求后进行广播,扩散至1、2、3
3. Prepare:1、2、3收到后记录并再次广播,1 -> 0、2、3,2 -> 0、1、3,3因为宕机无法广播
4. Commit:0、1、2、3节点在Prepare阶段,若收到超过一定数量的相同请求,则进入Commit阶段,广播Commit请求
5.Reply (答复):0、1、2、3节点在Commit阶段,若收到超过一定数量的相同请求,则对C进行答复
6. 客户端等待来自不同节点的响应,若有 m+1 个相同的响应结果,则为本次运算的结果
根据上述流程,在 N ≥ 3F + 1 的情況下一致性是可能解決,N为总计算机数,F为有问题的计算机总数
N=4 F=0 时:
| 得到数据 | 最终数据 | |
| A | 1 1 1 1 | 1 |
| B | 1 1 1 1 | 1 |
| C | 1 1 1 1 | 1 |
| D | 1 1 1 1 | 1 |
N=4 F=1 时:
| 得到数据 | 最终数据 | |
| A | 1 1 1 0 | 1 |
| B | 1 1 0 1 | 1 |
| C | 1 0 1 1 | 1 |
| D | 0 1 1 1 | 1 |
N=4 F=2 时:
| 得到数据 | 最终数据 | |
| A | 1 1 0 0 | NA |
| B | 1 0 0 1 | NA |
| C | 0 0 1 1 | NA |
| D | 0 1 1 0 | NA |
由此可以看出,拜占庭容错能够容纳将近1/3的错误节点误差
到此,我们的拜占庭问题,及拜占庭容错算法就讲解完毕了。。