基于HMM的中文分词
隐马尔可夫模型(HMM)在中文分词中的应用
隐马尔可夫模型的详细解释
隐马尔可夫模型的一些范例介绍
隐马尔可夫模型中有两个序列,一个是状态序列,另一个是观测序列,其中状态序列是隐藏的。用具体的例子来解释。
假设一个房间内有N个装有球的盒子,在这些盒子中分别有M种不同颜色的球,我根据某一个概率分布(初始概率分布,在中文分词中就是一句话中第一个字符对应的状态概率)随机地选取一个初始的盒子,从中根据不同颜色的球的概率分布(发射概率,在中文分词中就是每一个字对应的状态概率),随机选择出一个球,然后我将这个球拿给房间外的你看。这个时候你能看到的就只是不同颜色的球的序列(观测序列),我选择的盒子的序列(状态序列)你是不知道的。
训练阶段参数估计
一个HMM可以由下面几个部分组成:
(1)模型中的状态数量N(上例中盒子的数量)
在中文分词中一般只有4个状态:STATES={‘B’,‘M’,‘E’,‘S’},例如:小明是中国人,对应的状态序列就是:B,E,S,B,M,E
(2)从每个状态可能输出的不同符号的数目M(上例中不同颜色球的个数)
在中文分词中就是对应每一个字符
在中文分词中就是状态序列STATES={‘B’,‘M’,‘E’,‘S’}的转移概率,这个状态概率矩阵是在训练阶段参数估计中得到。在中文分词中状态转移矩阵是一个4*4的矩阵,我在实验中是通过统计训练数据中状态转移的频数确定矩阵,为了确保![]() ,需要对频数矩阵除以对应每一行状态的统计数,即A[key0][key1]/count(key0),为了保证数据的精度,我这里取了对数,并且以字典输出方便查看。
,需要对频数矩阵除以对应每一行状态的统计数,即A[key0][key1]/count(key0),为了保证数据的精度,我这里取了对数,并且以字典输出方便查看。
{'B': {'B': -3.14e+100, 'M':-1.9594399657636383, 'E': -0.15191340104766693, 'S': -3.14e+100},
'M': {'B': -3.14e+100, 'M':-1.0983633205740504, 'E': -0.40558961540346977, 'S': -3.14e+100},
'E': {'B':-0.78182902092047468, 'M': -3.14e+100, 'E': -3.14e+100, 'S':-0.62312924475978682},
'S': {'B': -0.74289298827998818,'M': -3.14e+100, 'E': -3.14e+100, 'S': -0.81330579119502522}}
可以看到对应状态‘B’后面只能接‘M’和‘E’;状态‘M’后面只能接‘M’和‘E’;状态‘E’后面只能接‘B’和‘S’;状态‘S’后面只能接‘B’和‘S’。
在中文分词中发射概率指的是每一个字符对应状态序列STATES={‘B’,‘M’,‘E’,‘S’}中每一个状态的概率,通过对训练集每个字符对应状态的频数统计得到。我是通过字典的形式保存,就可能出现某个字符在某一个状态没有频数,导致后面矩阵计算错误。为保证每个字符都在STATES的字典中,在构建发射概率矩阵是先初始化。
在中文分词初始状态概率指的是每一句话第一个字符的对应状态概率。在我实验中通过训练的得到的初始状态概率分布为,
{'B': -0.48164247830489765,'M': -3.14e+100, 'E': -3.14e+100, 'S': -0.96172723110752845}
可以看到第一个字符的初始状态只能是‘B’和‘S’。
这个时候我们就完成了训练阶段的参数估计,得到了三个概率矩阵,分别是:
TransProbMatrix: 转移概率矩阵(array_A)
EmitProbMatrix: 发射概率矩阵(array_B)
InitStatus: 初始状态分布(array_pi)
测试阶段Viterbi算法
在这里我们要做的是对测试数据进行分词,首先要做的就是对测试数据中每一个字符进行状态标注,这里使用的是Viterbi算法进行标注。
给一个测试语句‘小明是中国人’,首先标注第一个字‘小’,由于是第一个字,这里只需要用到初始状态概率矩阵和发射矩阵,
初始状态概率矩阵:
{'B': -0.48164247830489765,'M': -3.14e+100, 'E': -3.14e+100, 'S': -0.96172723110752845}
发射概率矩阵:
{‘B’:{‘小’:-6.04291273032},‘M’:{‘小’:-6.50192547556},‘E’:{‘小’:-7.88369576318},‘S’:{‘小’:-6.60403172082}}
然后标注概率矩阵tab为:
for state in STATES:
tab[0][state] = array_pi[state] + array_b[state]['小']这里我对矩阵取对数,所有只用‘+’即可,则得到第一个字‘小’的标注概率:
tab[0][‘B’]=-6.52455520862
tab [0][‘M’]=-3.14e+100
tab [0][‘E’]=-3.14e+100
tab [0][‘S’]=-7.56575895193
这里可以看到path[0][‘B’]> path[0][‘S’],则这句语句第一个字‘小’标注为‘B’
然后计算第二个字明,这时就需要状态转移概率矩阵array_A。这里有两个迭代过程,对于‘明’每一个状态state0都需要计算前一个字‘小’可能的每一个状态state1的概率prob,然后取max,
for state0 in STATES:
for state1 in STATES:
prob=tab[i-1][state1]+array_a[state1][state0]+array_b[state0][sentence[i]]这实际上就是一个动态规划最优路径的问题,对前一个字‘小’的每个状态state根据状态转移矩阵array_a和‘小’的标注概率tab,再加上这个字‘明’的发射概率array_b,得到‘明’这个字的标记概率
tab[1][‘B’]= -14.742836926340019
tab [1][‘M’]=-14.836146344717278
tab [1][‘E’]= -12.832943424756692
tab [1][‘S’]=-17.961024112859207
这里可以看到tab [1][‘E’]最大,这个就是‘明’这个字的标注为‘E’。然后对测试数据依次进行这个操作。
在测试阶段使用Viterbi标注时需要注意:若测试集中出现某一个字符,但这个字符在训练集中未出现,这个时候发射概率是没有的,这里需要做平滑处理,我这里采用的方式是:将所有未在训练集中出现的字符统一发射概率为发射概率矩阵的中位数。
在这里测试数据的标注已经得到,最后一步需要做的就是根据标注的状态进行分词。这里有几种情况:
(1)测试数据只有一个字符,直接输出
(2)测试数据标注的最后一个字符的状态不是‘S’和‘E’,这里需要进行修改
if tag[-1] == 'B' or tag[-1] == 'M': #最后一个字状态不是'S'或'E'则修改
if tag[-2] == 'B' or tag[-2] == 'M':
tag[-1] = 'S'
else:
tag[-1] = 'E'最后整个分词器就已经实现,这里需要对最后的分词结果进行测试,测试资源
这里写一下score脚本的使用方法,
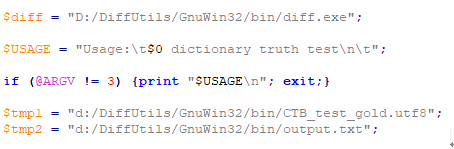
(1)这是一个perl的脚本,在windows系统中首先要下载一个ActivePerl的解释器,配置环境变量。
(2)然后score需要GNU diffutils的支持,下载地址
(3)然后需要修改score脚本中的语句,指定diff的安装目录$diff,$tmp1和$tmp2分别指定黄金标准分词文件和测试集切分文件。
我这里指定了tmp的路径,但是评分脚本“score”是用来比较两个分词文件的,需要三个参数:
1. 训练集词表(The training setword list)
2. “黄金”标准分词文件(The gold standard segmentation)
3. 测试集的切分文件(The segmentedtest file)
我在cmd中的命令输入为:
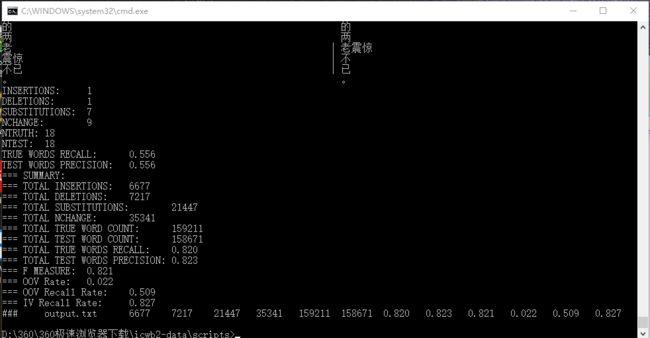
perl score CTB_training_words.utf8CTB_test_gold.utf8 output.txt
最后的分词结果为
实验代码:
GitHub链接:https://github.com/CQUPT-Wan/HMMwordseg.git
这个项目里面有我实现HMM中文分词的训练集,测试集和黄金标准分词文件
import pandas as pd
import codecs
from numpy import *
import numpy as np
import sys
import re
STATES = ['B', 'M', 'E', 'S']
array_A = {} #状态转移概率矩阵
array_B = {} #发射概率矩阵
array_E = {} #测试集存在的字符,但在训练集中不存在,发射概率矩阵
array_Pi = {} #初始状态分布
word_set = set() #训练数据集中所有字的集合
count_dic = {} #‘B,M,E,S’每个状态在训练集中出现的次数
line_num = 0 #训练集语句数量
#初始化所有概率矩阵
def Init_Array():
for state0 in STATES:
array_A[state0] = {}
for state1 in STATES:
array_A[state0][state1] = 0.0
for state in STATES:
array_Pi[state] = 0.0
array_B[state] = {}
array_E = {}
count_dic[state] = 0
#对训练集获取状态标签
def get_tag(word):
tag = []
if len(word) == 1:
tag = ['S']
elif len(word) == 2:
tag = ['B', 'E']
else:
num = len(word) - 2
tag.append('B')
tag.extend(['M'] * num)
tag.append('E')
return tag
#将参数估计的概率取对数,对概率0取无穷小-3.14e+100
def Prob_Array():
for key in array_Pi:
if array_Pi[key] == 0:
array_Pi[key] = -3.14e+100
else:
array_Pi[key] = log(array_Pi[key] / line_num)
for key0 in array_A:
for key1 in array_A[key0]:
if array_A[key0][key1] == 0.0:
array_A[key0][key1] = -3.14e+100
else:
array_A[key0][key1] = log(array_A[key0][key1] / count_dic[key0])
# print(array_A)
for key in array_B:
for word in array_B[key]:
if array_B[key][word] == 0.0:
array_B[key][word] = -3.14e+100
else:
array_B[key][word] = log(array_B[key][word] /count_dic[key])
#将字典转换成数组
def Dic_Array(array_b):
tmp = np.empty((4,len(array_b['B'])))
for i in range(4):
for j in range(len(array_b['B'])):
tmp[i][j] = array_b[STATES[i]][list(word_set)[j]]
return tmp
#判断一个字最大发射概率的状态
def dist_tag():
array_E['B']['begin'] = 0
array_E['M']['begin'] = -3.14e+100
array_E['E']['begin'] = -3.14e+100
array_E['S']['begin'] = -3.14e+100
array_E['B']['end'] = -3.14e+100
array_E['M']['end'] = -3.14e+100
array_E['E']['end'] = 0
array_E['S']['end'] = -3.14e+100
def dist_word(word0,word1,word2,array_b):
if dist_tag(word0,array_b) == 'S':
array_E['B'][word1] = 0
array_E['M'][word1] = -3.14e+100
array_E['E'][word1] = -3.14e+100
array_E['S'][word1] = -3.14e+100
return
#Viterbi算法求测试集最优状态序列
def Viterbi(sentence,array_pi,array_a,array_b):
tab = [{}] #动态规划表
path = {}
if sentence[0] not in array_b['B']:
for state in STATES:
if state == 'S':
array_b[state][sentence[0]] = 0
else:
array_b[state][sentence[0]] = -3.14e+100
for state in STATES:
tab[0][state] = array_pi[state] + array_b[state][sentence[0]]
# print(tab[0][state])
#tab[t][state]表示时刻t到达state状态的所有路径中,概率最大路径的概率值
path[state] = [state]
for i in range(1,len(sentence)):
tab.append({})
new_path = {}
# if sentence[i] not in array_b['B']:
# print(sentence[i-1],sentence[i])
for state in STATES:
if state == 'B':
array_b[state]['begin'] = 0
else:
array_b[state]['begin'] = -3.14e+100
for state in STATES:
if state == 'E':
array_b[state]['end'] = 0
else:
array_b[state]['end'] = -3.14e+100
for state0 in STATES:
items = []
# if sentence[i] not in word_set:
# array_b[state0][sentence[i]] = -3.14e+100
# if sentence[i] not in array_b[state0]:
# array_b[state0][sentence[i]] = -3.14e+100
# print(sentence[i] + state0)
# print(array_b[state0][sentence[i]])
for state1 in STATES:
# if tab[i-1][state1] == -3.14e+100:
# continue
# else:
if sentence[i] not in array_b[state0]: #所有在测试集出现但没有在训练集中出现的字符
if sentence[i-1] not in array_b[state0]:
prob = tab[i - 1][state1] + array_a[state1][state0] + array_b[state0]['end']
else:
prob = tab[i - 1][state1] + array_a[state1][state0] + array_b[state0]['begin']
# print(sentence[i])
# prob = tab[i-1][state1] + array_a[state1][state0] + array_b[state0]['other']
else:
prob = tab[i-1][state1] + array_a[state1][state0] + array_b[state0][sentence[i]] #计算每个字符对应STATES的概率
# print(prob)
items.append((prob,state1))
# print(sentence[i] + state0)
# print(array_b[state0][sentence[i]])
# print(sentence[i])
# print(items)
best = max(items) #bset:(prob,state)
# print(best)
tab[i][state0] = best[0]
# print(tab[i][state0])
new_path[state0] = path[best[1]] + [state0]
path = new_path
prob, state = max([(tab[len(sentence) - 1][state], state) for state in STATES])
return path[state]
#根据状态序列进行分词
def tag_seg(sentence,tag):
word_list = []
start = -1
started = False
if len(tag) != len(sentence):
return None
if len(tag) == 1:
word_list.append(sentence[0]) #语句只有一个字,直接输出
else:
if tag[-1] == 'B' or tag[-1] == 'M': #最后一个字状态不是'S'或'E'则修改
if tag[-2] == 'B' or tag[-2] == 'M':
tag[-1] = 'E'
else:
tag[-1] = 'S'
for i in range(len(tag)):
if tag[i] == 'S':
if started:
started = False
word_list.append(sentence[start:i])
word_list.append(sentence[i])
elif tag[i] == 'B':
if started:
word_list.append(sentence[start:i])
start = i
started = True
elif tag[i] == 'E':
started = False
word = sentence[start:i + 1]
word_list.append(word)
elif tag[i] == 'M':
continue
return word_list
if __name__ == '__main__':
trainset = open('CTBtrainingset.txt', encoding='utf-8') #读取训练集
testset = open('CTBtestingset.txt', encoding='utf-8') #读取测试集
# trainlist = []
Init_Array()
for line in trainset:
line = line.strip()
# trainlist.append(line)
line_num += 1
word_list = []
for k in range(len(line)):
if line[k] == ' ':continue
word_list.append(line[k])
# print(word_list)
word_set = word_set | set(word_list) #训练集所有字的集合
line = line.split(' ')
# print(line)
line_state = [] #这句话的状态序列
for i in line:
line_state.extend(get_tag(i))
# print(line_state)
array_Pi[line_state[0]] += 1 # array_Pi用于计算初始状态分布概率
for j in range(len(line_state)-1):
# count_dic[line_state[j]] += 1 #记录每一个状态的出现次数
array_A[line_state[j]][line_state[j+1]] += 1 #array_A计算状态转移概率
for p in range(len(line_state)):
count_dic[line_state[p]] += 1 # 记录每一个状态的出现次数
for state in STATES:
if word_list[p] not in array_B[state]:
array_B[state][word_list[p]] = 0.0 #保证每个字都在STATES的字典中
# if word_list[p] not in array_B[line_state[p]]:
# # print(word_list[p])
# array_B[line_state[p]][word_list[p]] = 0
# else:
array_B[line_state[p]][word_list[p]] += 1 # array_B用于计算发射概率
Prob_Array() #对概率取对数保证精度
print('参数估计结果')
print('初始状态分布')
print(array_Pi)
print('状态转移矩阵')
print(array_A)
print('发射矩阵')
print(array_B)
output = ''
for line in testset:
line = line.strip()
tag = Viterbi(line, array_Pi, array_A, array_B)
# print(tag)
seg = tag_seg(line, tag)
# print(seg)
list = ''
for i in range(len(seg)):
list = list + seg[i] + ' '
# print(list)
output = output + list + '\n'
print(output)
outputfile = open('output.txt', mode='w', encoding='utf-8')
outputfile.write(output)参考链接:
http://www.leexiang.com/hidden-markov-model
http://www.52nlp.cn/category/hidden-markov-model
最后如果转载,麻烦留个本文的链接,因为如果读者或我自己发现文章有错误,我会在这里更正,留个本文的链接,防止我暂时的疏漏耽误了他人宝贵的时间。