实习和秋招计算机视觉cv岗面试总结
实习和秋招计算机视觉cv岗面试总结
欢迎来到一个小菜鸡的总结
有点兴奋,第一次写博客2333。
今年情况
先写点啥呢,感觉算法岗啊,血淋淋的呀:
- 死伤无数 ,有可以拿bat,字节的,但大多并没有;
- 文章,大厂实习,想拿大厂算法offer的大多有这俩条件之一;
- 今年算法hc减少,明年不知道啥情况;
面试包装
拿offer条件:数据结构刷题 + 数学+拿得出手的项目
开始吧!!!
Yolo 和Fast RCNN
比较流行的算法可以分为两类,一类是基于Region Proposal的R-CNN系算法(R-CNN,Fast R-CNN, Faster R-CNN),它们是two-stage的,需要先使用启发式方法(selective search)或者CNN网络(RPN)产生Region Proposal,然后再在Region Proposal上做分类与回归。而另一类是Yolo,SSD这类one-stage算法,其仅仅使用一个CNN网络直接预测不同目标的类别与位置。第一类方法是准确度高一些,但是速度慢,但是第二类算法是速度快,但是准确性要低一些。
详情链接:link
使用TensorFlow训练模型时,突然报错出现OMP线程过多的问题
OMP线程过多的问题:link
解决之后又出现显存耗尽问题:link
清理无进程显存:link
keras限制用量:link
批量终止进程:link
Python的多线程能否用来做并行计算?
不能,它有GIL锁,但可以用多进程实现并行:link
SIFT特征是如何保持旋转不变性的?
sift特征通过将坐标轴旋转至关键点的主方向来保持旋转不变性,关键点的主方向是通过统计关键点局部邻域内像素梯度的方向分布直方图的最大值得到的。(变量越少,观察结果变化的可能性就越小)
详情链接:link
影响神经网络速度的4个因素
- FLOPs(FLOPs就是网络执行了多少multiply-adds操作);
- MAC(内存访问成本);
- 并行度(如果网络并行度高,速度明显提升);
- 计算平台(GPU,ARM)
L1正则化和L2正则化的区别
L1正则化和L2正则化可以看做是损失函数的惩罚项。
对于线性回归模型,使用L1正则化的模型建叫做Lasso回归,使用L2正则化的模型叫做Ridge回归(岭回归)
相同点:都用于避免过拟合
不同点:L1可以让一部分特征的系数缩小到0,从而间接实现特征选择。所以L1适用于特征之间有关联的情况。
L2让所有特征的系数都缩小,但是不会减为0,它会使优化求解稳定快速。所以L2适用于特征之间没有关联的情况
详情链接:link
Tensorflow中训练得到Nan错误的分析
详情链接:link
C++中,引用和指针的区别是什么?
1、引用在创建时必须初始化,引用到一个有效对象;而指针在定义时不必初始化,可以在定义后的任何地方重新赋值。
2、指针可以是NULL,引用不行
3、引用貌似一个对象的小名,一旦初始化指向一个对象,就不能将其他对象重新赋值给该引用,这样引用和原对象的值都会被更改。
4、引用的创建和销毁不会调用类的拷贝构造函数和析构函数。
Android NDK是什么意思?
Android 应用是在dalvik虚拟机中运行的。NDK可以让你使用本地代码语言来开发应用,比如说C/C++,这种方法对某些类型的应用的是有好处的,可以充分利用本地代码和在某些情况下加速代码的执行。
NDK提供了一系列的工具,帮助开发者快速开发C(或C++)的动态库,并能自动将so和java应用一起打包成apk。
NDK集成了交叉编译器,并提供了相应的mk文件隔离CPU、平台、ABI等差异,开发人员只需要简单修改mk文件(指出”哪些文件需要编译”、”编译特性要求”等),就可以创建出so。
NDK可以自动地将so和Java应用一起打包,极大地减轻了开发人员的打包工作。
BN层
输入:输入数据x1…xm(这些数据是准备进入激活函数的数据)
计算过程中可以看到,
1.求数据均值
2.求数据方差
3.数据进行标准化(个人认为称作正态化也可以)
4.训练参数γ,β
5.输出y通过γ与β的线性变换得到新的值
在正向传播的时候,通过可学习的γ与β参数求出新的分布值
在反向传播的时候,通过链式求导方式,求出γ与β以及相关权值
Tensorflow的原理,技术细节
详情:link
简述Canny算法,还有什么边缘检测算法,各自的优缺点
边缘提取其实也是一种滤波,不同的算子有不同的提取效果。比较常用的方法有三种,Sobel算子,Laplacian算子,Canny算子。
Sobel算子检测方法对灰度渐变和噪声较多的图像处理效果较好,sobel算子对边缘定位不是很准确,图像的边缘不止一个像素;当对精度要求不是很高时,是一种较为常用的边缘检测方法。
Canny方法不容易受噪声干扰,能够检测到真正的弱边缘。优点在于,使用两种不同的阈值分别检测强边缘和弱边缘,并且当弱边缘和强边缘相连时,才将弱边缘包含在输出图像中。
Laplacian算子法对噪声比较敏感,所以很少用该算子检测边缘,而是用来判断边缘像素视为与图像的明区还是暗区。拉普拉斯高斯算子是一种二阶导数算子,将在边缘处产生一个陡峭的零交叉, Laplacian算子是各向同性的,能对任何走向的界线和线条进行锐化,无方向性。这是拉普拉斯算子区别于其他算法的最大优点。
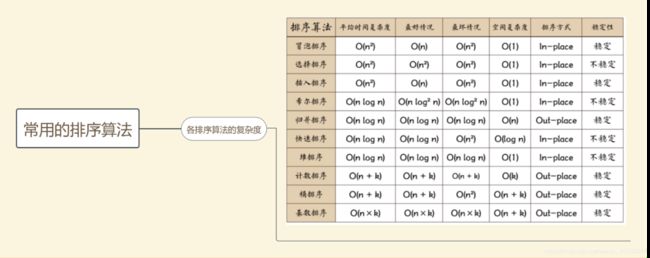
排序算法了解哪些,介绍一下快速排序,以及他们的时间复杂度情况
• stable sort:插入排序、冒泡排序、归并排序、计数排序、基数排序、桶排序。
• unstable sort:选择排序、快速排序、堆排序。
快排的基本思想是:
在序列中找一个划分值,通过一趟排序将未排序的序列排序成 独立的两个部分,其中左边部分序列都比划分值小,右边部分的序列比划分值大,此时划分值的位置已确认,然后再对这两个序列按照同样的方法进行排序,从而达到整个序列都有序的目的。
为什么使用交叉熵作为损失函数
模型压缩的大方向。CPM 模型怎么压缩的?
对于模型压缩这一块的方法大致可以分为:低秩近似(low-rank Approximation),网络剪枝(network pruning),网络量化(network quantization),知识蒸馏(knowledge distillation)和紧凑网络设计(compact Network design)
频率学派和贝叶斯学派的区别?
认为世界无时无刻不在改变,未知的变量和事件都有一定的概率,即后验概率是先验概率的修正。频率派认为模型参数是固定的,一个模型在无数次抽样后,参数是不变的。而贝叶斯学派认为数据才是固定的而参数并不是。频率派认为模型不存在先验而贝叶斯派认为模型存在先验。
训练时候loss降不下来怎么办?
train loss 不断下降,test loss不断下降,说明网络仍在学习;
train loss 不断下降,test loss趋于不变,说明网络过拟合;
train loss 趋于不变,test loss不断下降,说明数据集100%有问题;
train loss 趋于不变,test loss趋于不变,说明学习遇到瓶颈,需要减小学习率或批量数目;
train loss 不断上升,test loss不断上升,说明网络结构设计不当,训练超参数设置不当,数据集经过清洗等问题。
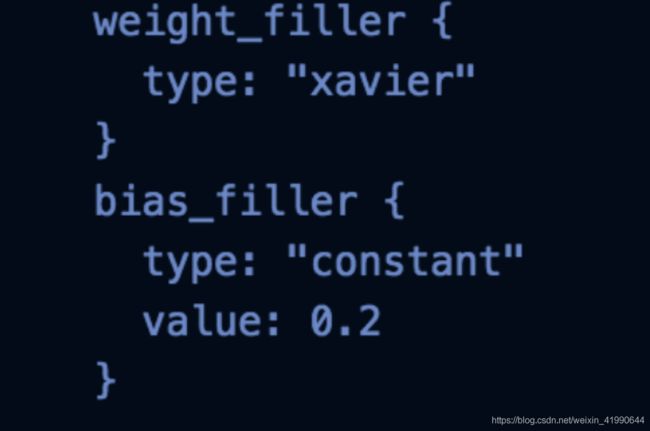
参数初始化
如何提高python的运行效率?
1、使用生成器,因为可以节约大量内存
2、循环代码优化,避免过多重复代码的执行
3、核心模块用Cython PyPy等,提高效率
4、多进程、多线程、协程
5、多个if elif条件判断,可以把最有可能先发生的条件放到前面写,这样可以减少程序判断的次数,提高效率
逻辑回归解释一下,极大似然估计呢
逻辑回归(Logistic Regression)是一种用于解决二分类(0 or 1)问题的机 器学习方法,用于估计某种事物的可能性。
逻辑回归与线性回归都是一种广义线性模型。逻辑回归假设因变量 y 服从伯努利分布,而线性回归假设因变量 y 服从高斯分布。 因此与线性回归有很多相同之处,去除Sigmoid映射函数的话,逻辑回归算法就是一个线性回归。可以说,逻辑回归是以线性回归为理论支持的,但是逻辑回归通过Sigmoid函数引入了非线性因素,因此可以轻松处理0/1分类问题。
生成模型和判别模型的区别?
生成模型是先从数据中学习联合概率分布,然后利用贝叶斯公式求得特征和标签对应的条件概率分布。判别模型直接学习条件概率分布,直观的输入什么特征就预测可能的类别。
生成式模型(Generative Model)则会对x和y的联合分布p(x,y)建模,然后通过贝叶斯公式来求得p(yi|x),然后选取使得p(yi|x)最大的yi
常见的生成式模型有隐马尔可夫模型HMM、朴素贝叶斯模型、高斯混合模型GMM、狄利克雷分布模型(Latent Dirichlet Allocation,LDA)等
判别式模型(Discriminative Model)是直接对条件概率p(y|x;θ)建模。
常见的判别式模型有线性回归模型、线性判别分析、支持向量机SVM、神经网络等。
bagging和boosting的区别
Baggging 和Boosting都是模型融合的方法,可以将弱分类器融合之后形成一个强分类器,而且融合之后的效果会比最好的弱分类器更好。
Bagging和Boosting的区别:
1)样本选择上:
Bagging:训练集是在原始集中有放回选取的,从原始集中选出的各轮训练集之间是独立的。
Boosting:每一轮的训练集不变,只是训练集中每个样例在分类器中的权重发生变化。而权值是根据上一轮的分类结果进行调整。
2)样例权重:
Bagging:使用均匀取样,每个样例的权重相等
Boosting:根据错误率不断调整样例的权值,错误率越大则权重越大。
3)预测函数:
Bagging:所有预测函数的权重相等。
Boosting:每个弱分类器都有相应的权重,对于分类误差小的分类器会有更大的权重。
4)并行计算:
Bagging:各个预测函数可以并行生成
Boosting:各个预测函数只能顺序生成,因为后一个模型参数需要前一轮模型的结果。
堆排序
def big_endian(arr, start, end):
root = start
child = root * 2 + 1 # 左孩子
while child <= end:
# 孩子比最后一个节点还大,也就意味着最后一个叶子节点了,就得跳出去一次循环,已经调整完毕
if child + 1 <= end and arr[child] < arr[child + 1]:
# 为了始终让其跟子元素的较大值比较,如果右边大就左换右,左边大的话就默认
child += 1
if arr[root] < arr[child]:
# 父节点小于子节点直接交换位置,同时坐标也得换,这样下次循环可以准确判断:是否为最底层,
# 是不是调整完毕
arr[root], arr[child] = arr[child], arr[root]
root = child
child = root * 2 + 1
else:
break
def heap_sort(arr): # 无序区大根堆排序
first = len(arr) // 2 - 1
for start in range(first, -1, -1):
# 从下到上,从左到右对每个节点进行调整,循环得到非叶子节点
big_endian(arr, start, len(arr) - 1) # 去调整所有的节点
for end in range(len(arr) - 1, 0, -1):
arr[0], arr[end] = arr[end], arr[0] # 顶部尾部互换位置
big_endian(arr, 0, end - 1) # 重新调整子节点的顺序,从顶开始调整
return arr
def main():
l = [3, 1, 4, 9, 6, 7, 5, 8, 2, 10]
print(heap_sort(l))
if __name__ == "__main__":
main()
写完来波音乐安利(有点皮)
| 歌名 | 原因 |
|---|---|
| 异乡人 | 昏黄路灯下,独自走在异乡街上,嗯,别的不说了 |
| Let’s not fall in love | 最喜欢的Big Bang 的歌曲,没有之一,推荐看他们演唱会MV |
| 生生 | 有时会很符合心情,哈哈哈 |
| Apologize | 原因很简单,洗脑 |
| The Fox | 有点搞笑的一首歌 |
不喜欢数学却很喜欢的一个数学公式(在装x)
e i π + 1 = 0 e^{i\pi}+1=0 eiπ+1=0

