OpenCV4学习笔记（34）——Farneback稠密光流算法

在上次的博文OpenCV4学习笔记（33）——KLT稀疏光流跟踪算法中，整理记录的OpenCV中对于KLT稀疏光流跟踪的实现，同时也提到了光流跟踪算法除了稀疏光流跟踪以外，还有稠密光流跟踪算法。所以今天要整理的笔记内容就是在OpenCV中对于稠密光流跟踪算法的实现。

先来回顾一下KLT稀疏光流跟踪算法，它是基于shi-tomas角点检测来实现的，只需要每个特征角点的邻域空间窗口内的局部信息来实现光流跟踪。这种基于局部点的光流跟踪方法带来的优点是运行速度快，但是缺点则是跟踪效果较为一般。

而Farneback稠密光流算法则是基于前后两帧图像中所有像素点的移动估算算法，通过前后两帧图像中所有像素点的位移矢量来实现光流跟踪。由于Fb稠密光流算法需要检测所有像素点的光流，所以其效果比稀疏光流算法要更好，但是相对而言其速度更慢，如果没有经过特殊优化的化是不适合用于实时处理的。

Farneback稠密光流算法的主要实现思路是通过每个像素点的邻域信息（由邻域像素点的像素值大小和位置来确定权重）来对该像素点的坐标位置进行多项式展开，得到一个以原坐标（x0，y0）为自变量，新坐标（x，y）为因变量的多项式，并代入坐标数据来求取该像素点在x和y方向上的移动量（dx，dy）。这样就得到了每个像素点在前后两帧图像中的位移矢量，包含振幅和相位。

如果我们将每个像素点位移矢量的振幅和相位信息转化为H、S、V三通道信息，就可以在视频流中直观地观察运动物体的运动情况了，也就实现了对于运动物体的稠密光流跟踪。

在OpenCV中提供了calcOpticalFlowFarneback（）这个API来进行稠密光流的计算，这个API使用的是图像金字塔的FB稠密光流算法，它是对上一帧和当前帧图像分别建立图像金字塔，再分别对两个图像金字塔自顶向底地对同一层图像进行FB算法的计算。由于在低分辨率层图像中，运动速度较快的物体不易逃脱检测窗口的捕捉，有利于检测运动程度较大的目标，所以使用图像金字塔的FB稠密光流算法相比一般的FB稠密光流算法具有更好的鲁棒性，能够允许目标比较大程度的运动。

calcOpticalFlowFarneback（）的参数含义如下：

第一个参数prev：输入的上一帧图像，为8位单通道图；

第二个参数next：输入的当前帧（或者叫下一帧）图像，为8位单通道图；

第三个参数flow：输出的光流矩阵，其尺寸和输入图像一致，矩阵中每个元素都是一个Point2f类型的点，表示在输入图像中相同位置的像素点在上一帧和当前帧图像中分别在x方向和y方向的位移，即（dx，dy）；

第四个参数pyr_scale：生成图像金字塔时上下两层的缩放比例，取值范围是0~1；当该参数为0.5时，即为经典的图像金字塔；

第五个参数level：生成的图像金字塔的层数；当level=0时表示不使用图像金字塔的FB稠密光流算法；一般取level=3；

第六个参数winsize：表示滤波和检测的窗口大小，该参数越大对噪声抑制能力越强，并且能够检测快速移动目标（目标像素点不会移出窗口），但会引起运动区域的模糊；

第七个参数iterations：对每层金字塔图像进行FB算法时的迭代次数；

第八个参数poly_n：对当前像素点进行多项式展开时所选用的邻域大小，该参数值越大，运动区域模糊程度越大，对目标运动检测更稳定，会产生更鲁棒的算法和更模糊的运动场，官方推荐poly_n = 5或7；

第九个参数poly_sigma：进行多项式展开时的高斯系数；推荐值为：当poly_n = 5时，poly_sigma = 1.1；当poly_n = 7时，poly_sigma = 1.5；

第十个参数flag：进行光流估算的滤波器，有以下两种选择：
（1）OPTFLOW_USE_INITIAL_FLOW使用输入流作为初始流近似值，并使用盒子滤波器进行光流估算；
（2）OPTFLOW_FARNEBACK_GAUSSIAN使用高斯滤波器进行光流估算，高斯滤波器相比盒子滤波器的估算结果更精确，但运行速度较慢。

下面是具体的代码演示：

	VideoCapture capture;
	//capture.open("D:\\opencv_c++\\opencv_tutorial\\data\\images\\video.avi");
	capture.open("D:\\OpenCV\\opencv\\sources\\samples\\data\\vtest.avi");
	if (!capture.isOpened())
	{
		return 0;
	}
	Mat pre_gray, now_gray;
	capture.read(pre_gray);
	cvtColor(pre_gray, pre_gray, COLOR_BGR2GRAY);
	Mat flow = Mat::zeros(pre_gray.size(), CV_32FC2);

	Mat frame, move_x, move_y;
	move_x = Mat::zeros(flow.size(), CV_32F);
	move_y = Mat::zeros(flow.size(), CV_32F);
	while (capture.read(frame))
	{
		cvtColor(frame, now_gray, COLOR_BGR2GRAY);
		calcOpticalFlowFarneback(pre_gray, now_gray, flow, 0.5, 3, 9, 1, 7, 1.5, OPTFLOW_FARNEBACK_GAUSSIAN);
		for (int row = 0; row < flow.rows; row++)
		{
			for (int col = 0; col < flow.cols; col++)
			{
				//遍历光流矩阵，将x和y方向上的移动值分别存放为独立的矩阵
				Point2f move_x_y = flow.at<Point2f>(row, col);
				move_x.at<float>(row, col) = move_x_y.x;
				move_y.at<float>(row, col) = move_x_y.y;
			}
		}

		Mat mag, ang;
		cartToPolar(move_x, move_y, mag, ang);		//将移动矢量从笛卡尔坐标转换极坐标，输出像素点移动的幅度和相位（弧度）
		Mat H, S, V;
		//以相位值来确定色调H，像素点的不同移动方向形成不同颜色
		H = ang * 180 / CV_PI / 2;			//将弧度转为角度，且在OpenCV中H取值范围是0~180°
		convertScaleAbs(H, H);
		//饱和度S设置最大255，色彩最浓，有利于观察
		S = Mat::zeros(move_x.size(), CV_8UC1);
		S = Scalar(255);
		//亮度V由像素点的移动幅度决定，幅度越大则亮度越大
		normalize(mag, V, 0, 255, NORM_MINMAX);
		convertScaleAbs(V, V);

		vector<Mat> HSV(3);
		HSV[0] = H;
		HSV[1] = S;
		HSV[2] = V;
		Mat result;
		merge(HSV, result);
		//转换到RGB色彩空间进行显示
		cvtColor(result, result, COLOR_HSV2BGR);
		imshow("result", result);

		char ch = cv::waitKey(20);
		if (ch == 27)
		{
			break;
		}
		//将当前帧图像，置为上一帧图像
		swap(pre_gray, now_gray);

	}
	capture.release();

当调用calcOpticalFlowFarneback（）后，我们得到一个包含x、y两个方向移动量的矩阵，于是我们通过双重for循环来遍历光流矩阵，将x和y方向上的移动量分别存放到两个独立的矩阵中去。这两个矩阵相当于位移矢量在x、y方向的分量，组合起来就表示每个像素点在前后两帧图像中移动的位移矢量。

接着，再通过cartToPolar（）这个API，将上述得到的两个位移矢量分量从笛卡尔坐标系变换到极坐标系中，从而得到位移矢量的振幅和相位。
cartToPolar（）这个API的参数如下：
第一个参数x：输入的x分量数据，也就是dx；
第二个参数y：输入的y分量数据，也就是dy；
第三个参数magnitude：输出的振幅信息；
第四个参数angle：输出的相位信息。

随后我们将振幅和相位信息转化到HSV空间中。由于相位和色调的取值范围都是 0~2Π ，所以可以利用相位信息来计算出色调H的值，计算公式为H = ang * 180 / CV_PI / 2，将相位由弧度转为角度，且在OpenCV中色调H取值范围是0~180°，所以再除以2。这样通过不同方向的位移计算得到的色调H是不一样的，就给不同移动方向的像素点分配了不同显示色彩，便于观察。

对于饱和度S，我们统一设置为最大值255，用最浓的色彩来显示同样便于我们观察。

最后通过振幅来计算亮度V，也就是将振幅归一化到0~255之间，如果振幅越大则亮度V越大，也就是目标物体的运动程度越大，则显示得更亮。

最后将得到的HSV图像转化为RGB图像，就能够直观得显示出对运动物体的光流跟踪效果了。

下面是演示效果的截图：


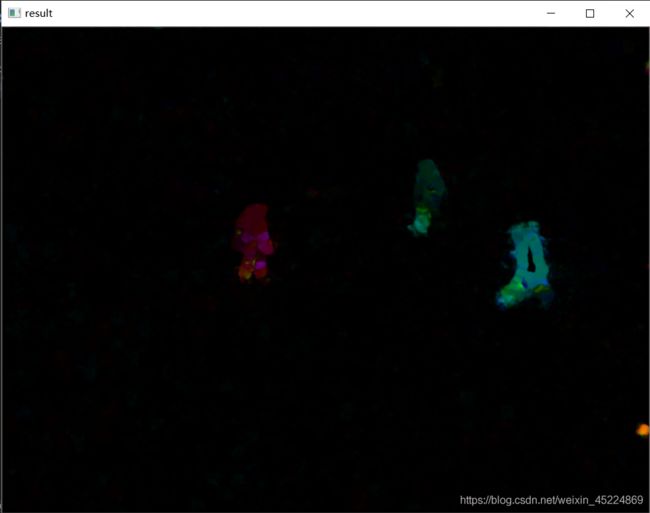
从效果图中可以看出，Farneback稠密光流跟踪算法能够将视频中走动的人检测出来，而且不同方向和不同运动程度都能够直观地显示出来，这样我们就可以实现基于Farneback稠密光流算法的运动检测。然而，这种方式实现运动检测的实时性很差，在视频播放过程可以看出非常明显的卡顿现象，可能在运算速度上的缺陷也一定程度上限制了Farneback算法的应用吧。

好的，今天的笔记就记录到这里，下次有空再来写博客啦~

PS：本人的注释比较杂，既有自己的心得体会也有网上查阅资料时摘抄下的知识内容，所以如有雷同，纯属我向前辈学习的致敬，如果有前辈觉得我的笔记内容侵犯了您的知识产权，请和我联系，我会将涉及到的博文内容删除，谢谢！