前言
oh 肉丝
oh 杰克
you jump! i jump!
yeah 一起沉浸在jump的喜悦里
今天跟大家来聊聊redis的跳跃表
everybody 都需要了解的跳跃表 不仅仅是概念 还有代码 强烈建议阅读《Redis5 设计与源码分析》陈雷编著
有序集合
我们先看看我们平时常用的关于redis的有序集合
大家常用的命令如下
127.0.0.1:6379> zadd jump 1 jack
(integer) 1
127.0.0.1:6379> zadd jump 2 rose
(integer) 1
127.0.0.1:6379> zrange jump 0 1
1) "jack"
2) "rose"redis的有序集合的复杂度ZADD O(M*log(N)), N 是有序集的基数, M 为成功添加的新成员的数量。ZRANGE O(log(N)+M), N 为有序集的基数,而 M 为结果集的基数ZRANK O(log(N))ZSCORE O(1)
我们不妨可以思考下,什么样的数据结构能满足上述,来这时候拿出我们的数据结构知识储备了。线性表、链表、栈与队列、串、树它全家系列想想哪种能符合上述
也是常见问题 为什么使用跳表当数据结构
- 线性表 查找符合 添加和删除 是O(n) 不可以
- 链表 添加和删除符合 查找是O(n) 不可以
- 树 (不管是什么二叉、红黑、B它全家)好像复杂度可以满足 但是我们看看
zscore是O(1) 好像不是内味
而且树的实现有多蛋疼,可以经常听到以下对话
你可以手撕 ** 树吗
我可以爬 ** 树 你看可以吗?
zscore 返回有序集 key 中,成员 member 的 score 值。如果是O(1)的话 有链表那味
那么我猜跳表就是链表的它私生子,绝对不是树的私生子。
跳跃表
事实上,跳表是一个多层的有序双向链表
有一座楼,有三层高,每个人都会影子分身术,可以每层楼放自己影子(放不放看每个人的心情,一旦定了就不能后悔),并且每个房间都有通往下一层的楼梯。这里有3个人分别狗蛋A、狗蛋B、狗蛋C,有一次考试结束
狗蛋A 考了60分
狗蛋B 考了80分
狗蛋C 考了100分
每个狗蛋根据分数自己排了顺序,考的好的站后面。
狗蛋他爸住在最顶楼(第二层) 想问问谁考了100分
大概图长这个样子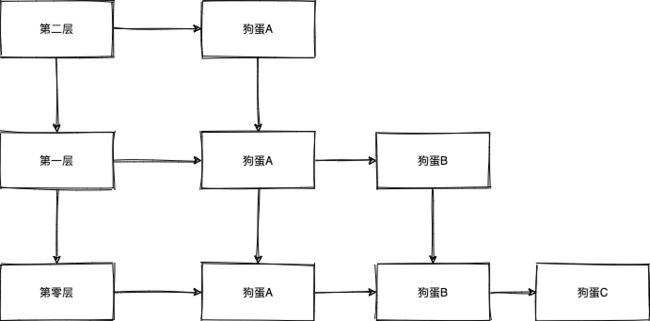
1.狗蛋他爸问狗蛋A:你多少分。 狗蛋A说:60,这层后面没狗蛋了。
2.狗蛋他爸在狗蛋A的房间往下一层走。
4.看到了狗蛋B:狗蛋B说80分,后面没有狗蛋了。
5.狗蛋他爸在狗蛋B的房间往下走,发现了狗蛋C,并且就是考了100的那的狗蛋。
路线大概是这样子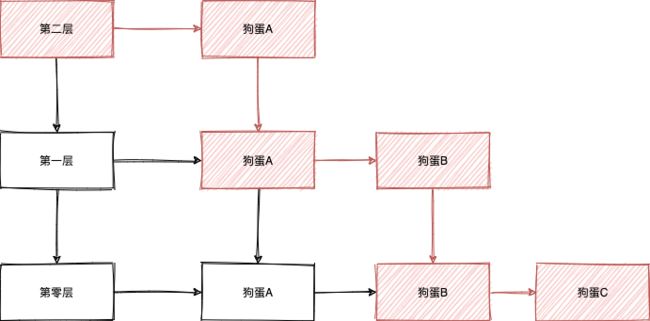
看了源码你会发现每个狗蛋几层高真的是看狗蛋心情。
分析源码
有人说:跳跃表概念我也懂,有本事直接撸源码。
撸就撸,来,大家一起撸 ~~~~~~~ 源码
结构体
/**
* 跳跃表节点的结构体
*/
typedef struct zskiplistNode {
// 用动态字符串的数据key(member)的类型 如果头节点 NULL
sds ele;
// 对应的排序分值 如果头节点 NULL
double score;
// 指向前一个节点的戒指 当然头节点指向的NULL
struct zskiplistNode *backward;
// 柔性数组 数组大小 参照zslRandomLevel(void) 长度为1到 64
struct zskiplistLevel {
// 指向前一个节点的戒指 当然头节点指向的NULL
struct zskiplistNode *forward;
// 表示该层下的节点数量
unsigned long span;
} level[];
} zskiplistNode;
/**
* 跳跃表结构体
*/
typedef struct zskiplist {
// 指向跳跃表的头和尾部
struct zskiplistNode *header, *tail;
// 跳跃表长度 除去头节点
unsigned long length;
// 跳跃表的层级
int level;
} zskiplist;
根据上述的狗蛋图和跳跃表的结构体,看看能不能在心中有个实现思路。如果有的话,就不要往下看了,我怕看了你被我带偏。
跳跃表的基本知识点
1.层高最多64层,具体层高看心情(随机生成,越大越概率越低)
2.每层都是有序双向链表(有前进指针和后退指针)
3.header节点就是类似大学的宿管(知道每层的房间数和当层下一个房间的指针)
4.每一层最后的一个节点都是指向NULL(就是用下个节点是为NULL判断是不是本层最后一个)
5.第0层也就是最后一层的节点上数量就是跳跃表的实际长度(想想上述例子,地基都打在第一层,当然能知道整个具体长度)
源码分析
zslRandomLevel
#define ZSKIPLIST_MAXLEVEL 64 /* Should be enough for 2^64 elements */
#define ZSKIPLIST_P 0.25 /* Skiplist P = 1/4 */
/**
* 随机生产跳跃表节点的层高
* @return
*/
int zslRandomLevel(void) {
// 默认层高 1层
int level = 1;
// &0xFFFF = 65535 只取低16位 相当于只获取 1 ~ 65535
// ZSKIPLIST_P -> 0.25
while ((random()&0xFFFF) < (ZSKIPLIST_P * 0xFFFF))
level += 1;
// 最终的概率为 1/(1 - ZSKIPLIST_P)
return (level你看吧每个狗蛋的层高的真的看心情。
zslCreate
/**
* 初始化跳跃表
* @return
*/
zskiplist *zslCreate(void) {
int j;
zskiplist *zsl;
// 初始化跳跃表内存
zsl = zmalloc(sizeof(*zsl));
// 默认一层
zsl->level = 1;
// 长度默认0
zsl->length = 0;
// 初始化默认头节点
zsl->header = zslCreateNode(ZSKIPLIST_MAXLEVEL,0,NULL);
// 默认跳跃表为64层
for (j = 0; j < ZSKIPLIST_MAXLEVEL; j++) {
zsl->header->level[j].forward = NULL;
zsl->header->level[j].span = 0;
}
// 后退指针
zsl->header->backward = NULL;
// 尾指针
zsl->tail = NULL;
return zsl;
}zslInsert
/** 插入跳跃表节点
*
* @param zsl 管理跳跃表
* @param score 分值
* @param ele 字符串
* @return
*/
zskiplistNode *zslInsert(zskiplist *zsl, double score, sds ele) {
zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
unsigned int rank[ZSKIPLIST_MAXLEVEL];
int i, level;
serverAssert(!isnan(score));
x = zsl->header;
for (i = zsl->level-1; i >= 0; i--) {
rank[i] = i == (zsl->level-1) ? 0 : rank[i+1];
// 有下节点 且 下个节点小于当前的分值 且 (如果节点分值相同的情况下 比较key的字典)
while (x->level[i].forward &&
(x->level[i].forward->score < score ||
(x->level[i].forward->score == score &&
sdscmp(x->level[i].forward->ele,ele) < 0)))
{
// 保存每个层的步长
rank[i] += x->level[i].span;
x = x->level[i].forward;
}
// 记录每个前节点
update[i] = x;
}
// update[i] 记录每个层的前节点
// rank[i] 记录每个层的需要更新的步长
// 初始化需要插入节点的层高
level = zslRandomLevel();
// 如果插入的节点层高 大于 跳跃表的层高
if (level > zsl->level) {
// 需要将多出的层高
for (i = zsl->level; i < level; i++) {
rank[i] = 0;
update[i] = zsl->header;
update[i]->level[i].span = zsl->length;
}
zsl->level = level;
}
// 创建需要插入跳跃表的节点
x = zslCreateNode(level,score,ele);
for (i = 0; i < level; i++) {
// 每一层为有序链表 参照插入链表的做法
x->level[i].forward = update[i]->level[i].forward;
update[i]->level[i].forward = x;
x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);
// 更新步长
update[i]->level[i].span = (rank[0] - rank[i]) + 1;
}
// 因为插入一个节点 需要每层的span都需要+1
for (i = level; i < zsl->level; i++) {
update[i]->level[i].span++;
}
// 每个节点的 后退指针都指向 第一层的 前一个节点 如果插入的节点不是头节点
x->backward = (update[0] == zsl->header) ? NULL : update[0];
// 如果插入的节点后面有节点
if (x->level[0].forward)
// 则后面节点的后退指针指向自己
x->level[0].forward->backward = x;
else
// 如果没有节点 则 插入的节点为最后一个节点 尾指针指向自己
zsl->tail = x;
// 增加跳跃表的长度 因为插入一个节点
zsl->length++;
return x;
}现在看不懂具体代码实现没关系,因为本篇文章没打算让你看懂具体实现,具体代码可以自己下载redis 5.0版本里t_zset.c文件或者可以购买《Redis5 设计与源码分析》陈雷编著 (强烈推荐后者)。
最后
如果你以后成为面试官,问别人有序集合的底层实现是什么?
如果那个人说是跳跃表。
请你杠回去,有序集合底层实现使用跳跃表和压缩列表根据参数配置zset-max-ziplust-entris和zset-max-ziplist-value决定
/* Lookup the key and create the sorted set if does not exist. */
zobj = lookupKeyWrite(c->db,key);
if (zobj == NULL) {
if (xx) goto reply_to_client; /* No key + XX option: nothing to do. */
if (server.zset_max_ziplist_entries == 0 ||
server.zset_max_ziplist_value < sdslen(c->argv[scoreidx+1]->ptr))
{
zobj = createZsetObject();
} else {
zobj = createZsetZiplistObject();
}
dbAdd(c->db,key,zobj);
}文章如果有描述错误的地方,恳请留言矫正。


