【深度学习】第一篇：深度学习与 TensorFlow 基础

 
　　　　　　　　转载说明出处：https://blog.csdn.net/qq_41709378/article/details/107942274
　　　　　　　　　　　　　
博客内容是书籍： 《深度学习之TensorFlow入门、原理与进阶实战》 的阅读笔记。
　　　　　　　　　　　　　　　　　　　
博客内容是书籍中 第一篇：深度学习与 TensorFlow 基础 的部分。
内容分为三个部分：
　　　　第一部分：遇到的问题总结
　　　　第二部分：第三章 ：TensorFlow 基本开发步骤 - 以逻辑回归拟合二维数据为例
　　　　第三部分：第五章 ：识别图中模糊的手写数字
　　　　
 
 
课件 PDF 和 源码 移步到Github ： https://github.com/Stormzudi/Python-Data-Mining
Tensorflow 2.0官网 ：https://tensorflow.google.cn/versions/r2.0/api_docs/python/tf
邮箱：[email protected]

---

简单说下：第一章、第二章、第四章的内容在原书籍中讲解的非常详细，如遇到安装问题可以直接在网上搜索解决方案。
运行环境：Tensorflow 2.0
编译器：Pycharm

第一部分：

1.1 问题：RuntimeError: tf.placeholder() is not compatible with eager execution.

当运行中报错：RuntimeError: tf.placeholder() is not compatible with eager execution.

RuntimeError: tf.placeholder() is not compatible with eager execution.

只需要在模型的最前面加上：

tf.compat.v1.disable_eager_execution()  # 禁用急切的执行
tf.compat.v1.reset_default_graph()  # 构建图

 

1.2 问题：No module named ‘tensorflow.examples.tutorials’

No module named 'tensorflow.examples.tutorials'

解决方法：
值得注意的是在Tensorflow 2.0版本就没有了input_data的板块，需要在GitHub上下载。
链接: No module named ‘tensorflow.examples.tutorials’.
当你在下载该模块时，你不必下载整个GItHub项目，而只用下载tutorials文件夹，可以在谷歌浏览器下安装Git Zip来实现只用下载GItHub整个项目下的单个文件夹的内容。

 

1.3 问题：tf.compat.v1.***

为确保高版本的TF支持低版本的TF代码，升级脚本加入了 compat.v1 模块。此模块将以等效的 tf.compat.v1.foo 引用代替表单 tf.foo 的调用。不过，建议您手动检查此类替代方案，并尽快将其迁移至 tf.* 命名空间（代替 tf.compat.v1.* 命名空间）中的新 API。

例如：
tf.Session()  改为 tf.compat.v1.Session()
...
tf.reduce_mean()  改为 tf.compat.v1.reduce_mean()
...
tf.global_variables_initializer()  改为 tf.compat.v1.global_variables_initializer()
...

具体哪个模块可以调用哪些函数，可以参考：
Tensorflow 2.0官网 ：https://tensorflow.google.cn/versions/r2.0/api_docs/python/tf

 
 

第二部分：

本节通过一个简单的逻辑回归实例为读者展示深度学习的神奇。通过对代码的具体步骤。

案例描述
假设有一组数据集，其 $x$ 和 $y$ 的对应关系为$y\approx 2x$
本实例就是让神经网络学习这些样本，并能够找到其中的规律，即让神经网络能够总结出$y\approx 2x$ 这样的公式。

2. 1 准备数据

这部分主要的任务是生成离散的数据，这部分的数据的对应关系近似为$y\approx 2x$

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

train_x = np.linspace(-1, 1, 100)
train_y = 2 * train_x + np.random.randn(100) * 0.3  # 加入噪声

# 显示模拟的数据点
fig, axes = plt.subplots(1, 1)
plt.plot(train_x, train_y, 'ko', label='Original data')
plt.legend()
plt.show()

 

2. 2 搭建模型

模型的搭建分成两个方向：正向和反向。

（1）正向搭建模型
正向的过程可以理解为：输入x的值，初始化的w值，b值，进行正向的模型训练，得到输出z的过程。
于是可以写成：
　　　　　　　　　　　　　　　　　　　
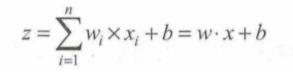
我们可以通过代码来进行分析：

# 创建模型
# 占位符
X = tf.compat.v1.placeholder("float")  # 为sess.run(optimizer, feed_dict={X:x, Y:y})不报错
Y = tf.compat.v1.placeholder("float")

# 模型参数
W = tf.Variable(tf.random.normal([1]), name="weight")
b = tf.Variable(tf.zeros([1]), name="bias")

# 前向结构
z = tf.multiply(X, W) + b

在正向开始前，定义了X.Y占位符，单位为1，维度为1。
定义了初始化参数W，b；正向的结构。

（2）反向搭建模型
反向的过程可以理解为：计算正向得到的值与真实值的差距cost， 再通过反向过程将里面的参数进行调整，接着再次正向生成预测值并与真实值进行比对，这样循环下去，直到将参数调整为合适值为止。

# 反向优化
cost = tf.reduce_mean(tf.square(Y - z))  # 生成值与真实值的平方差(3.3.6.2)
learning_rate = 0.01
optimizer = tf.compat.v1.train.GradientDescentOptimizer(learning_rate).minimize(cost)  #梯度下降 对应课本（3.3.7）

 

2. 3 迭代训练模型

建立好模型后， 可以通过法代来训练模型了。 TensorFlow 中的任务是通过 session 来进行的。

我认为在tensorflow中的任务都是通过session来训练的，大到复杂的神经网络，小到1+1。

先进行全局初始化，然后设置训练法代的次数， 启动 session 开始运 行任务。

# 训练模型
# 初始化所有变量
init = tf.compat.v1.global_variables_initializer()
# 定义参数
training_epochs = 30  # 设置迭代次数
display_step = 2
var_w = []
var_b = []

# 启动session
with tf.compat.v1.Session() as sess:
    sess.run(init)
    plotdata = {"batchsize":[],
                "loss":[]}  # 存放批次值和损失值
    # 向模型输入数据
    for epoch in range(training_epochs):
        for (x, y) in zip(train_x, train_y):
            sess.run(optimizer, feed_dict={X:x, Y:y})
        # 显示详细信息
        if epoch % display_step == 0:
            loss = sess.run(cost, feed_dict={X:train_x, Y:train_y})
            print("Epoch:", epoch+1, "cost=", loss,
                  "W=", sess.run(W), "b=", sess.run(b))
            if not (loss == "NA") :
                plotdata["batchsize"].append(epoch)
                plotdata["loss"].append(loss)
    print(" Finished! ")
    print("cost=", sess.run(cost, feed_dict={X:train_x, Y:train_y}),
          "W=", sess.run(W), "b=", sess.run(b))  # 课本（3.3.10）
    var_w = sess.run(W)
    var_b = sess.run(b)

    # 使用模型进行训练
    print("x=2, z=", sess.run(z, feed_dict={X: 0.2}))
    

上面的代码中迭代次数设置为 30 次，通过 sess.run 来进行网络节点的运算，通过 feed 机制将真实数据灌到占位符对应的位置（feed_dict={X: x, Y: y｝），同时，每执行一次都会将网络结构中的节点打印出来。
训练结果：

Epoch: 1 cost= 0.14914554 W= [1.5722855] b= [0.13340811]
Epoch: 3 cost= 0.093230814 W= [1.8432053] b= [0.06402624]
Epoch: 5 cost= 0.088043764 W= [1.9170187] b= [0.03628269]
Epoch: 7 cost= 0.087553866 W= [1.9361677] b= [0.02894412]
Epoch: 9 cost= 0.08748528 W= [1.9411201] b= [0.0270439]
Epoch: 11 cost= 0.087471426 W= [1.9424018] b= [0.02655203]
Epoch: 13 cost= 0.08746811 W= [1.9427323] b= [0.02642515]
Epoch: 15 cost= 0.08746727 W= [1.942818] b= [0.02639229]
Epoch: 17 cost= 0.08746706 W= [1.9428403] b= [0.02638376]
Epoch: 19 cost= 0.087467 W= [1.9428461] b= [0.02638153]
Epoch: 21 cost= 0.087466985 W= [1.942847] b= [0.02638116]
Epoch: 23 cost= 0.08746698 W= [1.9428475] b= [0.026381]
Epoch: 25 cost= 0.08746698 W= [1.9428475] b= [0.02638099]
Epoch: 27 cost= 0.08746698 W= [1.9428475] b= [0.02638099]
Epoch: 29 cost= 0.08746698 W= [1.9428475] b= [0.02638099]
 Finished! 
cost= 0.08746698 W= [1.9428475] b= [0.02638099]

可以看出， cost 的值在不断地变小， w 和 b 的值也在不断地调整。

（1）可视化图像

# 训练模型可视化
def moving_average(a, w=10):
    if len(a) < w:
        return a[:]
    return [val if idx < w else sum(a[(idx-w):idx])/w for idx,val in enumerate(a)]


# 图像显示
plt.figure()
plt.plot(train_x, train_y, 'ko', label='Original data')
plt.plot(train_x, float(var_w[0]) * train_x + float(var_b[0]), 'ro', label='Fitted_line')  # 通过函数值绘图
plt.legend()
plt.show()

plt.figure()  # 增加一个画布
plt.subplot(212)
plotdata["avgloss"] = moving_average(plotdata["loss"])
plt.plot(plotdata["batchsize"], plotdata["avgloss"], 'b--')
plt.xlabel("Minibatch number")
plt.ylabel("loss")
plt.title("Minibatch run vs. Training loss")
plt.show()

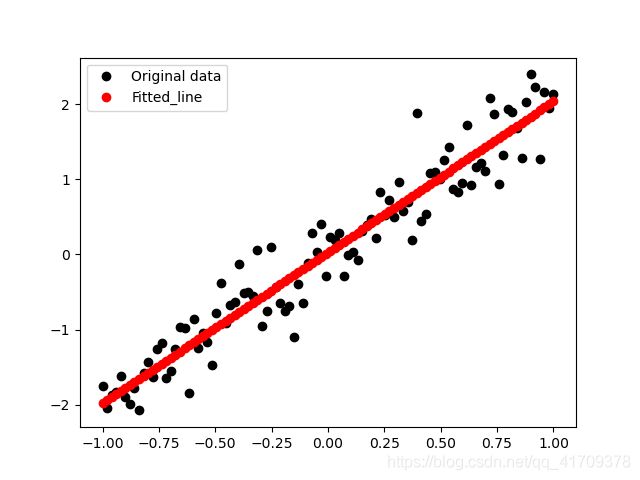
上图中所示的斜线， 是模型中的参数 w 和 b 为常量所组成的关于 x 与y 的直线方程。 可以看到是一条几乎 y=2x 的直线（W=1.94284753 接近于 2, b=0.02638099 接近于 0）。
　　　　　　　　　　　　　　　　　　　

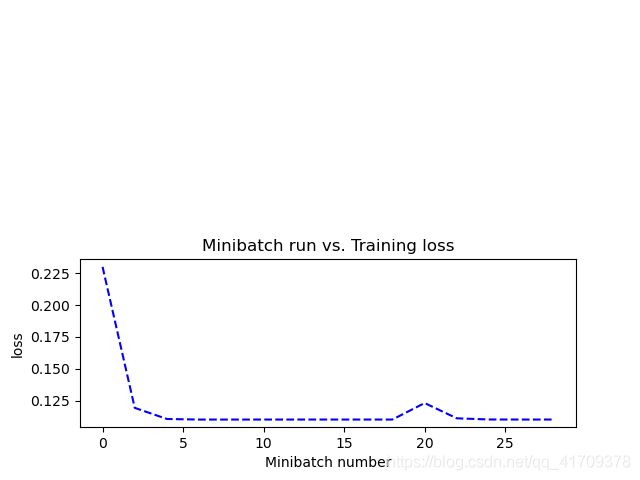
上图中可以看到刚开始损失值一直在下降，直到 6 次左右趋近平稳。
 

2. 4 使用模型

模型训练好后， 用起来就比较容易了，往里面传一个 0.2 (通过 feed_dict={X:0.2}) , 然后使用 sess.run 来运行模型中的 z 节点，使用模型，看看它生成的值。

    # 使用模型进行训练
    print("x=2, z=", sess.run(z, feed_dict={X: 0.2}))

输出结果：

x=2, z= [3.912076]

 

2. 5 保存／载入线性回归模型

（1）保存模型
首先需要建立一个 saver， 然后在 session 中通过 saver 的 save 即可将模型保存起来。 代码如下：

# 生成saver
saver = tf.compat.v1.train.Saver()
savedir = 'log/'  # 保存文件的路径
...
with tf.compat.v1.Session() as sess:
...
    # 存储起来
    saver.save(sess, savedir+"linermodel.cpkt")  # 保存模型

（2）载入模型
将模型保存好以后，载入也比较方便。在 session 中通过调用 saver 的 restore() 函数， 会从指定的路径找到模型文件， 并覆盖到相关参数中。代码如下：

# 载入模型
with tf.compat.v1.Session() as sess2:
    sess2.run(init)
    saver.restore(sess2, savedir+"linermodel.cpkt")  # 载入模型
    print("x=0.2, z=", sess2.run(z, feed_dict={X: 0.2}))

 

2. 6 线性回归的 TensorBoard 可视化

下面举例演示 TensorBoard 的可视化效果。
实例描述 为“线性回归”代码文件添加支持输出 TensorBoard 信息的功能，演示通过 Tensor Board 来观察训练过程。
本例还是以“3-1 线性回归.py”文件的代码为原型，在上面添加支持 TensorBoard 的 功能。
该例子中 ，通过添加一个标量数据和一个直方图数据到 log 里，然后通过 TensorBoard 显示出来。 代码改动量非常小，第一步加入到 summary， 第二步写入文件。 将模型的生成值加入到直方图数据中，将损失值加入到标量数据中，代码如下：

#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @File  : 4-8tensorboard-linear-regression.py
# @Author: Stormzudi
# @Date  : 2020/8/5 14:16

"""
4.1.17 实例 13：线性回归的 TensorBoard 可视化
"""

#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @File  : 3-1Linear-regression.py
# @Author: Stormzudi
# @Date  : 2020/8/2 17:32


import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt


train_x = np.linspace(-1, 1, 100)
train_y = 2 * train_x + np.random.randn(100) * 0.3  # 加入噪声

# 显示模拟的数据点
fig, axes = plt.subplots(1, 1)
plt.plot(train_x, train_y, 'ko', label='Original data')
plt.legend()
plt.show()

# 创建模型
# 占位符
tf.compat.v1.disable_eager_execution()
X = tf.compat.v1.placeholder("float")  # 为sess.run(optimizer, feed_dict={X:x, Y:y})不报错
Y = tf.compat.v1.placeholder("float")

# 模型参数
W = tf.Variable(tf.random.normal([1]), name="weight")
b = tf.Variable(tf.zeros([1]), name="bias")

# 前向结构
z = tf.multiply(X, W) + b
tf.compat.v1.summary.histogram('z', z)  # 将预测值以直方图形式显示
# 反向优化
cost = tf.reduce_mean(tf.square(Y - z))  # 生成值与真实值的平方差(3.3.6.2)
tf.compat.v1.summary.scalar('loss_function', cost)  # 将损失以标量形式显示
learning_rate = 0.01
optimizer = tf.compat.v1.train.GradientDescentOptimizer(learning_rate).minimize(cost)  # 对应课本（3.3.7）

# 训练模型
# 初始化所有变量
init = tf.compat.v1.global_variables_initializer()
# 定义参数
training_epochs = 30  # 设置迭代次数
display_step = 2


# 在启动 session 之后加入代码，创建一个 summary_writer
# 启动session
with tf.compat.v1.Session() as sess:
    sess.run(init)
    # 合并所有summary
    marge_summary_op = tf.compat.v1.summary.merge_all()
    # 创建summary_writer,用于写文件
    summary_writer = tf.compat.v1.summary.FileWriter('log/mnist_with_summaries', sess.graph)
    # 向模型输入数据
    for epoch in range(training_epochs):
        for (x, y) in zip(train_x, train_y):
            sess.run(optimizer, feed_dict={X:x, Y:y})
            # 生成summary
            summary_str = sess.run(marge_summary_op, feed_dict={X:x, Y:y})
            summary_writer.add_summary(summary_str, epoch)  # 将summary 写入文件
    print(" Finished! ")
    print("cost=", sess.run(cost, feed_dict={X:train_x, Y:train_y}),
          "W=", sess.run(W), "b=", sess.run(b))  # 课本（3.3.10）

运行代码，显示的内容和以前一样没什么变化， 来到生成的路径下可以看到多了一个文件，如图下图所示。
　　　　　　　　　　　　　　　　　　　
然后单击“开始”｜“运行”，输入 cmd， 启动“命 令行”窗口。首先来到 summary 日志的上级路径下， 输 入如下命令：

tensorboard --logdir F:\Python\Python_learning\Python_Deep_learning\TensorFlow-for-Deep-Learning-Book\Stormzudi\log\mnist_with_summaries

结果如图所示。

接着打开 Chrome 浏览器，输入 http://localhost:6006/， 会看到如下图所示界面。单击 SCALARS，会看到之前创建的 loss fuction。这个 loss fuction 也是可以点开的，点开 后可以看到损失值随选代次数的变化情况，如下图所示。

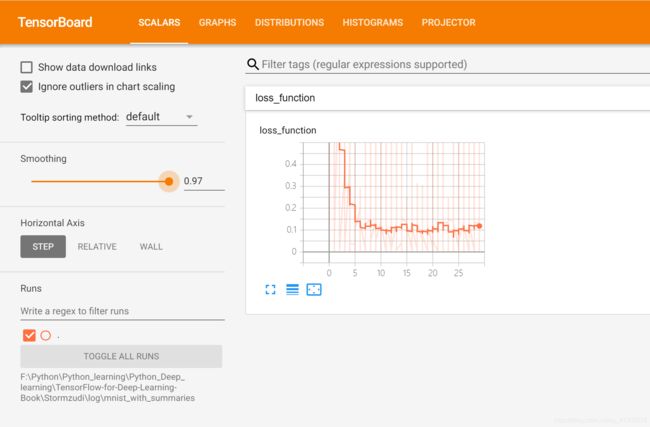
值得注意的是，如果mnist_with_summaries文件夹下有多个LAPTOP-INPKIV6T文件时，绘制出的loss_fuction图形的线条会叠加。

 
第二部分中完整的代码，可以移步到Github ： https://github.com/Stormzudi/Python-Data-Mining
 
 

第三部分：

本章中将训练一个能够识别图片中手写数字的机器学习模型。这个模型很简单，仅使 用了一个神经元 - Softmax Regression。

本章实例中所用的图片来源于一个开源的训练数据集-MNIST。
实例描述从MNIST 数据集中选择一幅图，这幅图上有一个手写的数字，让机器模拟人眼来区 分这个手写数字到底是几。 首先来介绍一下编写代码的相关步骤。
(1) 导入 NMIST 数据集
(2) 分析 MNIST 样本特点定义变量
(3) 构建模型
(4) 训练模型并输出中间状态参数
(5) 测试模型
(6) 保存模型
(7) 读取模型

3. 1 准备数据

MNIST数据集的官网是 http://yann.lecun.com/exdb/mnist/， 读者可以在这里面手动下载数据集。

（1）MNIST数据集的组成
链接: 详解 MNIST 数据集：https://www.cnblogs.com/xianhan/p/9145966.html
　　　　　　　　　　　　　　　　　　　
在 MNIST训练、数据集中 ，mnist.train.images是一个形状为［55000,784］的张量。其中， 第1个维度数字用来索引图片，第 2 个维度数字用来索引每张图片中的像素点。 此张量里 的每一个元素，都表示某张图片里的某个像素的强度值， 值介于 0～255 之间。 MNIST 里包含 3 个数据集： 第一个是训练数据集，另外两个分别是测试数据集 ( mnist.test） 和验证数据集（ mnist. validation ）

（2）读取MNIST数据集

# 引入input_data方法
from tensorflow_core.examples.tutorials.mnist import input_data
# 读取数据
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)

值得注意的是在Tensorflow 2.0版本就没有了input_data的板块，需要在GitHub上下载。
链接: No module named ‘tensorflow.examples.tutorials’.
当你在下载该模块时，你不必下载整个GItHub项目，而只用下载tutorials文件夹，可以在谷歌浏览器下安装Git Zip来实现只用下载GItHub整个项目下的单个文件夹的内容。

 

3. 2 搭建模型

（1）定义变量
由于输入图片是个 550000× 784 的矩阵，所以先创建一个[None,784］的占位符 x 和一 个[None,10］的占位符 y，然后使用 feed 机制将图片和标签输入进去。具体代码如下。

import pylab
import tensorflow as tf
from tensorflow_core.examples.tutorials.mnist import input_data

# 读取数据
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)

# 5.2 分析图片的特点，定义变量
tf.compat.v1.disable_eager_execution()  # 禁用急切的执行
tf.compat.v1.reset_default_graph()  # 构建图
# 定义占位符
x = tf.compat.v1.placeholder(tf.compat.v1.float32, [None, 784])  # MNIST数据集的维度为28*28 = 784
y = tf.compat.v1.placeholder(tf.compat.v1.float32, [None, 10])  # MNIST数据集的维度为28*28 = 784

（2）定义学习参数
在这里赋予 tf.Variable 不同的初值来创建不同的参数。 一般将 W 设为一个随机值， 将 b 设为 0。

W 的维度是［784, 10］，因为想要用 784 维的图片向量来以它，以得到一个 10 维 的证据值向量，每一位对应不同数字类。 b 的形状是［10］，所以可以直接把它加 到输出上面。

# 5.3 构建模型
W = tf.compat.v1.Variable(tf.compat.v1.random_normal(([784, 10])))
b = tf.compat.v1.Variable(tf.compat.v1.zeros([10]))

（3）定义输出节点
首先，用 tf.matmul(x, W）表示 x 乘以 W，这里 x 是一个二维张量，拥有多个输入。
然后再加上 b，把它们的和输入到 tf.nn.softmax 函数里。

# 5.3.2 定义输出节点
pred = tf.compat.v1.nn.softmax(tf.compat.v1.matmul(x, W) + b)  # Softmax分类

（4）定义反向传播的结构

# 5.3.3 定义反向传播的结构
# 损失函数
cost = tf.compat.v1.reduce_mean(-tf.compat.v1.reduce_sum(y*tf.compat.v1.log(pred), reduction_indices=1))
# 定义参数
learning_rate = 0.01
# 使用梯度下降优化器
optimizer = tf.compat.v1.train.GradientDescentOptimizer(learning_rate).minimize(cost)

1 将生成的 pred 与样本标签 y 进行一次交叉熵的运算，然后取平均值。
2 将这个结果作为一次正向传播的误差，通过梯度下降的优化方法找到能够使这个 误差最小化的 b 和 W 的偏移量。
3 更新 b 和 W，使其调整为合适的参数。

整个过程就是不断地让损失值（误差值 cost）变小。因为损失值越小，才能表明输出 的结果跟标签数据越相近。当 cost 小到我们的需求时，这时的 b 和 W 就是训练出来的合 适值。

 

3. 3 迭代训练模型

（1）训练模型
参数定义好后， 启动一个 session 就可以开始训练过程了。 session 中有两个 run， 第一 个 run 是运行初始化， 第二个 run 是运行具体的运算模型。模型运算之后便将里面的状态打印出来。

（2）测试模型
与前面的过程类似， 也是先将计算测试的网络结构建立起来， 然后通过最终节点的 eval 将测试值运算出来。

测试错误率的算法是： 直接判断预测的结果与真实的标签是否相同，如是相同的就表 明是正确的，如是不相同的就表示是错误的 。然后将正确的个数除以总个数，得到的值即 为正确率。

由于是 onehot 编码， 这里使用了 tf.argmax 函数返回 onehot 编码中数值为 1 的 那个元素的下标。下面是具体代码。

# 5.4 训练模型并输出中间状态参数
training_epochs = 25
batch_size = 100
display_step = 1

# 生成saver
saver = tf.compat.v1.train.Saver()
model_path = 'log/521model.ckpt'  # 保存文件的路径

# 启动session
with tf.compat.v1.Session() as sess:
    # 初始化
    sess.run(tf.compat.v1.global_variables_initializer())

    # 启动循环开始训练
    for epoch in range(training_epochs):
        avg_cost = 0
        total_batch = int(mnist.train.num_examples/batch_size)
        # 循环所有的数据集
        for i in range(total_batch):
            batch_xs, batch_ys = mnist.train.next_batch(batch_size)
            # 运行优化器
            _, c = sess.run([optimizer, cost], feed_dict={x: batch_xs, y:batch_ys})

            # 计算平均loss值
            avg_cost += c / total_batch
        # 显示训练中的详细信息
        if (epoch + 1) % display_step == 0:
            print("Epoch:", '%04d' % (epoch+1), "cost=","{:.9f}".format(avg_cost))
    print("Finished!")

    # 测试model
    correct_prediction = tf.compat.v1.equal(tf.compat.v1.argmax(pred, 1), tf.compat.v1.argmax(y, 1))
    # 计算准确率
    accuracy = tf.compat.v1.reduce_mean(tf.compat.v1.cast(correct_prediction, tf.compat.v1.float32))
    print("Accuracy:", accuracy.eval({x: mnist.test.images, y:mnist.test.labels}))

    # 保存模型
    save_path= saver.save(sess, model_path)
    print("Model saved in file :%s" % save_path)

结果：

Epoch: 0001 cost= 7.801266705
Epoch: 0002 cost= 3.816817245
Epoch: 0003 cost= 2.682076286
Epoch: 0004 cost= 2.179933401
Epoch: 0005 cost= 1.886112211
Epoch: 0006 cost= 1.690003775
Epoch: 0007 cost= 1.548772575
Epoch: 0008 cost= 1.441451006
Epoch: 0009 cost= 1.356609245
Epoch: 0010 cost= 1.287528893
Epoch: 0011 cost= 1.229882054
Epoch: 0012 cost= 1.180832165
Epoch: 0013 cost= 1.138436841
Epoch: 0014 cost= 1.101381120
Epoch: 0015 cost= 1.068324852
Epoch: 0016 cost= 1.038966936
Epoch: 0017 cost= 1.012414241
Epoch: 0018 cost= 0.988175549
Epoch: 0019 cost= 0.966231192
Epoch: 0020 cost= 0.945914678
Epoch: 0021 cost= 0.927081019
Epoch: 0022 cost= 0.909812384
Epoch: 0023 cost= 0.893629965
Epoch: 0024 cost= 0.878600785
Epoch: 0025 cost= 0.864478832
Finished!
Accuracy: 0.8263
Model saved in file :log/521model.ckpt

这里输出的中间状态是 cost 损失值。读者也可以把 自己关心的内容打印出来。 可以看 到，从第 1 次迭代到第 25 次法代的损失值在逐渐减小， 最终的误差只有 0.8645。

上面代码执行后， 显示信息如下：

Accuracy: 0.8263

测试正确率的算法与损失值的算法略有差别，但代表的意义却很类似。当然，也可以直接拿计算损失值的交叉娟结果来代表模型测试的错误率。
 

3. 4 使用模型

（1）保存模型
首先要建立一个 saver 和一个路径，然后通过调用 save，自动将 session 中的参数保存 起来，见如下代码。

# 生成saver
saver = tf.compat.v1.train.Saver()
model_path = 'log/521model.ckpt'  # 保存文件的路径

# 启动session
with tf.compat.v1.Session() as sess:
...
    # 保存模型
    save_path= saver.save(sess, model_path)
    print("Model saved in file :%s" % save_path)
...

（2）读取模型
将模型存储好后，下面来做一个实验：读取模型井将两张图片放进去让模型预测结果， 然后将两张图片极其对应的标签一井显示出来。
在整个代码执行过程中，对于网络模型的定义不变，只是重新建立一个 session 而己， 所有的操作都在这个新的 session 中完成。具体细节几代码。

# 5.7 读取模型进行验证
print("Starting 2nd session ...")
with tf.compat.v1.Session() as sess:
    # 初始化变量
    sess.run(tf.compat.v1.global_variables_initializer())
    # 恢复模型变量
    saver.restore(sess, model_path)

    # 测试 model
    correct_prediction = tf.compat.v1.equal(tf.compat.v1.argmax(pred, 1), tf.compat.v1.argmax(y, 1))
    # 计算准确率
    accuracy = tf.compat.v1.reduce_mean(tf.compat.v1.cast(correct_prediction, tf.compat.v1.float32))
    print("Accuracy:", accuracy.eval({x: mnist.test.images, y:mnist.test.labels}))

    out_put = tf.compat.v1.argmax(pred, 1)
    batch_xs, batch_ys = mnist.train.next_batch(2)  # 需要预测的个数:num = 3
    outputval, predv = sess.run([out_put, pred], feed_dict={x:batch_xs})
    print(outputval, predv, batch_ys)

    # 展示图像
    im = batch_xs[0]
    im = im.reshape(-1, 28)
    pylab.imshow(im)
    pylab.show()

    im = batch_xs[1]
    im = im.reshape(-1, 28)
    pylab.imshow(im)
    pylab.show()

结果：

Starting 2nd session ...
Accuracy: 0.8263
[9 7] [[4.7544941e-09 1.5396923e-12 1.3169211e-08 2.3234898e-08 1.3510973e-02
  2.7141198e-06 5.1582216e-08 2.0368865e-02 2.0078753e-06 9.6611542e-01]
 [1.4170609e-09 1.6089351e-05 3.7409162e-08 8.9374544e-06 3.4157737e-04
  5.3770259e-07 1.1696112e-09 9.7058982e-01 2.8268071e-02 7.7500142e-04]] [[0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]
 [0. 0. 0. 0. 0. 0. 0. 1. 0. 0.]]

　　　　　　　　　　　　　　　　　　　
分析上面的结果可以看到：outputval为预测的数字，predv中每个数对应的是一个向量，向量的和为1，这个向量是通过softmax转换而成，向量中最大数的位置就是预测的这个数，于是predv中的数据0-1化后就变成了原本batch_ys的数据。