NTT Masque: 多风格生成式阅读理解（Multi-Style Generative Reading Comprehension）

【Reference】
1. Multi-Style Generative Reading Comprehension
2. 论文笔记–Multi-Style Generative Reading Comprehension (Masque)

---

截止2020年8月21日，本文提出的Masque模型是在MS MARCO和NarrativeQA数据集上表现最好的模型。

RC研究领域多使用范围抽取式方法，生成式方法面临开放领域训练数据匮乏。本文提出多风格问答阅读理解摘要模型，从问句和多个段落生成指定风格的summary作为答案。

• 多源摘要： 使用指针生成器机制从问句、多段落中生成多样化风格的答案，并扩展至Transformer，允许生成器从词表，或从问句、段落原文中以复制方式生成答案；
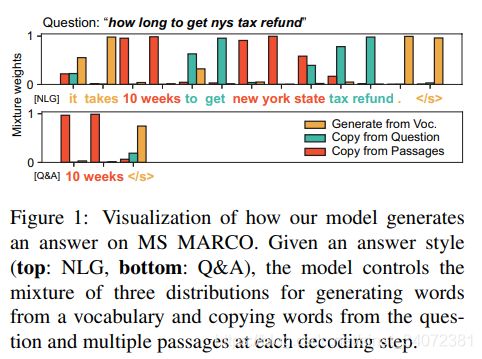
• 多风格学习： 控制答案输出样式，满足RC所有形式输出，引入风格化的人工token扩展指针生成器为条件解码器，给定风格下，每一步解码控制三个分布占解码输出的权重；

问题形式化

给定含$J$个单词的问句$x^q=\{x_1^q,\cdots ,x_J^q\}$，$K$个段落，其中第$k$个段落包含$L$个单词，表示为$x^{p_k}=\{x_1^{p_k},\cdots ,x_L^{p^k}\}$，风格标签$s$，RC模型输出答案$y=\{y_1,\cdots ,y_T\}$。

模型简化为：给定三元组$(x^q,\{x^{p_k}\},s)$，模型预测输出$P(y)$。训练数据具有6个三元组：$(x^q,\{x^{p_k}\},s,y,a,\{r^{p_k}\})$，其中$a$和$\{r_{p_k}\}$可选，$a=1$表示问句可以回答，$r^{p_k}=1$表示段落对回答问句有效。

提出的模型

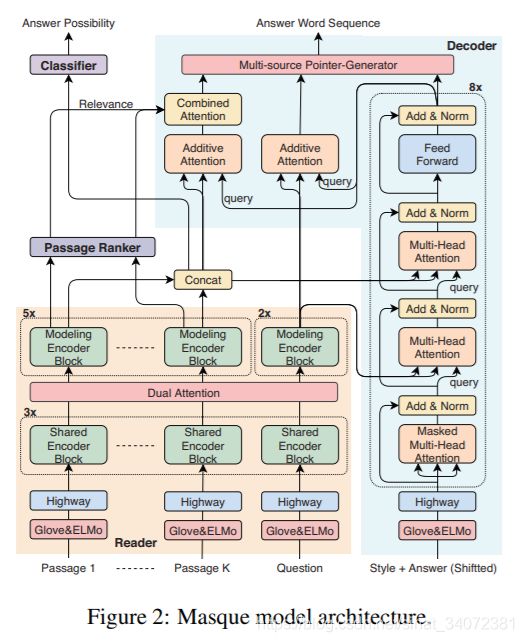
多风格问答摘要模型 Masque，直接建模条件概率$p(y|x^q,\{x^{p_k}\},s)$，模型结构如上，包含：

• 问句-段落阅读器，建模问句和段落之间的交互；
• 段落排序，找到与问句相关的段落；
• 可问答二分类器，识别问句是否可回答；
• 答案句编码器，输出给定风格下的答案；

模型基于多任务学习：段落排序、可回答二分类器、NLG，NLG的学习具有风格独立性，并可将其输出转化为目标风格。

问句-段落阅读器（Question-Passages Reader）

词向量层

分别得到问句和段落中各词的预训练Glove词向量和具有上下文表示的ELMo词向量，使用两层Highway Network（问句和段落参数共享）融合两种词向量。

共享编码层

使用问句和段落各词在堆叠Transformer的顶层输出作为各单词的词向量表示，首层是将词向量线性变换$d$维，编码器共享层输出段落词向量$E^{p_k}\in {\mathbb{R}}^{d\times L}$和问句词向量$E^q\in {\mathbb{R}}^{d\times J}$。

编码器块由两个子层构成：多头自注意力层和位置感知前馈网络层。

与GPT模型一致，前馈网络由使用GELU激活函数连接的两层线性网络构成。每个子层内部使用残差连接（所有子层网络输出维度均为$d$维）和层标准化，如给定输入$x$和子层网络函数$f$，则子层网络输出$\text{LN}(f(x)+x)$。

由于词向量使用ELMo词向量，本身具有位置信息，因此本文模型中不使用位置嵌入。

双重注意力

使用双重注意力，融合问句表示和段落表示的彼此信息。

首先计算问句和每个段落的相似度矩阵$U^{p_k}\in {\mathbb{R}}^{L\times J}$，其中第$k$个段落的第$l$个单词与问句的第$j$个单词的相似度为
$$U_{ij}^{p_k}=w^{q\top }[E_l^{p_k};E_j^q;E_l^{p_k}\odot E_j^q]$$
参数$w^a\in {\mathbb{R}}^{3d}$，$\odot$表示Hadamard product（对应元素相乘），$;$表示按行拼接。接着按行标准化（段落不同单词对问句同一单词的注意力）相似矩阵、按列标准化（问句不同单词对段落同一单词的注意力）相似矩阵：
$$A^{p_k}={\text{softmax}}_j(U^{p_k\top }),B^{p_k}={\text{softmax}}_l(U^{p_k})$$

使用Dynamic Coattention Networks, DCN，获取段落词向量的双重注意力表示$G^{q\to p_k}\in {\mathbb{R}}^{5d\times L}$，问句词向量的双重注意力表示$G^{p\to q}\in {\mathbb{R}}^{5d\times J}$：
$$\begin{array}{rl}{G}^{q\to p_k}& =[E^{p_k};{\bar{A}}^{p_k};{\hat{A}}^{p_k};E^{p_k}\odot {\bar{A}}^{p_k};E^{p_k}\odot {\hat{A}}^{p_k}]\\ G^{p\to q}& =[E^q;\bar{B};\hat{B};E^q\odot \bar{B};E^q\odot \hat{B}]\end{array}$$

以下各矩阵列向量的含义：

• $E^{p_k}$，段落各位置词向量；
• ${\bar{A}}^{p_k}=E^q{A}^{p_k}$，段落各位置attention的问句词向量；
• ${\bar{B}}^{p_k}=E^{p_k}{B}^{p_k}$，问句各位置attention的段落词向量；
• ${\hat{A}}^{p_k}={\bar{B}}^{p_k}{A}^{p_k}$，段落各位置attention的段落词向量，即根据问句信息融入上下文信息的段落词向量；
• ${\hat{B}}^{p_k}={\bar{A}}^{p_k}{B}^{p_k}$，问句各位置attention的问句词向量，即根据段落信息融入上下文信息的问句词向量；
• $\bar{B}={\max }_k{\bar{B}}^{p_k}$，问句各位置的最大池化不同段落的段落词向量；
• $\hat{B}={\max }_k{\hat{B}}^{p_k}$；问句各位置的最大池化不同段落的问句词向量；

建模编码层

使用堆叠的5层和2层的Transformer编码块分别作为段落、问句编码器，编码段落词向量表示$M^{p_k}\in {\mathbb{R}}^{d\times L}$，问句词向量表示$M^q\in {\mathbb{R}}^{d\times J}$。$M^q$和$M^{p_k}$用于答案解码，$\{M^{p_k}\}$用于段落排序和可问答分类。

段落排序（Passage Ranker）

各段落词向量表示为$\{M^{p_k}\}$，使用各分段的第一个单词词向量$M_1^{p_k}$作为分段词向量表示，引入参数向量$w^r\in {\mathbb{R}}^d$，计算各段落与问句的相关性：
$${\beta }^{p_k}=\text{sigmoid}(w^{r\top }{M}_1^{p_k})$$

可问答分类器（Answer Possibility Classifier）

同样使用$M_1^{p_k}$作为各分段词向量表示，拼接各分段词向量表示作为分类器输入，引入参数向量$w^{c\top }\in {\mathbb{R}}^{Kd}$，计算可问答概率：
$$P(a)=\text{sigmoid}(w^{c\top }[M_1^{p_1};\cdots ;M_1^{p_K}])$$

答案句解码器（Answer Sentence Decoder）

解码器以自回归形式，使用上一步结果产生当前步输出。

词向量层

除使用单向ELMo之外（对未来位置信息位置），解码器词向量层与阅读器词向量层具有相同结构。

为满足生成不同风格答案，解码器使用与风格有关的token作为初始输入，产生对应风格输出，此外，解码器引入初始风格化标记，可避免阅读器依赖于风格化答案。

注意力解码器层

使用堆叠Transformer解码器块作为解码器层，首先将输入线性变换至$d$维，输出$d$维序列$\{s_1,\cdots ,s_T\}$。

除编码器块中的两个子层之外，解码器块在两个子层之间，额外引入第二、三子层。自注意力层使用后向序列mask避免解码时看见未来信息，第二、三子层为多头注意力层，分别使用$M^q$和$M^{p_{all}}$作为输入，其中：
$$M^{p_{all}}=[M^{p_1},\cdots ,M^{p_K}]\in {\mathbb{R}}^{d\times KL}$$

多源指针生成器

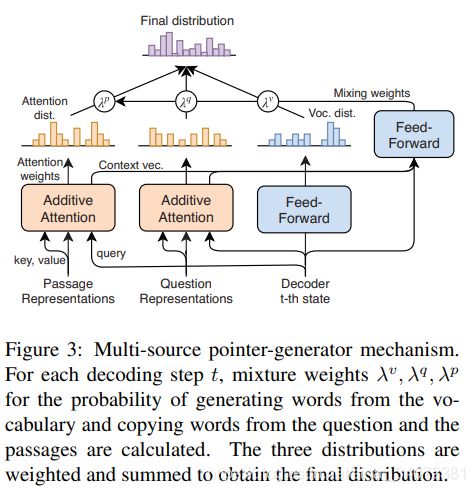
扩展生成机制，使得可从词典或从问句、多段落原文复制生成单词，我们希望复制机制能够共享答案风格。

多元分布生成简述：解码器顶层输出隐状态作为查询向量，输入至段落和问句注意力层，产生两个上下文向量和注意力权重，注意力权重作为复制分布输出概率，上下文向量用于计算复制分布在混合分布的权重。

扩展词典分布
将词典中常见单词，以及输入问句和段落原文单词，组合为扩展词典$V_{\text{ext}}$，则问答句第$t$单词概率：
$$P^v(y_t)=\text{softmax}(W^{2\top }(W^1{s}_t+b^1))$$

式中输出嵌入矩阵$W^2\in {\mathbb{R}}^{d_{\text{word}}\times V_{\text{ext}}}$是输入词向量矩阵的子集，参数$W^1\in {\mathbb{R}}^{d_{\text{word}}\times d}$，$b^1\in {\mathbb{R}}^{d_{\text{word}}}$。当$y_t$为OOB时，输出概率为0。

复制分布
基于Transformer的Ptr-Net任意选择注意力头产生复制分布，对摘要无显著改进，我们向解码器顶层的复制分布添加注意力层，如对于所有段落，将解码器输出$s_t$作为注意力查询向量，输出注意力权重${\alpha }_t^p\in {\mathbb{R}}^{KL}$，上下文向量$c_t\in {\mathbb{R}}^d$：
$$\begin{array}{rl}{e}_l^{p_k}& =w^{p\top }\tanh (W^{pm}{M}_l^{p_k}+W^{ps}{s}_t+b^p)\\ {\alpha }_t^p& =\text{softmax}([e^{p_1};\cdots ;e^{p_K}])\\ c_t^p& =\sum _l{\alpha }_{tl}^p{M}_l^{p_{all}},l=1,\cdots ,KL\end{array}$$
式中，参数$w^p,b^p\in {\mathbb{R}}^d$，$W^{pm},W^{ps}\in {\mathbb{R}}^{d\times d}$。

对于问句，使用同样结构的注意力层输出${\alpha }_t\in {\mathbb{R}}^J$，$c_t^q\in {\mathbb{R}}^d$，从而得到在扩展词汇的两个分布：
$$P^q(y_t)=\sum _{j:x_j^q=y_t}{\alpha }_{tj}^q,P^p(y_t)=\sum _{l:x_l^{p_{k(l)}}=y_t}{\alpha }_{tl}^p$$
式中，$k(l)$表示拼接所有段落得到的序列的第$l$个单词。

最终分布
使用三个分布的混合作为最终分布：
$$P(y_t)={\lambda }^v{P}^v(y_t)+{\lambda }^q{P}^q(y_t)+{\lambda }^p{P}^p(y_t),{\lambda }^{v,q,p}=\text{softmax}(W^m[s_t;c_t^q;c_t^p]+b^m)$$
式中，参数$W^m\in {\mathbb{R}}^{3\times 3d}$，$b^m\in {\mathbb{R}}^3$。

联合注意力
为使得不对不相关片段产生注意力，我们对段落单词注意力重新定义：
$${\alpha }_{tl}^p=\frac{{\alpha }_{tl}^p{\beta }^{p_{k(l)}}}{{\sum }_{l^{\prime }}{\alpha }_{t{l}^{\prime }}^p{\beta }^{p_{k(l^{\prime })}}}$$

损失函数

训练损失
$$L(\theta )=L_{\text{dec}}+{\gamma }_{\text{rank}}{L}_{\text{rank}}+{\gamma }_{\text{cls}}{L}_{\text{cls}}$$
式中，$\theta$是所有参数，${\gamma }_{\text{rank}}$，${\gamma }_{\text{cls}}$是平衡参数。解码损失$L_{\text{dec}}$使用所有可回答样本的平均负对数似然：
$$L_{\text{dec}}=-\frac{1}{N_{\text{able}}}\sum _{(a,y)\in \mathcal{D}}\frac{a}{T}\sum _t\log P(y_t)$$

分段排序和可回答二分类器损失使用所有样本真实值和预测值的交叉熵：
$$\begin{array}{rl}{L}_{\text{rank}}& =-\frac{1}{NK}\sum _k\sum _{r^{p_k}\in \mathcal{D}}(r^{p_k}\log {\beta }^{p_k}+(1-r^{p_k}\log (1-{\beta }^{p_k})))\\ L_{\text{cls}}& =-\frac{1}{N}\sum _{a\in \mathcal{D}}(a\log P(a)+(1-a)\log (1-P(a)))\end{array}$$

附录：实验数据

• batch_size:80;
• hidden_size d: 304;
• num_heads: 8;
• ffn_inner_state_size: 256;
• num_layers: shared encoding blocks, modeling blocks for a question, modeling blocks for passages, and decoder blocks were 3, 2, 5, and 8;
• embedding_size: Glove 300, ELMo 512 lowercased;
• V_ext: 5000;
• seq_len: passages and question 100;
• optiimizer: Adam beta₁ 0.9, beta₂ 0.008 eps 1e-8, learning rate 0 -> 2.5e-4 (2,000 steps) -> 0, exponential moving average decay rate 0.9995;
• initializer: N(0, 0.02) for kernel, Zeros for bias;
• regularization: dropout rate 0.3, L₂ w 0.01, smoothed positve labels to 0.9;

8块P100 GPU在MS MARCO数据集上跑8个epochs大概6天。