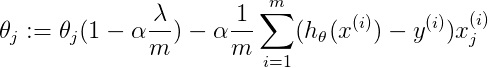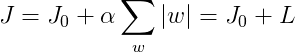正则化
目录
Batch_Size
需要Batch_Size的理由
在合理范围内,增大Batch_Size好处
盲目增大Batch_Size的坏处
归一化
归一化的作用
归一化的类型
批归一化BatchNormalization
为什么需要归一化
BN层及使用位置
批归一化BN的优点
批归一化BN的缺点
批归一化算法流程
Weight Normalizaition和Batch Normalization
BN的训练和预测
L1/L2范数正则化
实现参数稀疏的好处
参数越小代表模型越简单的原因
L2正则化可以获得较小的参数的原因
L1和L2正则化防止过拟合的原因
L1正则化产生稀疏权值矩阵的原因
L1正则化不可导的处理方法
Bagging和Dropout
Bagging集成方法
Dropout策略
Dropout可以解决过拟合的原因
Dropout与Bagging的不同
Batch_Size
需要Batch_Size的理由
Batch的选择,首先决定的是下降的方向。
如果数据集比较小,FullBatch Learning,好处是:
1、更好地代表样本总体,从而更准确地朝向极值所在的方向。
2、由于不同权重的梯度值差别巨大,因此选取一个全局的学习率很困难。可以使用Rprop(弹性反向传播)只基于梯度符号并且针对性单独更新各权值。
对于更大的数据集,FullBatch Learning,坏处是:
1、内存限制。
2、以Rprop的方式迭代,会由于各个Batch之间的采样差异性,各次梯度修正值相互
抵消,无法修正。这才有了后来RMSProp的妥协方案。
在合理范围内,增大Batch_Size好处
1、内存利用率提高,大矩阵乘法的并行化效率提高。
2、跑完一次epoch(全数据集)所需的迭代次数减少,处理速度加快。
3、在一定范围内,一般来说BatchSize越大,下降方向越准,引起训练震荡越小。
盲目增大Batch_Size的坏处
1、内存容量不足。
2、想达到相同的精度,所需epoch数量增大,花费时间增加,参数的修正更加缓慢。
3、BatchSize增大到一定程度,下降方向基本不再变化。
归一化
归一化的作用
(1)处理数据更加方便,可以避免数值问题。
(2)加快梯度下降的收敛速度。
(3)同一量纲。
(4)避免神经元饱和。
(5)保证输出数据中数值小的不被吞食。
归一化的类型
1)线性归一化
适用在数值比较集中的情况。
缺点:如果max和min不稳定,很容易使得归一化结果不稳定。
2)标准差归一化
3)非线性归一化
log,指数,正切
适用在数据分化较大的场景
批归一化BatchNormalization
为什么需要归一化
网络前面层训练参数的更新会导致后面层的输入数据分布发生变化,这种变化是累加的。BN的目的就是解决在训练过程中,中间层数据分布发生改变的情况。
BN层及使用位置
在网络的每一层输入之前,插入一个归一化层,即先进行归一化处理再进入网络的下一层。
CNN中BN一般应用在非线性激活函数之前,偏置参数b经过BN后是没有作用的,因为最后会被均值归一化,均值为0,方差为1。BN后面有个β偏置项。
批归一化BN的优点
1)减少了人为选择参数。在某些情况下可以取消dropout和L2正则项参数,或者采取更小的L2正则项约束参数;
2)减少了对学习率的要求。现在我们可以使用初始很大的学习率或者选择了较小的学习率,算法也能够快速训练收敛;
3)可以不再使用局部响应归一化。BN本身就是归一化网络
4)破坏原来的数据分布,一定程度上缓解过拟合
5)减少梯度消失,加快收敛速度,提高训练精度。
批归一化BN的缺点
1)批量统计估算不准确导致批量变小时,BN的误差会迅速增加。
2)在训练大型网络时,内存消耗限制了只能使用小批量的BN
BatchNormalization的缺点:
1、对BatchSize非常敏感。BatchNormalization的一个重要出发点是保持每层输入的数据同分布。回想下开始那个独立同分布的假设。假如取的batch_size很小,那显然有些Mini-Batch的数据分布就很可能与整个数据集的分布不一致了,又出现了那个问题,数据分布不一致,这就等于说没起到同分布的作用了,或者说同分布得不充分。实验也证明,batch_size取得大一点, 数据shuffle的好一点,BatchNormalization的效果就越好。
2、对RNN不适合。对所有样本求均值。对于图片这类等长的输入来说,这很容易操作,在每个维度加加除除就可以了,因为维度总是一致的。而对于不等长的文本来说,RNN中的每个time step共享了同一组权重。在应用BatchNormalization时,这就要求对每个time step的batch_size个输入计算一个均值和方差。那么问题就来了,假如有一个句子S非常长,那就意味着对S而言,总会有个time_step的batch_size为1,均值方差没意义,这就导致了BatchNormalization在RNN上无用武之地了。
批归一化算法流程
Weight Normalizaition和Batch Normalization
1、都属于参数重写的方法,只是采用的方式不同:
WN是对网络权值W进行归一化。
BN是对网络某一层输入数据进行归一化。
2、WN适用于RNN(LSTM)网络,未引进mini batch依赖。
3、BN基于一个mini batch的数据计算均值和方差,相当于进行梯度计算式引入噪声。
BN不能直接用于RNN,原因在于:
1)RNN 处理的Sequence是变长的;
2)RNN是基于time step计算,如果直接使用BN处理,需要保存每个time step下mini batch的均值和方差,效率低且占内存。
4、WN比BN引入更少的噪声,不需额外的空间保存均值,方差,开销小。
5、WN不具备BN把网络每一层的输出Y固定在一个变化范围的作用。WN需要特别注意参数初始值的选择
BN的训练和预测
1)训练时,每次会传入一批数据,算法如上图
2)预测时,每次可能只会传入单个数据,此时模型会使用全局统计量代替批统计量(移动平均);
训练每个batch时,都会得到一组(均值,方差),全局统计量,就是对这些均值和方差求其对应的数学期望;
面试问题:
为什么训练时不采用移动平均?
使用BN的目的就是为了保证每批数据的分布稳定,使用全局统计量反而违背了这个初衷;
BN的作者认为在训练时采用移动平均可能会与梯度优化存在冲突;
L1/L2范数正则化
L1正则化是指权值向量w中各个元素的绝对值之和,通常表示为||w||1
L2正则化是指权值向量w中各个元素的平方和然后再求平方根,通常表示为||w||2,我们让L2范数的规则项||W||2最小,可以使得W的每个元素都很小,都接近于0,不会等于0
L1/L2范数的异同
相同点:
限制模型的学习能力——通过限制参数的规模,使模型偏好于权值较小的目标函数,防止过拟合。
不同点:
1)L1正则化可以产生更稀疏的权值矩阵,可以用于特征选择,同时一定程度上防止过拟合;
L2正则化主要用于防止模型过拟合
2)L1正则化适用于特征之间有关联的情况;
L2正则化适用于特征之间没有关联的情况。
3)在线性回归模型中,L1正则化的模型叫做Lasso回归;L2正则化的模型叫做岭回归。
实现参数稀疏的好处
简化模型,避免过拟合;参数变少可以使整个模型获得更好的解释性
参数越小代表模型越简单的原因
因为复杂的模型会尝试对所有样本进行拟合,这其中就包含异常样本,容易造成在较小的区间里预测值产生较大的波动,这种较大的波动也反映了在这个区间里的导数很大,而只有较大的参数值才能产生较大的导数。因此复杂的模型,其参数值会比较大。
L2正则化可以获得较小的参数的原因
在梯度下降中,每次迭代![]() 要先乘以一个小于1的因子,使得
要先乘以一个小于1的因子,使得![]() 不断减少;
不断减少;![]() 就是正则化参数。
就是正则化参数。
L1和L2正则化防止过拟合的原因
1)通过限制模型参数的规模,来限制模型的学习能力;模型偏好于更小的权值,更低的模型复杂度,
2)模型对于噪声与异常点的抗干扰性的能力增强,从而提高模型的泛化能力。
L1正则化产生稀疏权值矩阵的原因
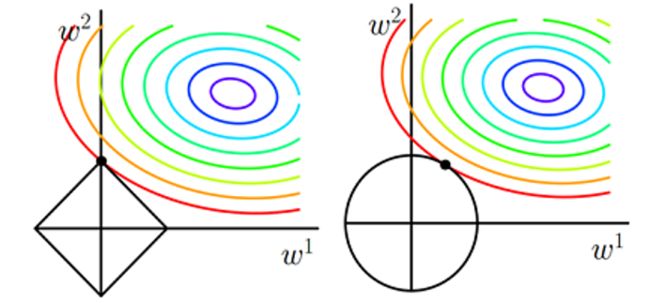
1)左边图L1正则化,假设有如下带L1正则化的损失函数:
等值线是J0的等值线,黑色方形是L函数的图形。在图中,当J0等值线与L图形首次相交的地方就是最优解。因为L函数有很多『突出的角』(二维情况下四个,多维情况下更多),J0与这些角接触的机率会远大于与L其它部位接触的机率,而在这些角上会有很多权值等于0,(注意这个顶点的值为(w1,w2)=(0,w))这就是为什么L1正则化可以产生稀疏模型,进而可以用于特征选择。
正则化前面的系数α,可以控制L图形的大小。α越小,L的图形越大(上图中的黑色方框);α越大,L的图形就越小,可以小到黑色方框只超出原点范围一点点
2)二维平面下L2正则化的函数图形是个圆,与方形相比,被磨去了棱角。因此J0与L相交时使得w1或w2等于零的机率小了许多,这就是为什么L2正则化不具有稀疏性的原因。
3)L1范数会使权值稀疏的原因:L1范数是L0范数的最优凸近似;任何的规则化算子,如果他在Wi=0的地方不可微,并且可以分解为一个“求和”的形式,那么这个规则化算子就可以实现稀疏。
L1正则化不可导的处理方法
1、坐标轴下降法
1)坐标轴下降法进行参数更新时,每次总是固定另外m-1个值,求另外一个的局部最优值,这样也避免了Lasso回归的损失函数不可导的问题。
2)坐标轴下降法每轮迭代都需要O(mn)的计算。(和梯度下降算法相同)
2、近端梯度下降(Proximal Gradient Descent)
Bagging和Dropout
Bagging集成方法
集成方法的主要想法是分别训练不同的模型,然后让所有模型表决最终的输出。
Bagging 是一种集成策略;具体来说,Bagging 涉及构造k个不同的数据集。
Dropout策略
Dropout 通过参数共享提供了一种廉价的 Bagging 集成近似;Dropout 策略相当于集成了包括所有从基础网络除去部分单元后形成的子网络。
通常,隐藏层的采样概率为 0.5,输入的采样概率为0.8;超参数也可以采样,但其采样概率一般为1。
Dropout可以解决过拟合的原因
(1)取平均的作用:dropout掉不同的隐藏神经元就类似在训练不同的网络,随机删掉一半隐藏神经元导致网络结构已经不同,整个dropout过程就相当于对很多个不同的神经网络取平均。而不同的网络产生不同的过拟合,一些互为“反向”的拟合相互抵消就可以达到整体上减少过拟合。
(2)减少神经元之间复杂的共适应关系:因为dropout程序导致两个神经元不一定每次都在一个dropout网络中出现。这样权值的更新不再依赖于有固定关系的隐含节点的共同作用,阻止了某些特征仅仅在其它特定特征下才有效果的情况。
(3)Dropout类似于性别在生物进化中的角色:物种为了生存往往会倾向于适应这种环境,环境突变则会导致物种难以做出及时反应,性别的出现可以繁衍出适应新环境的变种,有效的阻止过拟合,即避免环境改变时物种可能面临的灭绝。
Dropout与Bagging的不同
1)在Bagging的情况下,所有模型都是独立的;
在Dropout的情况下,所有模型共享参数,其中每个模型继承父神经网络参数的不同子集。
2)在Bagging的情况下,每一个模型都会在其相应训练集上训练到收敛。
在Dropout 的情况下,通常大部分模型都没有显式地被训练;取而代之的是,在单个步骤中我们训练一小部分的子网络,参数共享会使得剩余的子网络也能有好的参数设定。
最后如果转载,麻烦留个本文的链接,因为如果读者或我自己发现文章有错误,我会在这里更正,留个本文的链接,防止我暂时的疏漏耽误了他人宝贵的时间。