论文阅读-LightGBM: A Highly Efficient Gradient Boosting Decision Tree

GBDT是常用的机器学习算法，有少量高质量的实现算法，例如：XGBoost和pGBRT。当特征维度很高或者数据量很大时，在实现的工程优化算法中，效率和可扩展仍然不能满足得到满意的结果。主要的原因是对于每个特征，我们都需要去扫描整个数据集得到分割点，这个过程是非常耗时的。针对这个问题，我们提出了两种解决方法：基于梯度的one-side采样和互斥的特征捆绑。对于GOSS，我们排除了一部分梯度值小的数据实例，仅仅使用剩下来评估信息增益。这样做可行性的原因，拥有梯度值大的数据集在信息增益计算时扮演更重要的角色。在小数据集上GOSS可以获得更加准确的信息增益的评估结果。EFB捆绑互斥的特征，来减少特征的数量。但是我们发现最优的互斥特征是一个NP难问题，贪心算法可以取得近似的分数（在不损害分割点方向准确率的情况下，有效减少特征值）。

1 简介

GBDT因为其的有效性、准确性、可解释性，称为了广泛使用的机器学习算法。GBDT在众多的机器学习任务中取得了优越的结果，例如：多分类问题、点击预测、排序。随着大数据的出现，GBDT面临着些许挑战，特别是在准确率和效率之间的平衡。GBDT为了找到合适的分割点，需要扫描所有的数据。因此这个过程复杂度随着数据量和实例特征呈线性增长，所以在处理大数据时，这些实现方法需要大量的时间。为了应对如此的挑战，直接的想法就是在不影响准确率的情况下，减少数据量和特征，这个过程是复杂的，采样数据可能改变数据集的分布，有部分工作根据数据权重加速boosting训练过程，但是这不能直接应用于GDBT。

GOSS：前提是数据实例的梯度在信息增益上扮演者不同的作用，这个可以作为GBDT的权重，根据信息增益的定义，拥有大的梯度的实例贡献更多的信息增益，所以为了维持结果的准确性，我们应该尽量保留梯度大的实例，而舍弃梯度值小的实例。相比于均匀采样这种权重处理技巧能够获得更加准确的结果，特别是在数据量大的时候。

EFB：在真是的应用中，高维度特征具有稀疏性，这样可以设计一个减少有效特征数量的无损的方法，特别是在稀疏特征中，许多特征是互斥的，出现大量0，例如one-hot。我们可以捆绑互斥的特征。最后我们还原捆绑互斥问题为图着色问题，使用贪心算法近似求解。

基于上述两点的lightGBM取得了很好的结果，文章的结构，GBDT 现状、GOSS、EFB、实验结果。

2 GBDT工作

2.1 GBDT和复杂度分析

GBDT是决策树的集成模型，按顺序训练。在每次迭代过程中，GBDT通过拟合负梯度（残差）学到决策树。

GBDT主要的时间花销是学习决策树，学习决策树中的主要工作是找到分割点。被大家广泛采用的算法是通过预排序找到分割点，这种方法列举于预排序中所有可能的分割点，算法简单、精确，当时效率低下、内存消耗大。直方图算法，不是直接扫描数据找到分割点，而是通过将连续的特征值映射到离散的槽中，使用这些离散的值构建特征，直方图算法效率更高，内存占用更少。直方图算法构建o(data * feature) ， o(bin * feature )找到对应的分割点，如果我们能够减少数据量或者需要计算的特征，算法可以得到加速。

2.2 相关工作（reduce data sample and reduce the features.）

已经有不少GBDT优雅的实现，包括XGBoost、pGBRT、sklearn、gbm in R 。sklearn和gbm通过预排序实现算法，pGBRT通过直方图实现算法。XGBoost支持预排序和直方图算法。XGBoost优于其他GBDT系列，所以使用XGBoost作为比较基准。

（reduce the size of training data）为了减少训练数据量，常规的方法是降低采样数据实例。例如，过滤掉权重值小于阈值的数据。SGB使用随机子集训练弱弱学习器，采样比率动态调整，有部分基于Adboost，不能直接应用于GBDT，因为在GBDT没有初始的权重。虽然SGB可以应用于GBDT，当时通过这种方式会损失准确度，所以这不是一个值得采用的方法。

(reduce the number of features)和采取降低数据的方法相似，自然想到的是过滤掉对于算法影响弱的特征。通常通过降维的方法，例如主成分分析或者投影法，这种降维的方法依赖假设-特征中有冗余，但是这不符合实际，每一维的特征都有其表征，取出任何特征都可能有损精度。在真实应用场景中，数据通常是稀疏的，使用预排序的GBDT通过忽略为零的特征降低训练特征。然而基于直方图的GBDT没有有效的稀疏优化方案。直方图的算法需要检索特征本值，无论特征值是否为零。基于直方图的GBDT能够有效利用如此的稀疏特性。

针对以上限制，文章提出了两种方法叫做GOSS和EFB。

3 基于梯度的one-side 采样

文章通过one-side采样在减少数据量与精确度上做很好的平衡。

3.1 算法描述

在AdaBoost中，采样权重作为数据实例重要性的衡量指标。然而在GBDT中，没有内含的样本权重，于是基于采样方法的权重不能应用于GBDT中。幸运的是，如果实例梯度值小，这个实例的误差就小，说明这个实例已经训练的很好了，直接的想法就是抛弃拥有小梯度的实例数据，这样一来数据的分布就会发生改变，会损失学到的模型的精确度。为了避免这个问题，我们提出了一种叫做GOSS的方法。GOSS保持有较大梯度的实例，在小梯度数据上运行随机采样。为了弥补这样做造成的数据分布的影响，当我们计算信息增益的时候，对于小梯度的数据GOSS引入了常量乘法器。特别的是，GOSS首先根据梯度绝对值排序，再选出a * 100%大梯度实例数据。之后在余下的数据随机采样b * 100%。经过这个过程，当计算信息增益时，GOSS使用小梯度放大了采样数据1-a/b。这样做的好处在于，我们放更多的注意力在训练实例上，而没有改变原始数据的分布。

3.2 理论分析

GBDT使用决策树学习函数，这个函数将输入变量空间映射X到梯度空间G。假设我们有独立同分布的n个实例，每个实例向量维度为空间中的S。在每次梯度Boost迭代重，关于模型输出变量的损失函数的负梯度表示为{g1 , g2 , g3}。决策树在最大信息增益的地方为分割点。对于GBDT，通常通过方差衡量分割后的信息增益。

定义3.1  O表示为决策树的固定点的训练数据集，在这个节点，分割特征 j 的方差增益定义为：

对于特征j，决策树选取 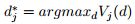使信息增益最大的特征分割。数据根据特征j*在节点dj*分割产生左右子节点。在我们提出的GOSS方法中，first:我们根据训练实例的梯度绝对值降序排列;second:选取梯度值前a * 100%的数据。然后对于剩下的训练集Ac（剩下1-a）小梯度值的实例。在剩下的实例中，随机采样大小为b * |Ac|大小的子集B。最后根据计算的方差增益分割实例为AUB 。

利用系数1-a / b 归一化梯度的和B -> A大小。

在GOSS中，我们使用在小数据集上估计的 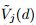，而不是在真是所有数据集上的信息增益 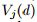，如此做计算花销将大弧度降低，下面的理论显示GOSS不会损失太多精度，比全部数据的随机采样效果更好。由于空间的限制，保留了理论证明的全过程。

根据理论，1 ， GOSS的渐进近似比例是 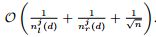，如果分割相对平衡（左侧 和右侧 ），近似误差将通过第二项减少，在数据量很大的时候，在 时间内误差降低到0，即数据量很大时，近似精确度在提高。2 ， 对于特例a = 0 时，训练集进行随机采样。在多数情况下，GOSS性能优于随机采样，细化的在条件 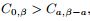同等于

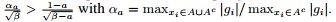
接下来，我们将分析GOSS的泛化性能。我们考虑GOSS的泛化误差为 。通过GOSS获取的是数据集上部分采样的方差增益，而不是真是的方差增益，这个地方就产生了落差。我们有公式 ，即泛化误差接近真实数据实例。采样将提高基学习器的多样性，这将提高泛化性能。

4 排他性特征绑定

通过特征绑定减少特征的数量。

高维数据通常具有稀疏的特征。稀疏的数据提供给了我们减少特征数量而较小误差损失的可能。特别是在稀疏数据中，许多特征是互斥的同时这些特征通常为非零值。我们绑定互斥的特征为单一特征（排他特征绑定）。通过仔细设计特征扫描算法，我们从特征绑定中建立相同的特征直方图作为单一特征。通过这种方式，构建直方图的复杂度从O（data * feature ） 到O（data * bundle），bundle << feature。然后我们在无损精度的情况下加速GBDT的训练。

有两个问题需要去解决：1 ， 决定什么样的特征被绑定为bundle。2 ， 怎样构建特征包。

理论4.1： 分割为互斥绑定的小数量特征是NP-hard问题。

因为图作色问题是NP-hard问题，我们将简化图作色问题到我们的问题，将NP-hard问题简化为多项式可解，我们之后会得出我们的结论。

给出图着色的实例G= （V ， E），我们将构建我们相似的实例。考虑关联矩阵G的每一行作为一个特征，我们可以获取|V|个特征。很容易获取到，我们问题中的排他绑定对应于点有相同颜色的点的集合，反之也成立。（每一行作为一个特征，相同颜色的点绑定为single特征）。理论4.1说明，在多项式时间中，找到最优绑定策略是不可行的。为了找到近似的求解算法，我们首先简化最优的绑定问题为图着色问题，定义特征为点，如果特征不互斥，则添加边到对应的点。我们使用贪心算法产生合理绑定，贪心算法能够找到找出合理图着色问题中相对合理的结果。我们也留意到有不少的特征，既不是100%互斥也同时很少取非零值。如果我们的算法能够允许小部分的冲突，我们可以得到更小度量的特征绑定和提高计算效率。通过计算，随机污染小部分的特征值会影响训练的精度到O（[（1 - γ）n ]^ -2/3）,γ是每个绑定中的最大冲突比率。所以如果我们选择相对小的γ，我们将能够完成精确度和效率之间的平衡。

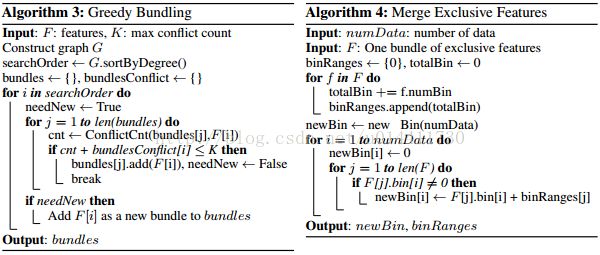
基于以上讨论，我们设计算法为排他性绑定,如算法3。

first，我们构建带权重的边，权重对应于特征之间的总体冲突。second，按照度降序排序特征。最后检查排序列表中的每个特征，这个特征应该被指派给带冲突的绑定或者创建新的绑定。算法3的时间复杂度为O(feature^2)，这个过程仅仅在训练前被处理一次。当特征的数量不是很大时。为了更进一步提高效率，我们提出了更加有效的无图构建的排序策略：按照非零值的数量排序，这个和度排序相似，因为非零值通常导致更高概率的冲突。我们仅仅改变算法3中排序的策略。

为了降低相应的训练复杂度，应该怎样合并特征到相同的包中。关键是确保原始特征值可以从特征包中区分出来。因为基于直方图的算法存储离散值而不是连续特征值，所以我们通过利用不同箱中的排他特征构建特征包。这个可以通过添加偏移指针到原始特征中。例如假定我们有两个特征在特征包中，原始特征A取值[0 , 10],特征B取值[0 , 20 ] 。我们然后添加偏移量10到特征B中，所以重新构建的特征取值为[10 , 30 ]。在这个过程后，合并A和B是安全的。使用一个新特征[0 , 30]代替原始特征 A 和B，如算法4：

EFB算法可以绑定大量的排他性特征到很少的密度特征中，这样可以有效避免零值的计算。事实上，我们可以使用表标记非零值，忽略零特征值达到优化基本的直方图算法的目的。通过扫描表中的数据，构建直方图的花销可以从O（data）到O（Non-zero-data）。这种在树构建构成中的方法需要额外的内存和计算开销维持预特征表。我们实现这个在lightGBM 作为基本的函数。顺便，这个优化和EFB不冲突，当包是稀疏的时候。

5  实验部分

这部分我们将报告lightGBM算法是实验结果，主要在五个公开数据集上做的工作。这些数据集如下说明：

微软的排序数据集LETOR包括30K网页检索查询，数据集包含的特征为密集型。Allstate保险索赔和航空延误数据集包括大量的one-hot稀疏特征。最后两个数据集来源于KDD CUP2010和KDD CUP2012.我们直接使用获胜者提取的特征，包含了稠密和稀疏的特征，这两个数据集很大。这些数据集包含了稀疏核稠密的数据，覆盖了多数真实世界的任务。

5.1 整体比较

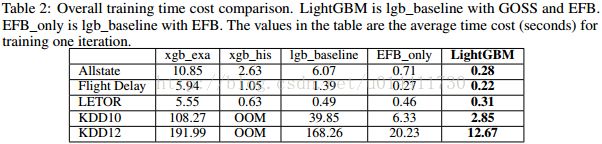
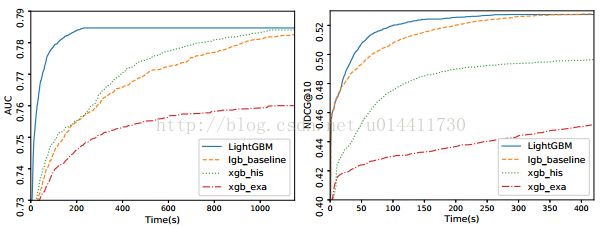
在这部分我们主要做了整体比较，XGBoost和lightGBM without GOSS 和EFB（called lgb——baseline），作为比较的基准。对于XGBoost我们使用两个版本，xgb_exa(预排序)和xgb_his(直方图算法)。对于xgb_exa，因为这仅仅支持逐层生长策略，我们调整了xgb_exa的参数，使得XGBoost长成和其他算法相似的树。我们也调整参数在速度和准确率做一个平衡。对于Allstate、KDD10 和 KDD2012,，我们设置a = 0.05 , b = 0.05 ，对于航空延误和LETOR，我们设置a = 0.1 , b = 0.1 ，数据集EFB我们设置γ = 0 。，所有的算法有固定迭代次数。在一定迭代次数内，我们取最高的分数。

表二、表三维测试时间和测试准确率。