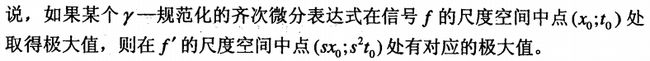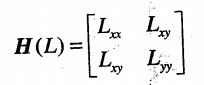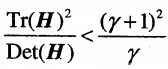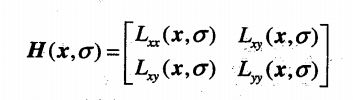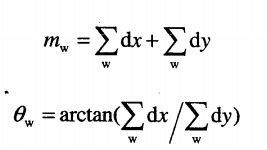图像尺度空间与Blob检测
多分辨率:
金字塔结构,采样得来,没有理论基础
多尺度:
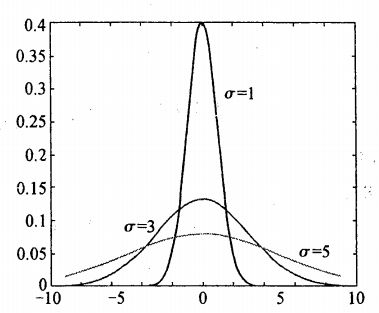
高斯核的特性:
1.孔径 blob:
2.半群性质-->叠加平滑效果:
t1,t2连续卷积相当于t1+t2的核进行卷积
3.局部极值递减:
局部极值的数量随尺度增大而递减-->平滑作用,压制小的局部细节,响应也是有减小的趋势
4.尺度不变:即使图像信号伸缩后,其尺度空间表达仍然不变
巧合:基于高斯核的尺度空间和哺乳动物的视觉认知相似。
自动尺度选择:实际上就是构建多尺度空间,找到感兴趣的尺度(物体表达的最佳尺度)
直接求最大响应是最小尺度-->不是我们希望的-->引入规范参数,消除尺度参数对响应值的影响 (怎么消除呢????)
规范后的变量为:
这样使得随着尺度的增加,响应值先增后减---->高频对应小的尺度,低频对应大的尺度
可以想象一个正弦函数,频率大,周期小,blob小,一个小尺度高斯即可覆盖
关于y值的选择的一个证明:
可以看出:

尺度不变的数学表现为:
Blob检测:
一维blob的量化:
当使用sigma=1的规范化后的高斯函数卷积时,最后一个响应值最大,假如不进行规范化,幅值会有一个sigma倍的衰减,找不到正确的极值点。
二维blob检测就是LoG,规范后之后:
卷积就是把其中一个信号(一般是短的,在卷积中称为卷积核)反褶以后的相关。
如果卷积核是对称的,卷积运算和相关运算得到的结果是一样的,比如高斯核。
所以,在这里卷积实际就是求图像与某一函数的相关性!卷积的值越大,相关性越强。
模板取自:
或者DoH(Determinant of Hessian)
带上尺度:

判决:
这里应该是sigma^2吧??
对细长的斑点有较好的抑制
模板取自:
前面:LOG,DOH,需要计算一阶、二阶微分;然后卷积(加权累加)
快速斑点检测:
引入一些简化达到斑点检测的效果。
SIFT,Lowe,1999/2004年,基于用DoG近似LoG(确切的说对σ2ΔG的近似)
SURF,Bay,2006/2008年,基于用积分图像近似DoH
(LoG优于DoH、Harris等
至此,blob=key point=intersetpoint=feature point)
SIFT
关于sift的尺度不变性和斑点检测可参考我的博文:http://blog.csdn.net/u014485485/article/details/78681086
极值点精确定位的插值:
改成矩阵形式:
写成向量形式:
注:对于n维矢量
对其求导
1.任何一个偏移量>0.5,删去
![]()
抑制边缘效应:
1.边缘的点难定位
2.易受噪声干扰
Hessian Matrix,多元函数的二阶偏导数构成的方阵,描述了函数的局部曲率。
(Hessian矩阵也是blob检测器)
SURF SpeedUp Robust Features
较SIFT算法快3倍
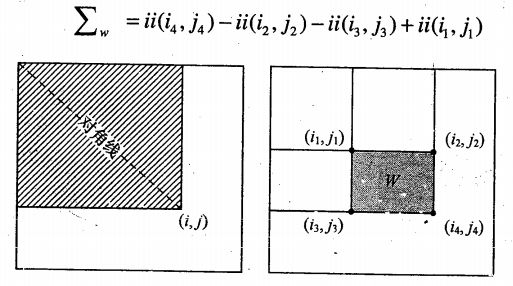
积分图像intergral image,由Viola和Jones提出,2001,将类似积分图像用于Box Filter,Simard,1999
W窗口内灰度求和:
重访DoH:
尺度为sigma的Hessian
盒子滤波Box filter用于简化计算:
设定sigma=1.2,模板9×9:
Det(H)的简化:
(注:
)
Dxx,Dyy,Dxy表示模板与图像卷积的结果。
1.模板遍历(积分图像+盒子滤波)——>某个尺度下的Hessain响应图像(注意这是一种斑点检测)
2.放大模板尺寸——>尺度空间金字塔(与SIFT不同)
3.3D非极大值抑制——>不同尺度下的斑点
模仿SIFT构建组/层:
层的构建:
(保证滤波模板有中心点)
极大值抑制时第一层和最后一层没有点被选中,结合插值,这样,最小尺寸为:
(疑问??)
组的构建:
滤波器增量翻倍6,12,24,48
第一组 9 15 21 27
第二组 15 27 39 51
第三组 27 51 75 99
第四组 51 99 147 195

组之间有重叠,目的是为了覆盖所有可能的尺度
尺度增加,斑点迅速减少
(图像可以有一个Up-scaling)
SURF对小尺度斑点较敏感
主方向:
6sigma圆形领域
统计60度扇形内x、y方向harr小波响应,然后扇形以0.2弧度大小的间隔进行旋转
采样间隔定位sigma,小波模板size定位如下图的4sigma,此时可以利用积分图加速计算
小波响应计算完之后有一个高斯加权(同SIFT)
取直方图bin值最大的以及超过最大bin值80%的那些方向作为特征点的主方向
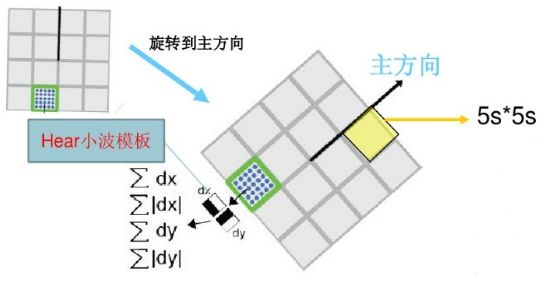
描述子:
旋转到主方向,4×4个矩形领域,每一个领域是5sigma×5sigma,统计25个像素点的harr小波响应(注:采样间隔为sigma)
(SIFT 128维)