python实现Apriori算法
★ 关联分析：
从大规模数据集中寻找物品间的隐含关系被称作关联分析。而寻找物品的不同组合是一项十分耗时的任务，所需的计算代价很高。Apriori算法正是来解决这一问题。
物品之间的关系一般可以有两种形式：频繁项集和关联规则。
频繁项集：数据集中经常出现在一块的物品的集合。
关联规则：两种物品之间可能存在很强的关系。
✿ 下面举一个大家很熟悉的 <<机器学习实战>> 上的例子:
交易代号 商品 0 豆奶、莴苣 1 莴苣、尿布、葡萄酒、甜菜 2 豆奶、尿布、葡萄酒、橙汁 3 莴苣、豆奶、尿布、葡萄酒 4 莴苣、豆奶、尿布、橙汁 我们观察这5笔交易，发现集合{葡萄酒、尿布、豆奶}就是频繁项集的其中一个例子(当然{豆奶}，{莴苣}，{豆奶、莴苣}等还有很多集合也是频繁项集)，而关联规则也可以找出，如：尿布 --> 葡萄酒，它意味着如果有人买了尿布，那么他很有可能也会买了葡萄酒。
如何度量这些关系呢？说白了就是项集怎么样才算是频繁？什么样的规则才能让我们信服？我们用支持度和可信度来度量这些有趣的关系。
项集的支持度：数据集中包含该项集的记录的比例。如{豆奶}的支持度为：
可信度： 对于关联规则{尿布} --> {葡萄酒}，它的可信度定义为：支持度({尿布，葡萄酒}) / 支持度({尿布})，即
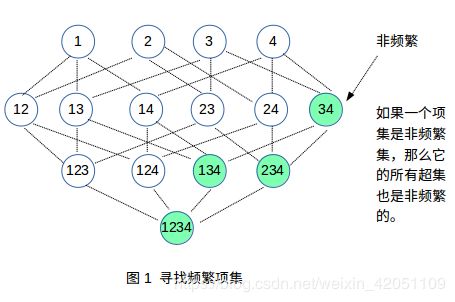
✿ 所谓的Apriori原理：
如果一个项集是非频繁集，那么它的所有超集也是非频繁的。
✿ Apriori原理的理解：
(1.) 项集的支持度可以理解为数学中的概率。而超集就是多个事件的交。
比如：豆奶的支持度为：
，而在数学的概率论中，我们可以记购买了豆奶为事件A，那么A发生的概率就是：P(A)=
，而在概率论中，A与B同时发生的概率也是：P(A•B)=
(2.) 由概率公式我们知道：P(A•B) ≤ P(A) ，通俗点讲就是：P(A的超集) ≤ P(A)，因此既然支持度就是概率，只要P(A)都不满足最小支持度要求了，那么P(A的超集) 肯定更小，它更不会满足要求，这也是我们的Apriori原理的解释。
(3.) 可信度就是条件概率。
因此，当一个项集是非频繁的，我们不需要计算它的超集了，因为它的超集不会满足我们的要求，这样就避免了项集数目的指数增长，从而在合理的时间内计算出频繁项集。
★ Apriori算法之产生频繁项集：
✿ 代码理解和疑问：
1. 产生频繁项集的流程：
(1.) Ck是候选项集列表，其中它的每个子项的大小都为k，如C1= [ {1},{2},{3}...]，C2=[ {1,2},{1,3},{2,3}...]
(2.) Lk是频繁项集列表，它是由Ck筛选出的满足最小支持度的项的集合。
首先我们创造出候选项集C1，C1是所有子项大小为1的集合列表，然后筛选出L1，再由L1自由组合创造出C2，然后把C2筛选出L2，这样一直创造筛选，直到创造出的Ck为空，那么停止。
2. loadDataSet()函数的理解：
该函数创造一个数据集，模拟商店购买记录，比如此数据集模拟了四次事务，第一次买了1、3、4号商品，第二次买了2、3、5号商品
3. createC1()函数的疑问：
该函数创造出C1，函数中对C1进行了排序，不明白它的意思。假设它是为了C1变得有序，那么接下来的scanD()函数是对C1筛选出L1，scanD()函数却没有对L1进行排序，根据原程序的意思筛选后的L1的顺序跟原始数据集dataSet有关，比如原始数据集现在是 [[1,3,4], [2,3,5], [1,2,3,5], [2,5]]，那么稍微变换每个子项的顺序[[3,1,4], [2,3,5], [1,2,3,5], [2,5]]，得到的L1顺序就不一样，那么createC1这里的排序意义在哪儿？请路过的大神解答 。
4. scanD()函数的理解与疑问：
该函数作用是从候选项集
筛选出满足最小支持度的子项从而构成频繁项集
，并且保存了每个频繁项的支持度，但是该函数返回
✿ 5. aprioriGen()函数的疑问：
该函数作用是通过频繁项集
产生候选项集Ck，因为
我的疑问是：程序中对
aprioriGen()的作用是创造出所有满足Ck的每个子项均有k个元素的所有组合，而scanD()的作用才是根据支持度筛选出符合最小支持度的频繁项集Lk，所以我对aprioriGen()函数进行了修改，使其产生所有的组合，但是这样每一层产生的候选项集Ck明显就增多了，执行效率应该会慢一些，所以我在考虑，作者用了3个sort()进行排序，又不辞辛苦使用了insert()函数，又对集合转化成列表再切片比较前k-2个元素，这么大费周章的是不是有什么数学原理可以减少Ck的项数，即：不仅scanD()函数是筛选Ck，本身产生候选项集的aprioriGen()函数也在筛选着Ck ？
我对aprioriGen()的修改是：去掉createC1()的排序 (sort的复杂度是O(n logn))
def aprioriGen(Lk, k): # 新版aproriGen lenLk = len(Lk) temp_dict = {} # 临时字典，存储 for i in range(lenLk): for j in range(i+1, lenLk): L1 = Lk[i]|Lk[j] # 两两合并，执行了 lenLk！次 if len(L1) == k: # 如果合并后的子项元素有k个，满足要求 if not L1 in temp_dict: # 把符合的新项存到字典的键中，使用字典可以去重复，比如{1,2,3}和{3，1，2}是一样的项，使用了字典就可以达到去重的作用 temp_dict[L1] = 1 return list(temp_dict) # 把字典的键转化为列表接下来是完整的创造频繁项集列表的程序：
from numpy import * def loadDataSet(): return [[1,3,4], [2,3,5], [1,2,3,5], [2,5]] def createC1(dataSet): # 创造候选项集C1，C1是大小为1的所有候选项集的集合 C1 = [] for transaction in dataSet: for item in transaction: if not [item] in C1: C1.append([item]) # C1.sort() # 从大到小排序 return list(map(frozenset,C1)) def scanD(D,Ck,minSupport): # 此函数计算支持度,筛选满足要求的项集成为频繁项集Lk，D是数据集，Ck为候选项集C1或C2或C3 ... ssCnt = {} for tid in D: for can in Ck: if can.issubset(tid): if not can in ssCnt: ssCnt[can] = 1 else: ssCnt[can] += 1 numItems = float(len(D)) retList = [] supportData = {} for key in ssCnt: support = ssCnt[key]/numItems # 计算支持度 if support >= minSupport: # 如果支持度大于设定的最小支持度 # retList.insert(0,key) retList.append(key) supportData[key] = support return retList, supportData def aprioriGen(Lk, k): # 新版aproriGen lenLk = len(Lk) temp_dict = {} # 临时字典，存储 for i in range(lenLk): for j in range(i+1, lenLk): L1 = Lk[i]|Lk[j] # 两两合并，执行了 lenLk！次 if len(L1) == k: # 如果合并后的子项元素有k个，满足要求 if not L1 in temp_dict: # 把符合的新项存到字典的键中，使用字典可以去重复，比如{1,2,3}和{3，1，2}是一样的项，使用了字典就可以达到去重的作用 temp_dict[L1] = 1 return list(temp_dict) # 把字典的键转化为列表 # def aprioriGen(Lk, k): # 根据频繁项集Lk-1创造候选项集Ck # retList = [] # lenLk = len(Lk) # for i in range(lenLk): # for j in range(i+1, lenLk): # L1 = list(Lk[i])[:k-2] # L2 = list(Lk[j])[:k-2] # L1.sort() # 排序 # L2.sort() # if L1 == L2: # 比较前Lk-1中的两个项的k-2个元素是否相同，这样才能保证合成后只有k个元素 # retList.append(Lk[i]|Lk[j]) # return retList def apriori(dataSet, minSupport = 0.5): # 通过循环得出[L1,L2,L3..]频繁项集列表 C1 = createC1(dataSet) # 创造C1 D = list(map(set,dataSet)) L1,supportData = scanD(D, C1, minSupport) 筛选出L1 L = [L1] k = 2 while (len(L[k-2]) > 0): # 创造Ck Ck = aprioriGen(L[k-2],k) Lk, supK = scanD(D,Ck,minSupport) supportData.update(supK) L.append(Lk) k += 1 return L,supportData if __name__ == "__main__": dataSet = loadDataSet() L,suppData = apriori(dataSet) print(L)★ 运行结果：
C1 [frozenset({1}), frozenset({2}), frozenset({3}), frozenset({4}), frozenset({5})]
L1 [frozenset({1}), frozenset({3}), frozenset({2}), frozenset({5})]
生成的候选项集 [frozenset({1, 3}), frozenset({1, 2}), frozenset({1, 5}), frozenset({2, 3}), frozenset({3, 5}), frozenset({2, 5})]
筛选出频繁项集 [frozenset({1, 3}), frozenset({2, 3}), frozenset({3, 5}), frozenset({2, 5})]
生成的候选项集 [frozenset({1, 2, 3}), frozenset({1, 3, 5}), frozenset({2, 3, 5})]
筛选出频繁项集 [frozenset({2, 3, 5})]
生成的候选项集 []
筛选出频繁项集 []
★ Apriori算法之挖掘关联规则：
我们挖掘物品之间的关系，是需要同时满足两个度量的：一个是要满足支持度，二是要满足可信度。因此我们在挖掘关联规则时只需要在频繁项集上挖掘就可以了，因为只有频繁项集才满足最小支持度。在频繁项集上创建所有规则之后，再筛选出满足可信度的规则就算大功告成了，即使如此，一个频繁项集的一个子项所能创造出来的规则，也非常多，计算量也很大，比如L3的一个子项{2,3,5}，产生的规则有: {2,3} --> {5}，{2,5} --> {3}，{3,5} --> {2}，{2} --> {3,5}，{3} --> {2,5}，{5} --> {2,3}，由此看到数量也不少，我们需要用Apriori原理进行优化。
✿ 前文我们提到，支持度就是概率，可信度就是条件概率。
假如某一规则为： A --> B，A叫做左件，B叫做右件。它的意思是有人已经买了商品A，那么他还会买商品B的概率较大。这正好对应数学中的条件概率 P(B｜A) ，根据定义，该规则的可信度= 支持度{A、B} / 支持度{A}，正好与条件概率公式相符，因此：
可信度= P(B｜A) = P(B•A) / P(A) ①
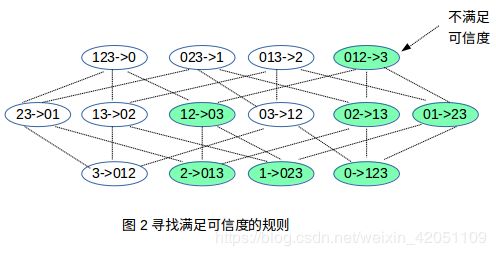
举个例子，对于一个频繁项集的子项{0123}，它可以产生的规则如图：
✿ 我们根据公式①看出Apriori原理：(跟书上不同哦)
(1.) 对于右件B，假如它不满足最低可信度，那么它的超集做右件也一定不满足可信度。
由概率公式：P(B) ≥ P(B的超集)，因此 P(B•A) ≥ P(B的超集•A)。所以，假如P(B•A)都不满足可信度要求，那么P(B的超集•A)做分子，更不符合要求。
★ Apriori算法之挖掘关联规则的代码流程：
✿ 流程：
我们先得到每层的频繁项集Lk，然后一层一层的创建关联规则，当然需要 k≥2，假如 k =1，L1= [ {1},{2}...]这怎么创建，1--> Ø，2-->Ø 吗？所以创造规则时忽略 L1，直接从L2开始。
当k=2的时候，我们没法用Apriori原理预先减去多余的项，如：L2= [ {1,2},{1,3}...]，创造出的规则是1-->2，1-->3...，然后通过计算每条规则的可信度来筛选符合要求的规则。
当 k > 2 时，这时可以用Apriori原理预先减去多余的项了，比如此时k =4，拿出L4的一个频繁项 frozenset({0,1,2,3})，如上图2，假如右件{3}不满足最小可信度要求，根据Apriori原理，那么{3}的超集作为右件的所有规则也不满足最小可信度要求，那么我们就无需计算它的超集了，这就减少了计算量。而如何实现呢？我们只要把不符合可信度条件的右件存起来，然后把他们拆分成单个元素并去重，把可组合的元素集合减去刚才拆分出来的不满足可信度的元素集合，剩下的就是下一轮可组合的集合，然后两两或三三或四四自由组合出新右件，这样的新右件肯定不是刚才那个不满足可信度的右件的超集，因为新右件组合的时候，就没用到那个不满足可信度的右件(因为我们刚才把不满足的右件元素减去了)，组合出来后肯定不是它的超集，这就应用了Apriori原理。
具体实现是：
我们就以上图2为例：
频繁项为[frozenset({0,1,2,3})]，我们把它拆分成单个元素组成的列表 H = [frozenset({0})，frozenset({1})，frozenset({2})，frozenset({3})]，这个H就是待组合成右件的元素集合列表，比如它可以两两
组合，也可以三三组合。我们用H1表示H自由组合后的右件，根据Apriori原理，我们先把H组合成右件只有一个元素的列表(也就是先创建图2的第一层规则)，既然右件只有一个元素，那么H1正好等于H，把H1做右件，进行calcConf()筛选满足可信度的规则，假如{3}做右件不满足可信度要求，那么把{3}存到一个列表prunedH中，成为了[frozenset({3)]，然后我们在待组合元素列表H减去这个不满足的右件元素{3}，不就相当于把这个不满足可信度的右件元素删除了，此时H=[frozenset({0})，frozenset({1})，frozenset({2})]，那么接下来的H再两两组合，得到的右件列表肯定不是刚才那个不满足可信度的右件元素的超集，因为刚才把它删除了，再组合肯定没有这个元素出现了，这就是Apriori原理的使用，如此这么循环下去，H这么一直减元素，当H里的元素个数小于需要的右件元素个数时，就停止，比如，H还剩下两个元素了，H=[frozenset({1}),frozenset({2})]，而接下来右件元素数需要3个，那么显然它组合不出这样的右件，也就停止了。还有一种停止条件是：当右件元素的个数 = len(原频繁项)的时候，停止，因为根据频繁项创建规则，右件元素的个数最多是len(原频繁项)-1 。
✿ 具体代码：
✿ 代码理解与疑问：
(1.) calcConf()改动：
该函数作用是计算符合可信度要求的规则，并把不符合可信度要求的右件存到一个列表中，函数中的conseq是右件，freqSet是原始频繁项，freqSet-conseq是左件。
✿ (2.) rulesFromConseq()函数的疑问：
该函数是Lk(k>2)频繁项集上创造规则，并应用Apriori原理减少创造的规则，再交给calcConf()去再次筛选。书上源码没看懂，我给出了自己的代码。
拿过一个频繁项，先把该频繁项拆开，如frozenset({2,3,5})，拆了后就是 H=[frozenset({2}),frozenset({3}),frozenset({5})]，这个H就是待组合的元素列表，它可以两两组合，三三组合...，H1是H自由组合后的右件列表，第一次循环右件只有一个元素，因此H1就是H，然后H1的每一项分别做右件。不满足要求的右件的组合保存在一个列表中，待会下次循环我们会把这个不满足可信度的右件的所有组成元素从H中都删去，那么下次H再自由组成H1的时候就不会出现刚才不满足可信度的右件的超集，比如：右件{3}不满足可信度，那么我们把它存到列表中[frozenset({3})]，让H减去这个集合后，H=[frozenset({2}),frozenset({5})]，此时H再自由组合成H1，就是H1=[frozenset({2,5})]，显然没有{3}的超集，这就应用了Apriori原理。随着循环的进行，H就这样一直减不符合可信度的右件的所有组成元素，知道H里面的元素太少，组成不了符合要求的右件了，停止，还有一个停止条件是：当右件元素的个数 = len(原频繁项)的时候，停止，因为根据频繁项创建规则，右件元素的个数最多是len(原频繁项)-1 。
(3.) generateRules()函数的理解
该函数作用是产生规则，分为两种情况：一种是可用Apriori原理来减少 Lk(k>2) 频繁项创造出的规则，第二种是不能用Apriori原理去减少 L2 频繁项产生的规则。
def calcConf(freqSet, H, supportData, br1, minConf = 0.7): # 筛选符合可信度要求的规则，并返回符合可信度要求的右件 prunedH = [] # 存储符合可信度的右件 for conseq in H: # conseq就是右件，freqSet是原始频繁项,freqSet-conseq是左件 conf = supportData[freqSet]/supportData[freqSet-conseq] # 计算可信度 if conf>= minConf: print(freqSet-conseq,"-->",conseq,"\tconf:",conf) br1.append((freqSet-conseq,conseq,conf)) else: prunedH.append(conseq) # 不符合可信度的右件添加到列表中 return prunedH # def rulesFromConseq(freqSet, H, supportData, br1, minConf=0.7): # 原版Apriori原理来减少创造的规则 # m = len(H[0]) # if (len(freqSet)>(m+1)): # Hmp1 = aprioriGen(H, m+1) # Hmp1 = calcConf(freqSet, Hmp1, supportData, br1, minConf) # if (len(Hmp1) >1): # rulesFromConseq(freqSet, Hmp1, supportData, br1,minConf) def rulesFromConseq(freqSet, H, supportData, br1, minConf=0.7): # 新版Apriori原理来减少创造的规则 is_find = True # 循环标志 m = 1 # 先创造右件为一个元素的规则 Hmp1 = H # H是初始频繁项分散后的列表，[frozenset({2}),frozenset({3}),frozenset({5)],Hmp1是组合后的右件，因为我们的aprioriGen不能组建只有1个元素的右件，所以右件为1个元素的时候我们直接H赋值过去，当右件元素数是2以上的时候，再用aprioriGen组合出来 while is_find: if len(freqSet) > m: # 最多循环len(freqSet)-1次，因为右件最多len(freqSet)-1个元素，右件元素的数从1增长到len(freqSet)-1，故最多循环len(freqSet)-1次 if m > 1: # 我们改编的aprioriGen()函数至少产生C2,不能产生C1，因此这里加了if Hmp1 = aprioriGen(H,m) # H里的元素自由组合成右件，右件的元素个数是m H_no = calcConf(freqSet, Hmp1, supportData, br1, minConf) # 筛选符合可信度的规则,把不符合的右件存起来 if len(H_no) != 0: # 如果有不满足可信度的右件 H_no = list(set(frozenset([item]) for row in Hmp1 for item in row)) # 我们把列表中的每个元素都分割出来，比如[{2,3},{3,4}] 分割后为[{2},{3},{4}]，方便我们再次组合，这里也是Apriori原理的精髓所在，这么操作就是把不满足的右件及其超集提出来，然后后面做减法。 H = list(set(H)-set(H_no)) # 可组合的集合减去不满足可信度的右件的集合 m = m + 1 # 右件个数不断增加，第一次右件元素只有1个，第二次循环右件元素就有两个了 if len(H) < m: # 如果剩余的可自由组合的元素个数少于新右件所需要的元素数，比如就剩两个元素可组合了，想要组成C3作右件，肯定是不可能的，那么结束循环 is_find = False else: # 如果循环次数达到最大，也结束循环 is_find = False def generateRules(L, supportData, minConf=0.7): # 产生规则 bigRuleList = [] for i in range(1, len(L)): # 从L2开始创造规则 for freqSet in L[i]: H1 = [frozenset([item]) for item in freqSet] if i>1: # L3开始使用Apriori原理 rulesFromConseq(freqSet, H1, supportData, bigRuleList, minConf) else: # L2不能使用Apriori原理，只能老老实实挨个创造规则 calcConf(freqSet, H1, supportData, bigRuleList, minConf) return bigRuleList
★ 完整代码及结果：
from numpy import * import time def loadDataSet(): return [[1,3,4], [2,3,5], [1,2,3,5], [2,5]] def createC1(dataSet): C1 = [] for transaction in dataSet: for item in transaction: if not [item] in C1: C1.append([item]) C1.sort() return list(map(frozenset,C1)) def scanD(D,Ck,minSupport): ssCnt = {} for tid in D: for can in Ck: if can.issubset(tid): if not can in ssCnt: ssCnt[can] = 1 else: ssCnt[can] += 1 numItems = float(len(D)) retList = [] supportData = {} for key in ssCnt: support = ssCnt[key]/numItems if support >= minSupport: # retList.insert(0,key) retList.append(key) supportData[key] = support return retList, supportData # def aprioriGen(Lk, k): # retList = [] # lenLk = len(Lk) # for i in range(lenLk): # for j in range(i+1, lenLk): # L1 = list(Lk[i])[:k-2] # L2 = list(Lk[j])[:k-2] # L1.sort() # L2.sort() # if L1 == L2: # retList.append(Lk[i]|Lk[j]) # return retList def aprioriGen(Lk, k): lenLk = len(Lk) temp_dict = {} for i in range(lenLk): for j in range(i+1, lenLk): L1 = Lk[i]|Lk[j] if len(L1) == k: if not L1 in temp_dict: temp_dict[L1] = 1 return list(temp_dict) def apriori(dataSet, minSupport = 0.5): C1 = createC1(dataSet) # print("C1",C1) D = list(map(set,dataSet)) L1,supportData = scanD(D, C1, minSupport) # print("L1",L1) L = [L1] k = 2 while (len(L[k-2]) > 0): Ck = aprioriGen(L[k-2],k) # 生成候选项集 # print("生成的候选项集",Ck) Lk, supK = scanD(D,Ck,minSupport) # 按支持度筛选候选项集 # print("筛选出频繁项集",Lk) supportData.update(supK) L.append(Lk) k += 1 return L,supportData def calcConf(freqSet, H, supportData, br1, minConf = 0.7): # 筛选符合可信度要求的规则，并返回符合可信度要求的右件 prunedH = [] # 存储符合可信度的右件 for conseq in H: # conseq就是右件，freqSet是原始频繁项,freqSet-conseq是左件 conf = supportData[freqSet]/supportData[freqSet-conseq] # 计算可信度 if conf>= minConf: print(freqSet-conseq,"-->",conseq,"\tconf:",conf) br1.append((freqSet-conseq,conseq,conf)) else: prunedH.append(conseq) # 不符合可信度的右件添加到列表中 return prunedH # def rulesFromConseq(freqSet, H, supportData, br1, minConf=0.7): # 原版Apriori原理来减少创造的规则 # m = len(H[0]) # if (len(freqSet)>(m+1)): # Hmp1 = aprioriGen(H, m+1) # Hmp1 = calcConf(freqSet, Hmp1, supportData, br1, minConf) # if (len(Hmp1) >1): # rulesFromConseq(freqSet, Hmp1, supportData, br1,minConf) def rulesFromConseq(freqSet, H, supportData, br1, minConf=0.7): # 新版Apriori原理来减少创造的规则 is_find = True # 循环标志 m = 1 # 先创造右件为一个元素的规则 Hmp1 = H # H是初始频繁项分散后的列表，[frozenset({2}),frozenset({3}),frozenset({5)],Hmp1是组合后的右件，因为我们的aprioriGen不能组建只有1个元素的右件，所以右件为1个元素的时候我们直接H赋值过去，当右件元素数是2以上的时候，再用aprioriGen组合出来 while is_find: if len(freqSet) > m: # 最多循环len(freqSet)-1次，因为右件最多len(freqSet)-1个元素，右件元素的数从1增长到len(freqSet)-1，故最多循环len(freqSet)-1次 if m > 1: # 我们改编的aprioriGen()函数至少产生C2,不能产生C1，因此这里加了if Hmp1 = aprioriGen(H,m) # H里的元素自由组合成右件，右件的元素个数是m H_no = calcConf(freqSet, Hmp1, supportData, br1, minConf) # 筛选符合可信度的规则,把不符合的右件存起来 if len(H_no) != 0: # 如果有不满足可信度的右件 H_no = list(set(frozenset([item]) for row in Hmp1 for item in row)) # 我们把列表中的每个元素都分割出来，比如[{2,3},{3,4}] 分割后为[{2},{3},{4}]，方便我们再次组合，这里也是Apriori原理的精髓所在，这么操作就是把不满足的右件及其超集提出来，然后后面做减法。 H = list(set(H)-set(H_no)) # 可组合的集合减去不满足可信度的右件的集合 m = m + 1 # 右件个数不断增加，第一次右件元素只有1个，第二次循环右件元素就有两个了 if len(H) < m: # 如果剩余的可自由组合的元素个数少于新右件所需要的元素数，比如就剩两个元素可组合了，想要组成C3作右件，肯定是不可能的，那么结束循环 is_find = False else: # 如果循环次数达到最大，也结束循环 is_find = False def generateRules(L, supportData, minConf=0.7): # 产生规则 bigRuleList = [] for i in range(1, len(L)): # 从L2开始创造规则 for freqSet in L[i]: H1 = [frozenset([item]) for item in freqSet] if i>1: # L3开始使用Apriori原理 rulesFromConseq(freqSet, H1, supportData, bigRuleList, minConf) else: # L2不能使用Apriori原理，只能老老实实挨个创造规则 calcConf(freqSet, H1, supportData, bigRuleList, minConf) return bigRuleList if __name__ == "__main__": dataSet = loadDataSet() begin_time = time.time() L,suppData = apriori(dataSet) rules = generateRules(L, suppData, minConf=0.5) end_time = time.time() print("程序花费时间{}秒".format(end_time-begin_time)) # print(L) # print(suppData)✿ 运行结果：
frozenset({3}) --> frozenset({1}) conf: 0.6666666666666666
frozenset({1}) --> frozenset({3}) conf: 1.0
frozenset({3}) --> frozenset({2}) conf: 0.6666666666666666
frozenset({2}) --> frozenset({3}) conf: 0.6666666666666666
frozenset({5}) --> frozenset({3}) conf: 0.6666666666666666
frozenset({3}) --> frozenset({5}) conf: 0.6666666666666666
frozenset({5}) --> frozenset({2}) conf: 1.0
frozenset({2}) --> frozenset({5}) conf: 1.0
frozenset({3, 5}) --> frozenset({2}) conf: 1.0
frozenset({2, 5}) --> frozenset({3}) conf: 0.6666666666666666
frozenset({2, 3}) --> frozenset({5}) conf: 1.0
frozenset({5}) --> frozenset({2, 3}) conf: 0.6666666666666666
frozenset({2}) --> frozenset({3, 5}) conf: 0.6666666666666666
frozenset({3}) --> frozenset({2, 5}) conf: 0.6666666666666666
程序花费时间0.001077890396118164秒