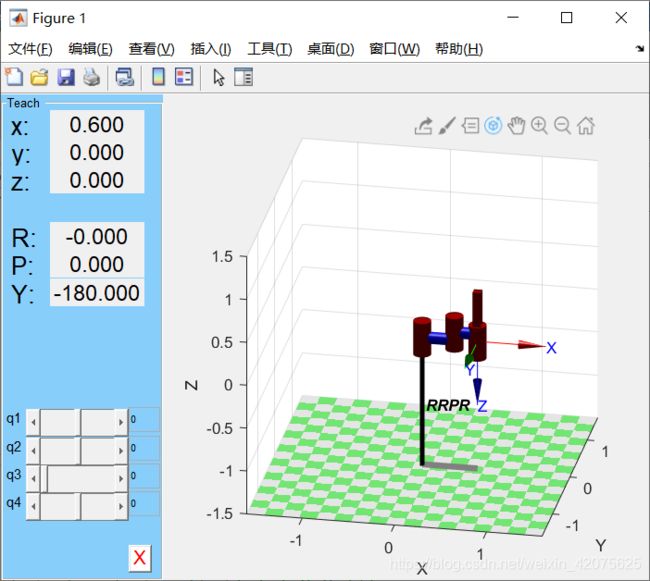
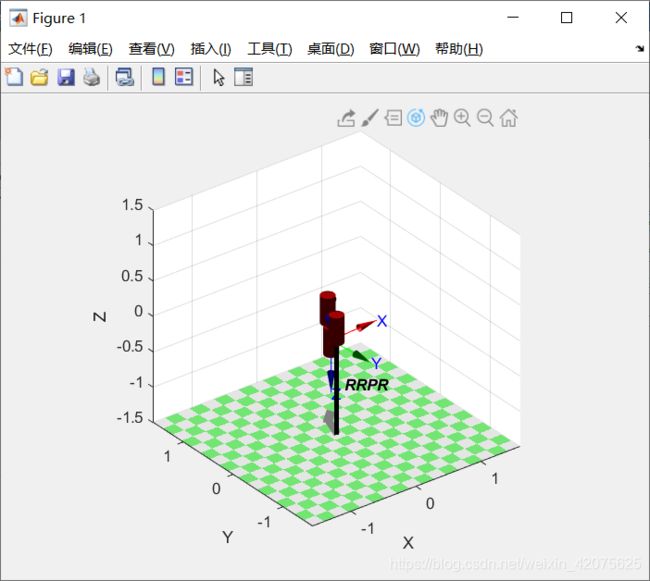
rrpr机器臂的matalb Robotic Toolbox工具箱的使用

工具箱版本10.3.1

使用改进ＤＨ法建立连杆坐标系,连杆数据可以改变,文中代码是直接从matlab编辑器里copy过来的,可以忽略那些数据.对机器人工具箱使用不熟的同学推荐

https://blog.csdn.net/qq_35551200/article/details/97030782

先上结果

上代码

%theta d a alpha
L(1)=Link([0 0 0 0 0],'modified');
L(1).qlim=[-pi,pi];

L(2)=Link([0 0.0855 0.35 0 0],'modified');
L(2).qlim=[-pi,pi];

L(3)=Link([0 0 0.25 -pi 1],'modified');
L(3).qlim=[0,1];

L(4)=Link([0 0.0855 0 0 0],'modified');
L(4).qlim=[-pi,pi];

robot=SerialLink(L,'name','RRPR');
robot.plot([0 0 0 0],'workspace',[-1.5 1.5  -1.5 1.5 -1.5 1.5]);
robot.teach([0 0 0 0]);

使用robot.teach()方便手动改变各个关节的角度

设置qlim函数设置关节运动范围,workspace属性设置工作空间的大小.到此完成简单建模.

下面是正运动学和逆运动学部分

上代码

p=robot.fkine([60 -30 0.5 30],'deg');
ip=robot.ikine(p,'mask',[1 1 1 0 0 1]);
 %'mask',mask是一个6*1的向量，分别代表XYZ的移动和XYZ的转动自由度

运行结果为

ip为弧度制,与fkine函数中设置的值对比,可以发现是一致的.

此处注意ikine函数中的'mask'属性,在matlab命令行输入help robot.ikine,查看帮助

mask矩阵前三个相当于笛卡尔坐标值,后三个相当于姿态角.因为我们的机械臂最后的转动关节只绕Z轴旋转,所以设置mask为

[1 1 1 0 0 1]. 但也有问题,我们通过命令p=robot.fkine([60 -30 0.5 30],'deg')获取变换矩阵,通过ip=robot.ikine(p,'mask',[1 1 1 0 0 1])命令求解某变换矩阵对应的关节角,实际发现当关节角运动值变大时,假如设置[60 -80 0.5 60],求解出的关节角可能会存在问题,目前尚未解决.大佬们知道原因的话请评论告知,十分感谢.

       最后,技术不够努力来凑,这种类型机械臂用代数解法求逆运动学公式还是可以的,具体参照<<机器人学导论>>第四版81页82页,解法类似.

到此,我们完成建模,同时也完成了正运动学和逆运动学,下面是轨迹规划.

上代码

  T1=SE3([0.1 0.2 0])*SE3.Rz(pi/4);%根据给定起始点，得到起始点位姿
  T2=SE3([0.3,0.5,-0.5])*SE3.Rz(pi/2)%根据给定终止点，得到终止点位姿
  q1=robot.ikine(T1,'mask',[1 1 1 0 0 1]);%根据起始点位姿，得到起始点关节角
  q2=robot.ikine(T2,'mask',[1 1 1 0 0 1]);%根据终止点位姿，得到终止点关节角
  
  t=[0:0.05:2]';
  [q,qd,qdd]=jtraj(q1,q2,t);
 
  T=robot.fkine(q);
  robot.plot(q);%动画演示

jtraj函数不懂得可以在命令行help jtraj 

      其实轨迹规划的函数比较容易,大家可以在命令行open jtraj或者open lspb 或者open tpoly看看源文件,学习一下大佬的代码,还是能看明白的,(笔者这种菜鸟看了好久才明白)

然后我们加两行代码观察关节1的位置变化

  figure
  plot(t,q(:,1));

和前面逆运动学求解的起始位置和终止位置符合.

最后我们看动画演示