Self-attention计算方法
三个矩阵
首先,Inputs为x1~x4,是一个sequence,每一个Input先通过一个Embedding,乘上一个Matrix得到(a1,a4),然后放入self-attention
在self-attention当中,每一个Input都分别乘上3个不同的Matrix产生3个不同的Vector,分别命名为q,k,v

q代表query,to match others,每一个Input都乘上一个Matrix Wq,就得到q1~q4,叫做query
k代表key,to be matched计算同上
v就是要被抽取出来的information,计算同上

现在,每一个a都有qkv3个不同的Vector,接下来,拿每一个query q,去对每一个key k去做attention
attention简单来说就是输入2个向量,out一个分数 先看q1,对k1做attention,得到α1,1
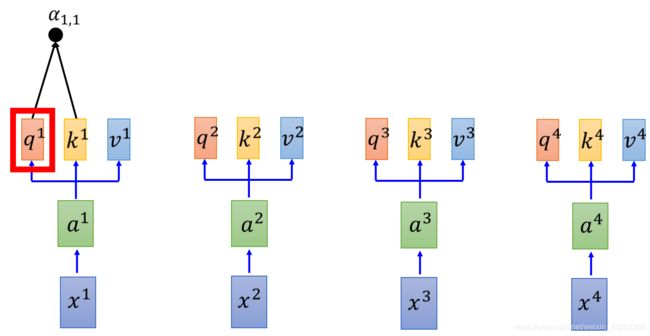
同理得到α1,2,α1,3,α1,4,至此得到了q1对k1,2,3,4的attention,d为q与k的Dimension(维度),因为q与k做点乘,所以维度越大,算出来的值越大。
前面说过attention是输入2个Vector,输出1个out分值,不能让分值随向量维度的增大而增大,softmax之后会导致梯度消失,所以要先进行一个缩放。
也可以尝试用其他的attention,不一定要用Dot-Product Attention

接下来将得到的α1,1~α1,4通过一个softmax层得到 α ^ \hat α α^
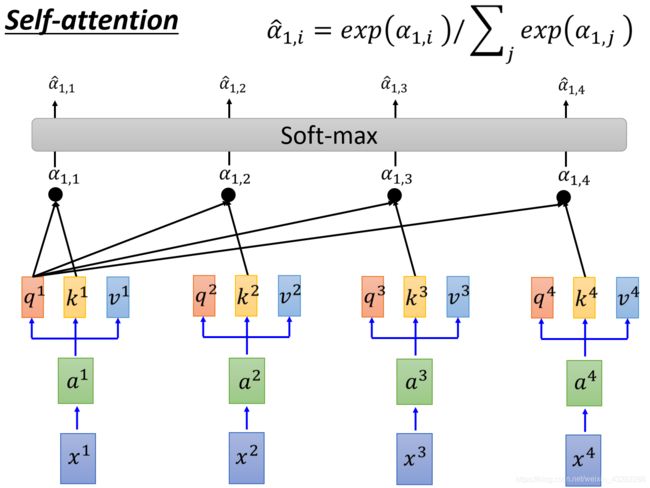
然后拿 α ^ \hat α α^去和每一个v相乘,得到的Vector加起来,就得到了一个Vector,这个Vector就是b1
self-attention输入是一个sequence,输出也是一个sequence,现在得到了输出的seq的第一个Vector b1,此时可以知道,产生b1的时候,已经看到了a1~a4的词序
如果产生b1的时候不想考虑整个句子的词序,只想考虑local的information,只需要让 α ^ \hat α α^234产生出来的值变为0,就可以只考虑local的information
而如果要考虑最远的x4产生的影响,只需要让 α ^ \hat α α^4有值就可以了

刚刚算出来了b1,在同时也可以算b2,b3,b4

现在得到b1~b4,且他们可以平行的被计算出来,可以被加速。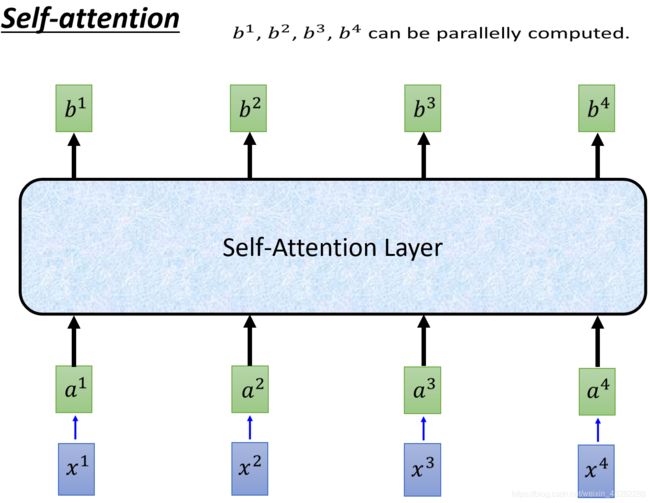
平行化
那么self-attention是怎么做平行化的?
刚刚讲
a1乘上一个Wq得到q1
a2乘上一个Wq得到q2
所以可以把a1到a4拼起来变成一个Matrix,用I表示,用I乘上Wq就可以得到Q,Q中每一个col(q)代表一个query



刚刚讲到,用q1,对每一个做attention,其实就是做Dot-Product,省略了 d \sqrt d d更简洁一点,这里将k1转置,得到α1,1 ,同理得到α1,2,α1,3,α1,4,其实都是q1与不同的k做Dot-Product,所以可以将所有的k集合在一起,将所有的k当做一个Matrix 的row(行),这个Matrix 乘上q1得到的结果就是一个向量即α1,1~α1,4
所以 α 1 , 1 α_{1,1} α1,1~ α 1 , 4 α_{1,4} α1,4的计算是可以平行的

q 2 q_2 q2也是一样的
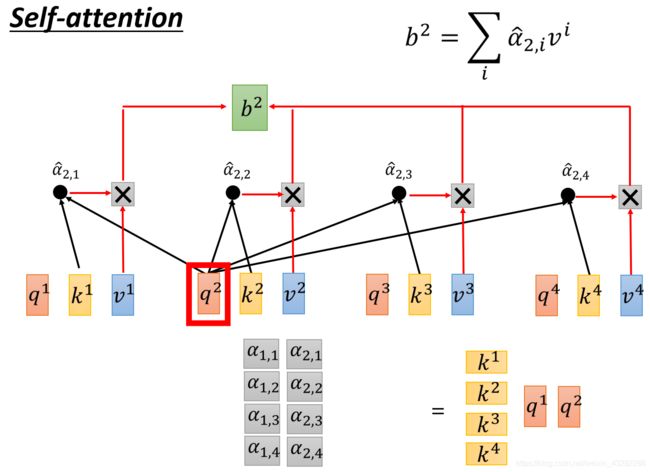
同理可得 q 3 q_3 q3, q 4 q_4 q4

所以计算出整个attention的过程,就等于是我们得到的K做一个转置直接乘上Q就得到attention A,Input为4,A为4x4,如果Input为N,则A为NxN,接下来做softmax得到 A ^ \hat A A^

b的计算同上

V和 A ^ \hat A A^相乘就得到了O

整体流程Attention(Q,K,V)=softmax( Q K T d k {QK^T\over \sqrt {d_k}} dkQKT)V
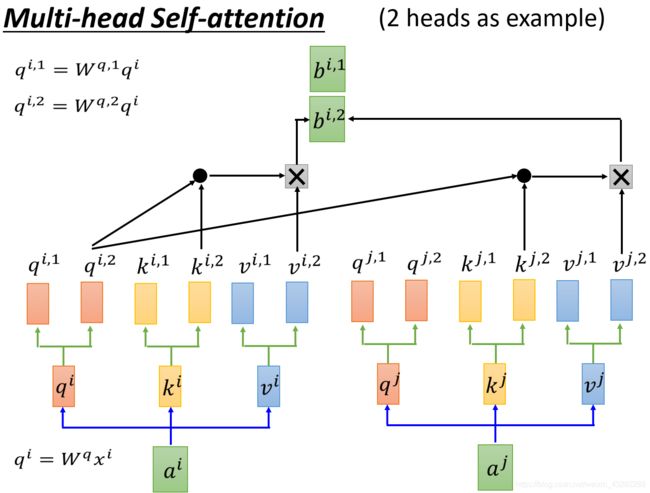
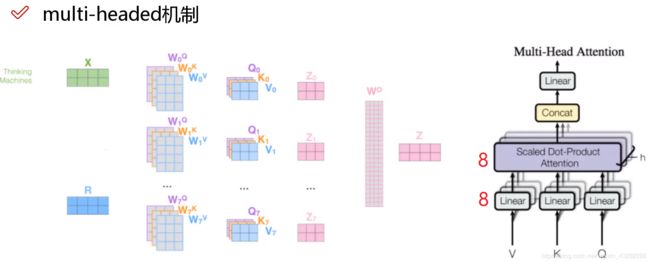
Multi-headed
作用,如同卷积网络中的多个filter一样

原文给出的是8个head

举例2个head的计算方法:
要做 q i , 1 q^{i,1} qi,1与别的词做attention,要先与 k i , 1 k^{i,1} ki,1 k j , 1 k^{j,1} kj,1做Dot-Product最后计算出 b i , 1 b^{i,1} bi,1
q i , 2 q^{i,2} qi,2也是一样,最后得到 b i , 2 b^{i,2} bi,2