Self-Attention与Transformer
1.由来
在Transformer之前,做翻译的时候,一般用基于RNN的Encoder-Decoder模型。从X翻译到Y。
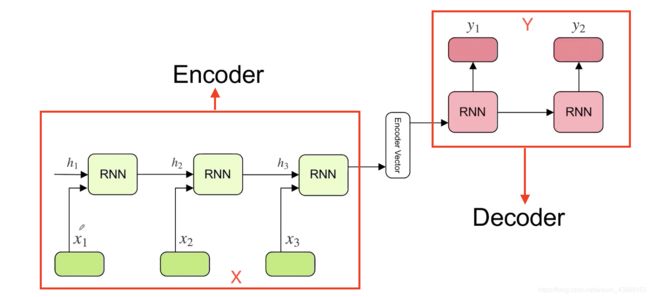
但是这种方式是基于RNN模型,存在两个问题。
一是RNN存在梯度消失的问题。(LSTM/GRU只是缓解这个问题)
二是RNN 有时间上的方向性,不能用于并行操作。Transformer 摆脱了RNN这种问题。
2.Transformer 的整体框架
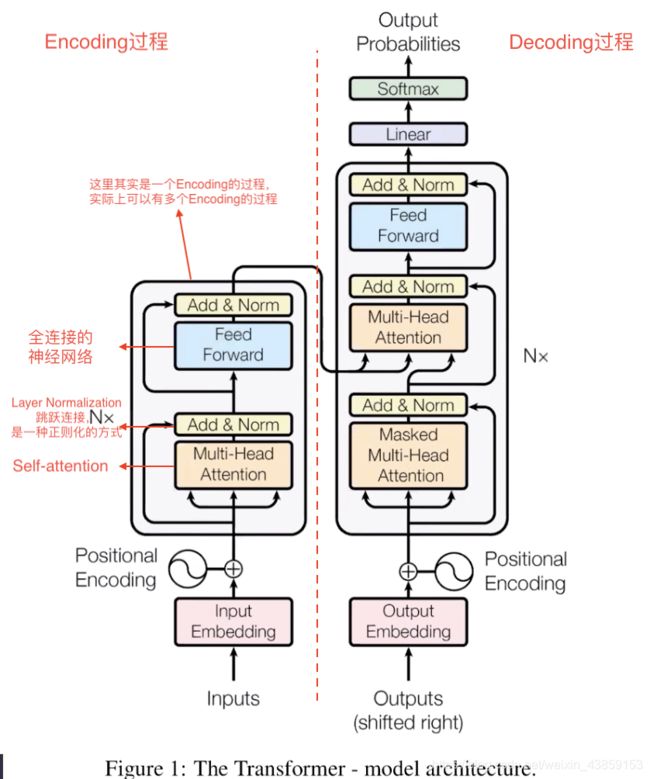


输入的 x 1 , x 2 x_{1},x_{2} x1,x2,共同经过Self-attention机制后,在Self-attention中实现了信息的交互,分别得到了 z 1 , z 2 z_{1},z_{2} z1,z2,将 z 1 , z 2 z_{1},z_{2} z1,z2分别经过各自的全连接神经网络之后,得到了 r 1 , r 2 r_{1},r_{2} r1,r2。
self-attention的意义是
当使用Transformer模型翻译’’ The animal didn’t cross the street because it was too tired"。当翻译到it时, 我们知道 it 指代的是 animal 而不是street. 所以, 如果有办法可以让 it 对应位置的embedding 适当包含 animal 的信息,就会非常有用. self-attention的出现就是为了完成这一任务.
如上图右侧所示,self-attention会让单词it和某些单词发生比较强的联系, 得到比较高的attention分数.
3.Self-attention机制
3.1Self-attention解释

假设 x 1 , x 2 ∈ R 1 × 4 x_{1},x_{2}\in R^{1 \times 4} x1,x2∈R1×4,
同时引入三个矩阵,Queries矩阵: W Q ∈ R 4 × 3 W^{Q}\in R^{4 \times 3} WQ∈R4×3,Key矩阵: W K ∈ R 4 × 3 W^{K}\in R^{4 \times 3} WK∈R4×3,Values矩阵: W V ∈ R 4 × 3 W^{V}\in R^{4 \times 3} WV∈R4×3。
将 x 1 x_{1} x1与 W Q W^{Q} WQ, W K W^{K} WK, W V W^{V} WV分别作矩阵乘法,分别得到 q 1 , k 1 , v 1 ∈ R 1 × 3 q_{1},k_{1},v_{1}\in R^{1 \times 3} q1,k1,v1∈R1×3,同理可得到 q 2 , k 2 , v 2 ∈ R 1 × 3 q_{2},k_{2},v_{2}\in R^{1 \times 3} q2,k2,v2∈R1×3。
之后来到上图的右半部分,
将 q 1 , k 1 q_{1},k_{1} q1,k1中的对应位置元素相乘再求和(点积的方式)得到 q 1 ⋅ k 1 = 112 q_{1}\cdot k_{1}=112 q1⋅k1=112,将 112 8 = 14 \displaystyle\frac{112}{8}=14 8112=14,在经过Softmax之后得到0.88,
同理,将 q 1 , k 2 q_{1},k_{2} q1,k2点积相乘得到 q 1 ⋅ k 2 = 96 q_{1}\cdot k_{2}=96 q1⋅k2=96,将 96 8 = 12 \displaystyle\frac{96}{8}=12 896=12,在经过Softmax之后得到0.12,
最后将 0.88 v 1 + 0.12 v 2 = z 1 0.88 v_{1}+0.12v_{2}=z_{1} 0.88v1+0.12v2=z1。同样的,可以得到 z 2 z_{2} z2。
3.2Self-attention矩阵表示

表示称矩阵形式为
X = ( x 1 x 2 ) ∈ R 2 × 4 X=\left(\begin{array}{ll}{x_{1}} \\ {x_{2}} \end{array}\right) \in R^{2\times4} X=(x1x2)∈R2×4,分别与 W Q W^{Q} WQ, W K W^{K} WK, W V W^{V} WV作矩阵乘法,分别得到 Q , K , V ∈ R 2 × 3 Q,K,V\in R^{2 \times 3} Q,K,V∈R2×3, Z = S o f t m a x ( Q × K T 8 ) V Z=Softmax(\displaystyle\frac{Q \times K^{T}}{8})V Z=Softmax(8Q×KT)V。
如果有8个 W Q W^{Q} WQ, W K W^{K} WK, W V W^{V} WV,就会得到8个的 Z i Z_{i} Zi(类似卷积神经网络),那么这8个 Z i Z_{i} Zi又该如何组合呢?

这里的话使用了一个全连接的神经网络来组合,将8个 Z i Z_{i} Zi拼接成 R 24 × 2 R^{24\times 2} R24×2,经过一个全连接的神经网络,最终得到 Z Z Z。
Multi-headed Self-Attention整体结构

观察一下结果,下图右是整体的结果,下图左是其中2个attention的结果,以下图左举例,橙色的attention注意力机制“注意到”it与The animal这个关联性较强,而绿色的attention注意力机制“注意到”it与tired关联性较强,这也是设计多个header的原因。

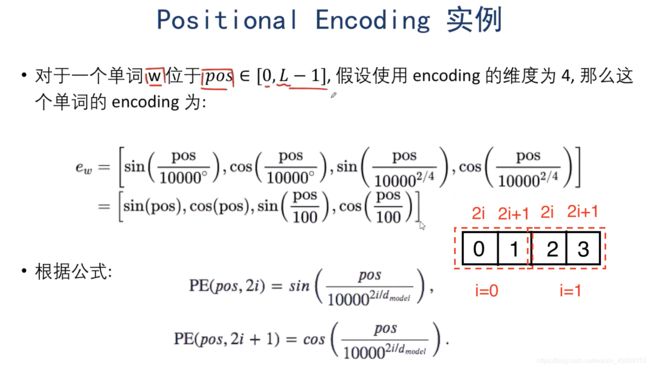
4.Positional Encoding
对于输入的 X X X,不仅需要将单词转化成词向量的形式,而且需要加入每个单词的位置的信息,如图所示,输入的 x 1 = x_{1}= x1=词向量+词的位置信息


d m o d e l d_{model} dmodel为词向量的维度,下图是例子
5.Layer Normalization
使用Layer Normalization的原因是当网络比较深的时候,使用梯度下降法向后传递误差时,误差项会越来越弱,训练起来就会比较慢,比较困难


因此在self-attention之后,加入Layer Normalization ( X + Z ) (X+Z) (X+Z),得到新的 Z Z Z


6.Decoder过程
假设Encoder的输出为 m m m,如图,将 m m m输入到Decoder过程中,此时在红框所在的self-attention中,分别是
q = x W Q k = m W K v = m W V \begin{array}{l}{q=x W^{Q}} \\ {k=m W^{K}} \\ {v=m W^{V}}\end{array} q=xWQk=mWKv=mWV

而Decoder最下面的输入为
假设我们现在要翻译一段法语“Je suis etudiant”成英文“I am a student”
而假设目前已经翻译了“I am”,需要对后面进行翻译,那么就将I am转化成词向量输入,在得到I am a之后再次输入,直至完成。
这其中还有一个mask机制,作用是因为我们在训练时需要覆盖还没有输出的单词(通过0,0,0,1,1,1,1,1:1为mask,0为可见)(mask具体是如何表现的,我也有点迷糊,待我研究一下代码再来…)

最后就是Decoder的输出,将蓝色框的向量输入到一个神经网络中去,这个神经网络的输出维度为一个词典的大小,然后经过一个softmax函数,得到概率,取概率最大的作为预测值。

Transformer的损失函数是交叉熵损失。
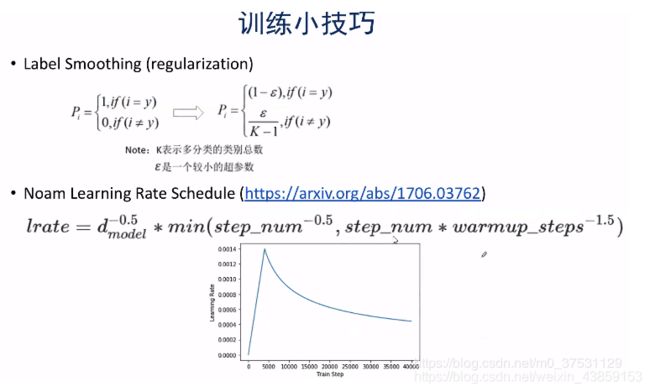
Label smooting: 就是准备标签时不用绝对的0,1序列,可以通过smoothing 也就是正确的值 对应的不是1 而是比如当 ϵ = 0.05 \epsilon=0.05 ϵ=0.05时, 1 − ϵ = 0.95 1-\epsilon=0.95 1−ϵ=0.95 其他的值就是 0.05 K − 1 \displaystyle\frac{0.05}{K-1} K−10.05;
Noam Learing Rate:学习率首先以一个较大的速率增长,达到一定时,以指数的形式进行衰减比较好。
注:上述文章是本人在观看贪心科技视频整理的
链接:https://pan.baidu.com/s/1Ade9NH0D_KiEbKvCTo9UXA 提取码:8J33