机器学习07-支持向量机(SVM)
文章目录
- 优化目标
- 直观上对大间隔的理解
- 大间距分类的数学原理
- 向量内积相关知识
- 数学原理推导
- 核函数1
- 为什么核函数有用
- 核函数2
- SVM参数
优化目标
在逻辑回归中,损失函数定义为:
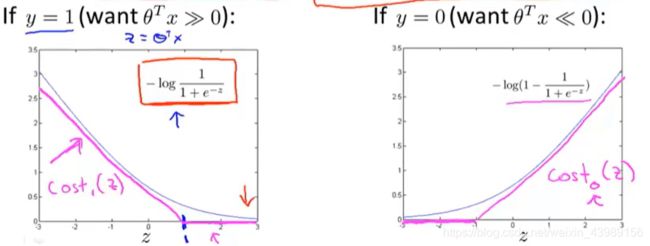
J ( θ ) = − y l o g 1 1 + e − θ T x − ( 1 − y ) l o g ( 1 − 1 1 + e − θ T x ) J(\theta) = -y~log\frac{1}{1+e^{-\theta^Tx}} - (1-y)log(1-\frac{1}{1+e^{-\theta^Tx}}) J(θ)=−y log1+e−θTx1−(1−y)log(1−1+e−θTx1)
此时若将代价函数曲线稍作修改(如上图粉红色曲线)且分别定义为 c o s t 1 ( z ) cost_1(z) cost1(z) 和 c o s t 0 ( z ) cost_0(z) cost0(z),则可构建支持向量机的代价函数:
J ( θ ) = m i n θ C ∑ i = 1 m [ y ( i ) c o s t 1 ( θ T x ( i ) ) + ( 1 − y ( i ) ) c o s t 0 ( θ T x ( i ) ) ] + 1 2 ∑ i = 1 n θ j 2 J(\theta) = min_\theta C\sum_{i=1}^m[y^{(i)}cost_1(\theta^Tx^{(i)})+(1-y^{(i)})cost_0(\theta^Tx^{(i)})]+\frac{1}{2}\sum_{i=1}^n\theta_j^2 J(θ)=minθCi=1∑m[y(i)cost1(θTx(i))+(1−y(i))cost0(θTx(i))]+21i=1∑nθj2
在逻辑回归中,代价函数定义为:
J ( θ ) = m i n θ 1 m [ ∑ i = 1 m y ( i ) ( − l o g h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) ( − l o g ( 1 − h θ ( x ( i ) ) ) ) ] + λ 2 m ∑ j = 1 n θ j 2 J(\theta) = min_\theta\frac{1}{m}[\sum_{i=1}^my^{(i)}(-logh_\theta(x^{(i)}))+(1-y^{(i)})(-log(1-h_\theta(x^{(i)})))] + \frac{\lambda}{2m}\sum_{j=1}^n\theta_j^2 J(θ)=minθm1[i=1∑my(i)(−loghθ(x(i)))+(1−y(i))(−log(1−hθ(x(i))))]+2mλj=1∑nθj2
对比两条式子,可以发现:
-
J S V M ( θ ) J_{SVM}(\theta) JSVM(θ) 少了 1 m \frac{1}{m} m1,我们可以看做是 J S V M ( θ ) J_{SVM}(\theta) JSVM(θ) 是 J l o g i s t i c s ( θ ) J_{logistics}(\theta) Jlogistics(θ) 的 m 倍。而一个式子乘以 m ,其最小值并不会改变,例如:
- m i n u ( ( u − 5 ) 2 + 1 ) → u = 5 min_u((u-5)^2 + 1) \rightarrow u=5 minu((u−5)2+1)→u=5
- m i n u ( 10 ( u − 5 ) 2 + 10 ) → u = 5 min_u(10(u-5)^2 + 10) \rightarrow u=5 minu(10(u−5)2+10)→u=5
-
少了正则化参数 λ \lambda λ ,式子前面多了常数 C。事实上,参数 λ \lambda λ 只是为了平衡两个项之间的关系,从某种意义上来说 A + λ B A + \lambda B A+λB 与 C A + B CA + B CA+B 是一样的,参数 λ \lambda λ 和 C 都是为了平衡 A 与 B 的关系。
此外,与逻辑回归不同的是,SVM并不会输出预测概率,而是通过优化参数 θ \theta θ,直接预测 y 的值,即:
h θ ( x ) = { 1 i f θ T x ≥ 0 0 o t h e r w i s e h_\theta(x) = \begin{cases} 1~~~~if ~~\theta^Tx\geq 0\\ 0~~~~otherwise\\ \end{cases} hθ(x)={1 if θTx≥00 otherwise
直观上对大间隔的理解
支持向量机的代价函数为:
J ( θ ) = m i n θ C ∑ i = 1 m [ y ( i ) c o s t 1 ( θ T x ( i ) ) + ( 1 − y ( i ) ) c o s t 0 ( θ T x ( i ) ) ] + 1 2 ∑ i = 1 n θ j 2 J(\theta) = min_\theta C\sum_{i=1}^m[y^{(i)}cost_1(\theta^Tx^{(i)})+(1-y^{(i)})cost_0(\theta^Tx^{(i)})]+\frac{1}{2}\sum_{i=1}^n\theta_j^2 J(θ)=minθCi=1∑m[y(i)cost1(θTx(i))+(1−y(i))cost0(θTx(i))]+21i=1∑nθj2
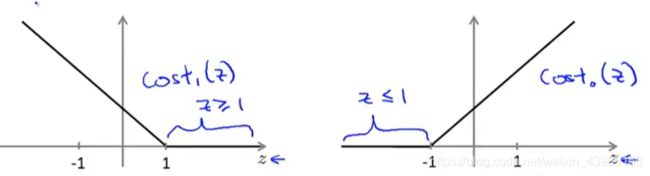
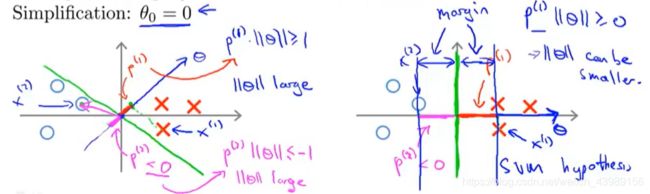
从下图可以看到,当标签 y = 1 时,我们想要 θ T x ( i ) ≥ 1 \theta^Tx^{(i)}\geq 1 θTx(i)≥1 。
当标签 y = 0 时,我们想要 θ T x ( i ) ≤ − 1 \theta^Tx^{(i)}\leq -1 θTx(i)≤−1 。
而事实上,当 θ T x ( i ) ≥ 0 ( y = 1 ) \theta^Tx^{(i)} \geq 0(y=1) θTx(i)≥0(y=1) 或 θ T x ( i ) ≤ 0 ( y = 0 ) \theta^Tx^{(i)} \leq 0(y=0) θTx(i)≤0(y=0) 时就能确保正确分类。但是SVM对此有更高的要求,不是刚好能正确分类就行。令 θ T x ( i ) ≥ 1 ( y = 1 ) \theta^Tx^{(i)} \geq 1(y=1) θTx(i)≥1(y=1)和 θ T x ( i ) ≤ − 1 ( y = 1 ) \theta^Tx^{(i)}\leq -1(y=1) θTx(i)≤−1(y=1) 就相当于给SVM构建了一个安全间距。
现在,假设 C 是一个非常大的值,我们要在SVM上优化代价函数,此时可以把问题看做是通过优化参数 θ \theta θ ,使得代价函数第一项为0,此时 J ( θ ) = m i n θ 1 2 ∑ i = 1 n θ j 2 J(\theta) = min_\theta \frac{1}{2}\sum_{i=1}^n \theta_j^2 J(θ)=minθ21∑i=1nθj2,受以下条件限制:
{ θ T x ( i ) ≥ 1 i f y ( i ) = 1 θ T x ( i ) ≤ − 1 i f y ( i ) = 0 \begin{cases} \theta^Tx^{(i)} \geq 1~~~~~~~if~~y^{(i)} = 1\\ \theta^Tx^{(i)} \leq -1~~~~if~~y^{(i)} = 0 \end{cases} {θTx(i)≥1 if y(i)=1θTx(i)≤−1 if y(i)=0
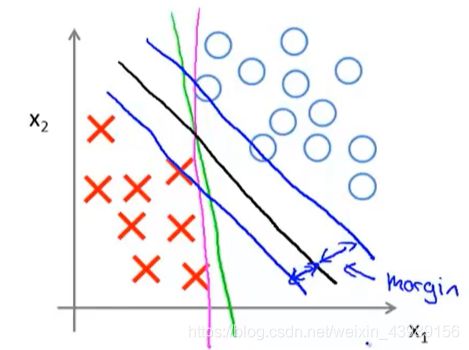
具体的,对于以下数据集,逻辑回归的决策边界可能会是紫色和绿色线,但是SVM会选择黑色线,因为黑色线离正负样本的最小矩离更大,相比之下,紫色和绿色线离样本的最小距离很小,在分离样本时,他们的表现会比黑色线差。黑色线到两条蓝色线的距离称作支持向量机的间距。这使得SVM具有鲁棒性,因为它在分离数据时,会尽量用大的间距去分离。因此SVM也称作大间距分类器。
大间距分类的数学原理
向量内积相关知识
假设有两个向量 u = [ u 1 u 2 ] , v = [ v 1 v 2 ] u = \begin{bmatrix} u_1\\ u_2\\ \end{bmatrix},v = \begin{bmatrix} v_1\\ v_2\\ \end{bmatrix} u=[u1u2],v=[v1v2],则 u 与 v 的内积 u T v u^Tv uTv 如何计算?
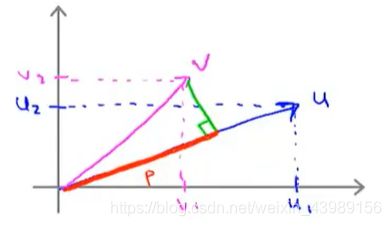
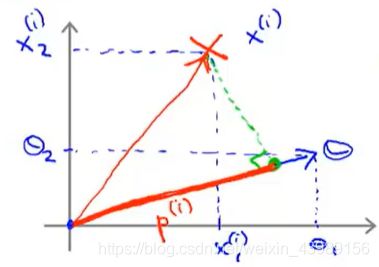
将向量 u 和 v 在图上画出:
u 的范数 ∣ ∣ u ∣ ∣ = u 1 2 + u 2 2 ||u|| = \sqrt {u_1^2+u_2^2} ∣∣u∣∣=u12+u22
将 v 投影到 u 上,计算其长度为 p。注意:p 是有方向的,当 u 与 v 的夹角小于 9 0 ∘ 90^\circ 90∘ 时, p > 0 p > 0 p>0,当 u 与 v 的夹角大于 9 0 ∘ 90^\circ 90∘ 时, p < 0 p < 0 p<0。
则 u T v = p ⋅ ∣ ∣ u ∣ ∣ = u 1 v 1 + u 2 v 2 u^Tv = p \cdot ||u|| = u_1v_1 + u_2v_2 uTv=p⋅∣∣u∣∣=u1v1+u2v2
u T v = v T u u^Tv = v^Tu uTv=vTu,所以也可以把 u 投影到 v 上
数学原理推导
J ( θ ) = m i n θ 1 2 ∑ j = 1 n θ j 2 J(\theta) = min_\theta \frac{1}{2}\sum_{j=1}^n\theta_j^2 J(θ)=minθ21j=1∑nθj2
为了方便,我们令 θ 0 = 0 \theta_0 = 0 θ0=0(即决策边界过原点),n = 2,则:
J ( θ ) = m i n θ 1 2 ( θ 1 2 + θ 2 2 ) = m i n θ 1 2 ( θ 1 2 + θ 2 2 ) 2 = m i n θ 1 2 ∣ ∣ θ ∣ ∣ 2 J(\theta) = min_\theta \frac{1}{2}(\theta_1^2 + \theta_2^2) = min_\theta\frac{1}{2}(\sqrt{\theta_1^2+\theta_2^2})^2 = min_\theta\frac{1}{2}||\theta||^2 J(θ)=minθ21(θ12+θ22)=minθ21(θ12+θ22)2=minθ21∣∣θ∣∣2
类似于 u T v u^Tv uTv, θ T x ( i ) \theta^Tx^{(i)} θTx(i)可看做 x ( i ) x^{(i)} x(i) 到 θ \theta θ 的投影, θ T x ( i ) = p ( i ) ⋅ ∣ ∣ θ ∣ ∣ = θ 1 x 1 ( i ) + θ 2 x 2 ( i ) \theta^Tx^{(i)} = p^{(i)}\cdot ||\theta|| = \theta_1x_1^{(i)} + \theta_2x_2^{(i)} θTx(i)=p(i)⋅∣∣θ∣∣=θ1x1(i)+θ2x2(i)
所以:
J ( θ ) = m i n θ 1 2 ∑ i = 1 n θ j 2 = m i n θ 1 2 ∣ ∣ θ ∣ ∣ 2 J(\theta) = min_\theta \frac{1}{2}\sum_{i=1}^n \theta_j^2 = min_\theta\frac{1}{2}||\theta||^2 J(θ)=minθ21i=1∑nθj2=minθ21∣∣θ∣∣2受以下条件限制:
{ p ( i ) ⋅ ∣ ∣ θ ∣ ∣ ≥ 1 i f y ( i ) = 1 p ( i ) ⋅ ∣ ∣ θ ∣ ∣ ≤ − 1 i f y ( i ) = 0 \begin{cases} p^{(i)}\cdot ||\theta|| \geq 1~~~~~~~if~~y^{(i)} = 1\\ p^{(i)}\cdot ||\theta|| \leq -1~~~~if~~y^{(i)} = 0 \end{cases} {p(i)⋅∣∣θ∣∣≥1 if y(i)=1p(i)⋅∣∣θ∣∣≤−1 if y(i)=0
下图数据集,假设SVM选择左边的决策边界,此时距离决策边界较近的点投影到 θ \theta θ 的距离 p ( i ) p^{(i)} p(i)很短,根据 p ( i ) ⋅ ∣ ∣ θ ∣ ∣ ≥ 1 p^{(i)}\cdot ||\theta|| \geq 1 p(i)⋅∣∣θ∣∣≥1 可得需要较大的 ∣ ∣ θ ∣ ∣ ||\theta|| ∣∣θ∣∣ ,这与 J ( θ ) = m i n θ 1 2 ∣ ∣ θ ∣ ∣ 2 J(\theta) = min_\theta\frac{1}{2}||\theta||^2 J(θ)=minθ21∣∣θ∣∣2 矛盾,所以SVM不会选择左边的决策边界。
事实上,上图中, θ \theta θ 与决策边界是垂直的,因为决策边界为 θ 0 + θ 1 x 1 + θ 2 x 2 = 0 \theta_0 + \theta_1x_1 + \theta_2x_2 = 0 θ0+θ1x1+θ2x2=0(为了简便,这里取 θ 0 = 0 \theta_0 = 0 θ0=0),斜率为 x 2 x 1 = − θ 1 θ 2 \frac{x_2}{x_1} = -\frac{\theta_1}{\theta_2} x1x2=−θ2θ1,而 θ \theta θ 的斜率为 θ 2 θ 1 \frac{\theta_2}{\theta_1} θ1θ2,故两者垂直。
核函数1
对于一个数据集,如果假设函数:
θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 1 x 2 + θ 4 x 1 2 + θ 5 x 2 2 ≥ 0 \theta_0 + \theta_1x_1 + \theta_2x_2 + \theta_3 x_1x_2 + \theta_4x_1^2 + \theta_5x_2^2 \geq 0 θ0+θ1x1+θ2x2+θ3x1x2+θ4x12+θ5x22≥0
成立,则预测 y = 1 y = 1 y=1
我们知道,这些高阶项是获得更多特征的方式,但是我们可以有很多不同的特征选择,或者可能存在比这些高阶多项式更好的特征,因为我们并不知道这些高阶项是不是我们真正需要的。因此我们是否有不同或更好的特征的选择来嵌入到假设函数中?
我们引入一些新的符号:
θ 0 + θ 1 f 1 + θ 2 f 2 + θ 3 f 3 + . . . \theta_0 + \theta_1f_1 + \theta_2f_2 + \theta_3 f_3 + ... θ0+θ1f1+θ2f2+θ3f3+...
这里 f 1 = x 1 , f 2 = x 2 , f 3 = x 1 x 2 , f 4 = x 1 2 , . . . f_1 = x_1,f_2 = x_2, f_3 = x_1 x_2,f_4 = x_1^2,... f1=x1,f2=x2,f3=x1x2,f4=x12,...
有一个可以定义新特征的方法,在这里只使用 f 1 , f 2 . f 3 f_1,f_2.f_3 f1,f2.f3 三个特征,但在实际中可以选择的特征是非常多的。
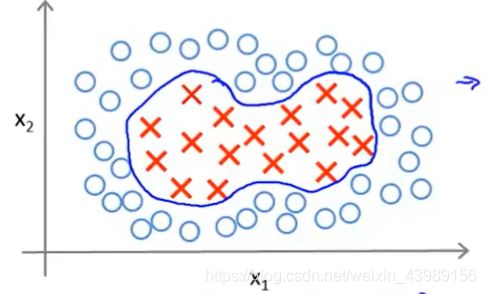
对于 x 1 , x 2 x_1,x_2 x1,x2 (忽略 x 0 x_0 x0),标记三个点 l ( 1 ) , l ( 2 ) , l ( 3 ) l^{(1)},l^{(2)},l^{(3)} l(1),l(2),l(3)
给定一个实例 x,特征 f 1 , f 2 , f 3 f_1,f_2,f_3 f1,f2,f3 定义为:
f 1 = s i m i l a r i t y ( x , l ( 1 ) ) = k ( x , l ( 1 ) ) = e x p ( − ∣ ∣ x − l ( 1 ) ∣ ∣ 2 2 σ 2 ) f_1 = similarity(x,l^{(1)}) = k(x,l^{(1)})= exp(-\frac{||x-l^{(1)}||^2}{2\sigma^2}) f1=similarity(x,l(1))=k(x,l(1))=exp(−2σ2∣∣x−l(1)∣∣2)
f 2 = s i m i l a r i t y ( x , l ( 2 ) ) = k ( x , l ( 2 ) ) = e x p ( − ∣ ∣ x − l ( 2 ) ∣ ∣ 2 2 σ 2 ) f_2 = similarity(x,l^{(2)}) = k(x,l^{(2)})= exp(-\frac{||x-l^{(2)}||^2}{2\sigma^2}) f2=similarity(x,l(2))=k(x,l(2))=exp(−2σ2∣∣x−l(2)∣∣2)
f 3 = s i m i l a r i t y ( x , l ( 3 ) ) = k ( x , l ( 3 ) ) = e x p ( − ∣ ∣ x − l ( 3 ) ∣ ∣ 2 2 σ 2 ) f_3 = similarity(x,l^{(3)}) = k(x,l^{(3)})= exp(-\frac{||x-l^{(3)}||^2}{2\sigma^2}) f3=similarity(x,l(3))=k(x,l(3))=exp(−2σ2∣∣x−l(3)∣∣2)
我们把 k ( x , l ( i ) ) k(x,l^{(i)}) k(x,l(i)) 叫做核函数,这里使用的核函数是高斯函数。
为什么核函数有用
f 1 = s i m i l a r i t y ( x , l ( 1 ) ) = k ( x , l ( 1 ) ) = e x p ( − ∣ ∣ x − l ( 1 ) ∣ ∣ 2 2 σ 2 ) = e x p ( − ∑ j = 1 n ( x j − l j ( 1 ) ) 2 2 σ 2 ) f_1 = similarity(x,l^{(1)}) = k(x,l^{(1)})= exp(-\frac{||x-l^{(1)}||^2}{2\sigma^2}) = exp(-\frac{\sum_{j=1}^n(x_j-l_j^{(1)})^2}{2\sigma^2}) f1=similarity(x,l(1))=k(x,l(1))=exp(−2σ2∣∣x−l(1)∣∣2)=exp(−2σ2∑j=1n(xj−lj(1))2)
当 x ≈ l ( 1 ) x \approx l^{(1)} x≈l(1) :
f 1 ≈ e x p ( − 0 2 σ 2 ) ≈ 1 f_1 \approx exp(-\frac{0}{2\sigma^2}) \approx 1 f1≈exp(−2σ20)≈1
如果 x 远离 l ( 1 ) l^{(1)} l(1):
f 1 = e x p ( − ( l a r g e n u m b e r ) 2 2 σ 2 ) ≈ 0 f_1 = exp(-\frac{(large~~ number)^2}{2\sigma^2}) \approx 0 f1=exp(−2σ2(large number)2)≈0
举个例子:
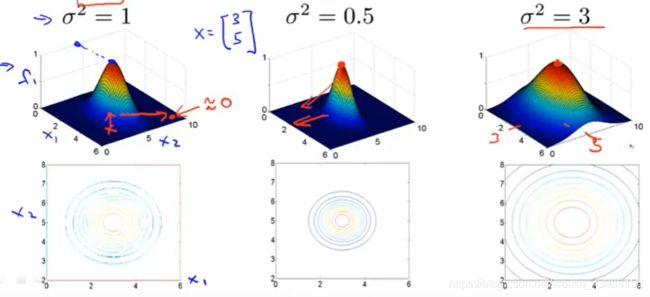
l ( 1 ) = [ 3 5 ] ( 忽 略 x 0 ) , f 1 = e x p ( − ∣ ∣ x − l ( 1 ) ∣ ∣ 2 2 σ 2 ) l^{(1)} = \begin{bmatrix} 3\\ 5\\ \end{bmatrix}(忽略x_0),f_1 = exp(-\frac{||x-l^{(1)}||^2}{2\sigma^2}) l(1)=[35](忽略x0),f1=exp(−2σ2∣∣x−l(1)∣∣2)
对于不同的 σ \sigma σ( σ \sigma σ 为高斯核函数的参数),当 σ \sigma σ 越大, f 1 f_1 f1 下降到 0 的速度越慢。
实例:
当 x(图中玫红色的点)靠近 l ( 1 ) l^{(1)} l(1), f 1 ≈ 1 , f 2 = 0 , f 3 = 0 , θ 0 + θ 1 f 1 + θ 2 f 2 + θ 3 f 3 = − 0.5 + 1 = 0.5 ≥ 0 f_1 \approx 1,f_2 = 0,f_3 = 0,\theta_0 + \theta_1f_1 + \theta_2f_2 + \theta_3 f_3 = -0.5+1 = 0.5 \geq 0 f1≈1,f2=0,f3=0,θ0+θ1f1+θ2f2+θ3f3=−0.5+1=0.5≥0,预测为 1。
当 x(图中蓝色点)远离 l ( 1 ) , l ( 2 ) , l ( 3 ) , l ( 1 ) , f 1 ≈ 0 , f 2 = 0 , f 3 = 0 , θ 0 + θ 1 f 1 + θ 2 f 2 + θ 3 f 3 = − 0.5 < 0 l^{(1)},l^{(2)},l^{(3)},l^{(1)},f_1 \approx 0,f_2 = 0,f_3 = 0,\theta_0 + \theta_1f_1 + \theta_2f_2 + \theta_3 f_3 =-0.5 < 0 l(1),l(2),l(3),l(1),f1≈0,f2=0,f3=0,θ0+θ1f1+θ2f2+θ3f3=−0.5<0,预测为0.
核函数2
给定一个数据集,我们应该如何确定标记点 l ( i ) l^{(i)} l(i)?
我们可以选择数据集中的每一个点(可以来自训练集、验证集或测试集)作为标记点,即令:
l ( 1 ) = x ( 1 ) , l ( 2 ) = x ( 2 ) , . . . , l ( m ) = x ( m ) l^{(1)} = x^{(1)},l^{(2)} = x^{(2)},...,l^{(m)} = x^{(m)} l(1)=x(1),l(2)=x(2),...,l(m)=x(m)
对于训练样本 ( x ( i ) , y ( i ) ) (x^{(i)},y^{(i)}) (x(i),y(i)),有:
f 1 ( i ) = s i m ( x ( i ) , l ( 1 ) ) f_1^{(i)} = sim(x^{(i)},l^{(1)}) f1(i)=sim(x(i),l(1))
f 2 ( i ) = s i m ( x ( i ) , l ( 2 ) ) f_2^{(i)} = sim(x^{(i)},l^{(2)}) f2(i)=sim(x(i),l(2))
⋮ \vdots ⋮
f i ( i ) = s i m ( x ( i ) , l ( i ) ) = e x p ( − 0 2 σ 2 ) = 1 f_i^{(i)} = sim(x^{(i)},l^{(i)}) = exp(-\frac{0}{2\sigma^2}) = 1 fi(i)=sim(x(i),l(i))=exp(−2σ20)=1
⋮ \vdots ⋮
f m ( i ) = s i m ( x ( i ) , l ( m ) ) f_m^{(i)} = sim(x^{(i)},l^{(m)}) fm(i)=sim(x(i),l(m))
f ( i ) = [ f 0 ( i ) f 1 ( i ) ⋮ f m ( i ) ] f^{(i)} = \begin{bmatrix} f_0^{(i)}\\ f_1^{(i)}\\ \vdots\\ f_m^{(i)}\\ \end{bmatrix} f(i)=⎣⎢⎢⎢⎢⎡f0(i)f1(i)⋮fm(i)⎦⎥⎥⎥⎥⎤
训练:
J ( θ ) = m i n θ C ∑ i = 1 m [ y ( i ) c o s t 1 ( θ T f ( i ) ) + ( 1 − y ( i ) ) c o s t 0 ( θ T f ( i ) ) ] + 1 2 ∑ i = 1 n θ j 2 J(\theta) = min_\theta C\sum_{i=1}^m[y^{(i)}cost_1(\theta^Tf^{(i)})+(1-y^{(i)})cost_0(\theta^Tf^{(i)})]+\frac{1}{2}\sum_{i=1}^n\theta_j^2 J(θ)=minθCi=1∑m[y(i)cost1(θTf(i))+(1−y(i))cost0(θTf(i))]+21i=1∑nθj2
SVM参数
- C ( = 1 λ ) C(=\frac{1}{\lambda}) C(=λ1):很大:低偏差,高方差(过拟合)
- 很小:高偏差,低方差(欠拟合)
- σ 2 \sigma^2 σ2:很大:变化平缓,高偏差,低方差
- 很小:变化迅速,低偏差,高方差