自然语言处理之维特比算法实现中文分词

维特比(viterbi)算法介绍

        维特比算法是一种动态规划算法用于寻找最有可能产生观测事件序列的-维特比路径-隐含状态序列，可以解决任何一个图中的最短路径问题，特别是在马尔可夫信息源上下文和隐马尔可夫模型中。 术语“维特比路径”和“维特比算法”也被用于寻找观察结果最有可能解释相关的动态规划算法。例如在统计句法分析中动态规划算法可以被用于发现最可能的上下文无关的派生(解析)的字符串，有时被称为“维特比分析”
        在隐马尔科夫链中，任意时刻t下状态的值有多个，以拼音转汉字为例，输入拼音为“yike”可能有的值为一棵，一刻或者是一颗等待，用符号xij表示状态xi的第j个可能值，将状态序列按值展开，就得到了一个篱笆网（特殊的图——篱笆网络的有向图（Lattice )）了，这也就是维特比算法求解最优路径的图结构。

       隐马尔科夫的预测问题就是要求图中的一条路径，使得该路径对应的概率值最大。 对应上图来讲，假设每个时刻x可能取的值为3，如果直接求的话，有3^N的组合数，底数3为篱笆网络宽度，指数N为篱笆网络的长度，计算量非常大。维特比利用动态规划的思想来求解概率最大路径（可理解为求图最短路径），使得复杂度正比于序列长度，复杂度为O(N⋅D⋅D), N为长度，D为宽度，从而很好地解决了问题的求解。

算法思路

输入：模型$$P(A\mid B)=\frac{P(B\mid A)P(A)}{P(B)}$$和观测$$O=\left(o_1,o_2,\cdots ,o_T\right)$$

输出：最优路径$$I^{\ast }=\left(i_1^{\ast },i_2^{\ast },\cdots ,i_T^{\ast }\right)$$
（1）初始化$${\delta }_1(i)={\pi }_i{b}_i\left(o_1\right),i=1,2,\cdots ,N$$
$${\psi }_1(i)=0,i=1,2,\cdots ,N$$

（2）递推。对t=2,3，…，T
$${\delta }_t(i)=\underset{1⩽j<N}{\max }\left[{\delta }_{t-1}(j)a_{ji}\right]b_i\left(o_t\right),i=1,2,\cdots ,N$$
$${\psi }_t(i)=\arg \underset{1\le j\le N}{\max }\left[{\delta }_{t-1}(j)a_{jt}\right],i=1,2,\cdots ,N$$

（3）终止$$P^{\ast }=\underset{1\le i⩽N}{\max }{\delta }_T(i)$$
$$i_T^{\ast }=\arg \underset{1⩽i⩽N}{\max }\left[{\delta }_T(i)\right]$$

分词实例

class HMM(object):

    # 初始化一些全局信息
    def __init__(self):

        import os
        # 主要是用于存取算法中间结果，不用每次都训练模型
        self.model_file = './hmm_model.pkl'
        # 状态值集合
        self.state_list = ['B', 'M', 'E', 'S']
        # 参数加载,用于判断是否需要重新加载model_file
        self.load_para = False


    # 用于加载已计算的中间结果，当需要重新训练时，需初始化清空结果
    def try_load_model(self, trained):
        if trained:
            import pickle
            with open(self.model_file, 'rb') as f:
                self.A_dic = pickle.load(f)
                self.B_dic = pickle.load(f)
                self.Pi_dic = pickle.load(f)
                self.load_para = True

        else:
            # 状态转移概率（状态->状态的条件概率）
            self.A_dic = {}
            # 发射概率（状态->词语的条件概率）
            self.B_dic = {}
            # 状态的初始概率
            self.Pi_dic = {}
            self.load_para = False

    # 计算得到HMM所需要的转移概率、发射概率以及初始概率
    def train(self, path):

        # 重置几个概率矩阵
        self.try_load_model(False)
        # 统计状态出现次数，求p(o)
        Count_dic = {}

        # 初始化参数函数
        def init_parameters():
            for state in self.state_list:        
                self.A_dic[state] = {s: 0.0 for s in self.state_list}
                self.Pi_dic[state] = 0.0
                self.B_dic[state] = {}
                Count_dic[state] = 0

        # 为每个读进来的字打标签，也即是状态值
        def makeLabel(text):
            out_text = []
            if len(text) == 1:
                out_text.append('S')
            else:
                # 列表的加操作，也即是列表的元素扩展
                out_text += ['B'] + ['M'] * (len(text) - 2) + ['E'] 
            return out_text

        init_parameters()
        #print('init_parameters:',self.A_dic)
        line_num = -1
        # 观察者集合，主要是字以及标点等
        words = set()
        with open(path, encoding='utf8') as f:
            for line in f:
                line_num += 1
                #if line_num==2:  # 测试用
                    #break
                line = line.strip() # 用于移除字符串头尾指定的字符（默认为空格或换行符）或字符序列
                #print('here:',line)
                if not line:
                    continue
                word_list = [i for i in line if i != ' ']
                #print('word_list:',word_list)
                words |= set(word_list)  # 更新字的集合,这里用的是集合的并操作
                linelist = line.split()  # 按空格分割字串
                #print('there:',linelist)
                line_state = []
                for w in linelist:
                    line_state.extend(makeLabel(w))
                #print('line_state:',line_state)
                assert len(word_list) == len(line_state)

                for k, v in enumerate(line_state): # 这里的k：元素下标  v：元素值
                    #print('k,v:',k,v)
                    Count_dic[v] += 1
                    if k == 0:
                        self.Pi_dic[v] += 1  # 每个句子的第一个字的状态，用于计算初始状态概率
                    else:
                        # 计算转移pinlv：[line_state[k - 1]][v]用的非常好
                        self.A_dic[line_state[k - 1]][v] += 1                       
                        #print('B_dic[line_state[k]]:',self.B_dic[line_state[k]].get(word_list[k], 0))
                        # 计算发射频率,dict.get(key, default=None)
                        self.B_dic[line_state[k]][word_list[k]] = \
                            self.B_dic[line_state[k]].get(word_list[k], 0) + 1.0  
                        #print('self.B_dic:',self.B_dic)                
                #print('A_dic:\n',self.A_dic)

        #print('self.Pi_dic:',self.Pi_dic)
        # 计算初始概率：用每行开头字的状态值除以所有行
        self.Pi_dic = {k: v * 1.0 / line_num for k, v in self.Pi_dic.items()}
        #print('self.Pi_dic:',self.Pi_dic)
        #print('Count_dic:',Count_dic)
        # 状态转移概率:4x4的矩阵的每一个转移状态值除以该状态出现的总数(count(M/B)/count(B))
        self.A_dic = {k: {k1: v1 / Count_dic[k] for k1, v1 in v.items()}
                      for k, v in self.A_dic.items()}
        #print('self.A_dic~:',self.A_dic)
        #加1平滑(发射概率计算同状态转移计算方式大致一样)
        self.B_dic = {k: {k1: (v1 + 1) / Count_dic[k] for k1, v1 in v.items()}
                      for k, v in self.B_dic.items()}
        #序列化
        import pickle
        with open(self.model_file, 'wb') as f:
            pickle.dump(self.A_dic, f)
            pickle.dump(self.B_dic, f)
            pickle.dump(self.Pi_dic, f)

        # 返回对象本身
        return self
    #代码实现维特比算法
    def viterbi(self, text, states, start_p, trans_p, emit_p):      
        #print('start_p:',start_p,'\n','trans_p:', trans_p,'\n','emit_p:',emit_p)
        V = [{}]
        path = {}
        for y in states: 
            #print('TT:',emit_p[y].get(text[0], 0))
            V[0][y] = start_p[y] * emit_p[y].get(text[0], 0)
            path[y] = [y]

        for t in range(1, len(text)):
            V.append({})
            newpath = {}

            # 检验训练的发射概率矩阵中是否有该字
            neverSeen = text[t] not in emit_p['S'].keys() and \
                text[t] not in emit_p['M'].keys() and \
                text[t] not in emit_p['E'].keys() and \
                text[t] not in emit_p['B'].keys()
            #print(text[t],neverSeen)
            for y in states:
                #设置未知字单独成词
                emitP = emit_p[y].get(text[t], 0) if not neverSeen else 1.0 
                (prob, state) = max([(V[t - 1][y0] * trans_p[y0].get(y, 0) *emitP, y0)
                     for y0 in states if V[t - 1][y0] > 0])
                #print('prob:',prob,'state:',state,'——>',y)              
                V[t][y] = prob
                #print('V[t]:~',V[t])
                newpath[y] = path[state] + [y]        
                #print('newpath:',newpath)
            path = newpath

        if emit_p['M'].get(text[-1], 0)> emit_p['S'].get(text[-1], 0):
            (prob, state) = max([(V[len(text) - 1][y], y) for y in ('E','M')])
        else:
            (prob, state) = max([(V[len(text) - 1][y], y) for y in states])

        return (prob, path[state])

    def cut(self, text):
        import os
        if not self.load_para:
            self.try_load_model(os.path.exists(self.model_file))
        prob, pos_list = self.viterbi(text, self.state_list, self.Pi_dic, self.A_dic, self.B_dic) 
        begin, next = 0, 0    
        for i, char in enumerate(text):
            pos = pos_list[i]                                                 
            if pos == 'B':
                begin = i
            elif pos == 'E':
                yield text[begin: i+1]
                next = i+1
            elif pos == 'S':
                yield char
                next = i+1
        if next < len(text):
            yield text[next:]

通过调用上述方法对人民日报的分词语料进行训练，最终打印了一下原文以及分词后的结果

hmm = HMM()
#模型训练，数据使用的是人民日报的分词预料
hmm.train('./trainCorpus.txt_utf8')
#hmm.train('./test.txt_utf8')

text = '这是一个非常棒的方案！'
res = hmm.cut(text)
print(text)
print(str(list(res)))

最终结果如下，这里使用的的是对人民日报的分词进行训练的。

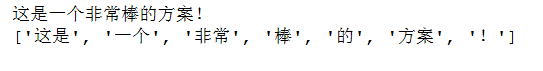
最后说明一点本章节代码来自涂铭老师的《Python自然语言处理实战核心技术与算法》一书。