「周练」Codeforces Round #530 (Div. 2)
目录
- 一. Codeforces Round #530 (Div. 2)
- A. Snowball (模拟)
- B. Squares and Segments (数学)
- C. Postcard (贪心)
- D. Sum in the tree (dfs+贪心)
- E. Nice table (找规律+模拟)
- F. Cookies (树形dp+线段树)
- 二. 二分练习
- A. Aggressive cows (最大化最小值)
- B. String Game (二分下标)
- C. Delivering Carcinogen (二分+计算几何)
一. Codeforces Round #530 (Div. 2)
比赛网址链接:Codeforces Round #530 (Div. 2)
A. Snowball (模拟)
题意
一个重量为 w w w 的雪球从高度 h h h 滚下,每下降一单位,重量的增加量为当前高度,过程有两个石头,雪球经过石头重量的减少量为石头的重量,问雪球到达地面时的重量
思路
按照题意模拟即可,注意过程重量不会减成负值
代码
#include B. Squares and Segments (数学)
题意
给一个数 n n n,找出两个数,使得它们的乘积不小于 n n n,要求最小化这两个数的和
思路
开始读错题了,以为要用这 n n n 个小正方形组成一个矩形,后来发现不是,那就好办了,最小化两个数的和,肯定这两个数要比较接近,那就不断增大两个数,知道它们的乘积不小于 n n n 即可
代码
#include C. Postcard (贪心)
题意
一个字符串里有小写字母、 ∗ * ∗ 符号、 ? ? ? 符号,这两种符号都可以将它们前方的字母删除、保留,不同的是 ∗ * ∗ 符号还可以无穷多次复制其前面的字母,问这个串能否构造出一个长度为 k k k 的串
思路
首先考虑不存在的情况,那就只有两种情况,一是字符串里没有 ∗ * ∗ 符号,但 k k k 太大,二是 k k k 太小,能删的全删也构造不出长度为 k k k 的。
之后就分类讨论就好,根据原串我们统计的信息,如果 k k k 比较大,那就确定好要复制的字母和个数,剩下的字母都保留即可,如果 k k k 比较小,那就确定要删除的字母个数,先删够,剩下的字母都保留即可
代码
#include D. Sum in the tree (dfs+贪心)
题意
现在有一棵树,根为 1 1 1, i i i 号结点的权值为 a i a_i ai, s i s_i si 为 i i i 号结点到根路径上的总权值,现在只知道深度为奇数的结点的 s i s_i si 值,让你推出 所有结点的 a i a_i ai 值,要求它们的 a i a_i ai 总和最小
思路
我们会发现一个规律就是,给越靠近根的结点赋值越大,它们的子孙赋值就越小,那么 a i a_i ai 总和就会越小,所以我们要想办法把靠近根的结点赋上尽可能大的值,离根越远的赋尽可能小的值
对于 − 1 -1 −1 的情况肯定就是对于某一个结点,存在一个子孙结点的 s i s_i si 值比其本身的要小,因为 a i a_i ai 非负,所以从根到叶子的路径 s i s_i si 值肯定不会递减。然后我们尝试还原深度为偶数的每个点的 s i s_i si 值。
根据前面的分析,很容易得出 s u = m i n ( s v ) ( v 是 u 的 儿 子 ) s_u=min(s_v)(v是u的儿子) su=min(sv)(v是u的儿子),也就是儿子共享的部分,这部分给父亲,让父亲赋更大的值,如果叶子所在层也为偶数层的话其 a i a_i ai 值显然赋 0 最优,所以其 s i s_i si 的值应和父亲的相同,知道了所有结点的 s i s_i si 值, a i a_i ai 就很好求了
代码
#include E. Nice table (找规律+模拟)
题意
一个 n × m n×m n×m 矩阵,要求最小的修改次数使得矩阵的所有 2 × 2 2×2 2×2 的子矩阵都包含 A , T , G , C A,T,G,C A,T,G,C 四个字母
思路
找规律会发现有两种情况:
1.每行都是两个固定字符交替组成,且相邻两行的字符交集为空
例如:

2.每列都由两个固定字符交替组成,且相邻两列的字符交集为空
例如:

那就枚举交替的行或列,找出替换最小的那组
代码
#include F. Cookies (树形dp+线段树)
题意
给你一棵树,树上有 n n n 个节点,每个节点上有 x i x_i xi 块饼干,吃在这个节点上的每块饼干需要花费的时间为 t i t_i ti,有两个玩家,玩家一每次的操作是:移动到当前点的子节点或者申请游戏结束返回根节点并选择性的吃沿途的饼干,玩家二的操作是:在玩家一操作后删除当前点到儿子节点的一条边,走路和吃饼干都消耗时间,会给出一个总时间,在总时间内尽可能的多吃饼干,问最多能吃多少个?
思路
首先我们可以维护出玩家一在每个结点返回所能吃的最大饼干数,设 f u f_u fu 为玩家一在 u u u 号结点结束游戏返回根所能吃到的最多饼干数,为什么可以维护呢?因为固定结点时,其到根的距离所花时间我们可以很容易求出来,然后 总时间减去路径花费时间的两倍(去和返) 剩下的时间即为玩家一可以在返回路径上吃饼干的时间,最优策略肯定是先吃这个路径上单位花时间少的饼干,吃完再吃次小的…依次类推,暴力去路径找的花太费时,所以可以选择合适的数据结构来维护路径上饼干的信息,可以用线段树,开始想用树状数组来着,但是遇到了问题,因为玩家一可能在一个节点只吃部分饼干,用线段树的话就 依照饼干所花时间建立线段树,线段树结点维护两个信息,一个是这个结点所维护的时间段吃掉所有饼干所需花费的总时间,一个是这个时间段的饼干总个数。
下一步,我们不妨定义: d p u dp_u dpu 从结点 u u u 向下走最多可以吃到多少饼干,由于是玩家一先手,那么最开始的最大边则不会被删除,但之后路途的最大边都会被玩家二删除,所以很容易得到递推式:
d p u = m a x ( f u , d p v ) ( u 为 根 , v 为 u 的 儿 子 且 d p v 为 u 儿 子 中 最 大 的 那 个 ) dp_u=max(f_u,dp_v)(u为根,v为u的儿子且dp_v为u儿子中最大的那个) dpu=max(fu,dpv)(u为根,v为u的儿子且dpv为u儿子中最大的那个)
d p u = m a x ( f u , d p v ) ( u 非 根 , v 为 u 的 儿 子 且 d p v 为 u 儿 子 中 次 大 的 那 个 ) dp_u=max(f_u,dp_v)(u非根,v为u的儿子且dp_v为u儿子中次大的那个) dpu=max(fu,dpv)(u非根,v为u的儿子且dpv为u儿子中次大的那个)
值得注意的是: d p u = f u ( u 为 叶 子 ) dp_u=f_u(u为叶子) dpu=fu(u为叶子)
d p 1 即 为 最 终 结 果 dp_1即为最终结果 dp1即为最终结果
代码
#include 二. 二分练习
A. Aggressive cows (最大化最小值)
题目链接
POJ 2456
题意
x x x 坐标轴有 n n n 个牛舍,现在给 m m m 头牛分配牛舍,问怎样分配使得任意两头牛的距离最大化
思路
二分一下任意两头牛的最小距离,从前往后贪心的填即可
代码
#include B. String Game (二分下标)
题目链接
CodeForces - 779D
题意
一个字符串 s s s,现在有一个删除序列,问按照这个删除序列执行,最多执行几次,原序列仍有 t t t 字符串的子序列
思路
二分这个删除序列的下标,看以这个下标为终点对 s s s 串进行删除,剩下的串能否找出一个子序列为 t t t
代码
#include C. Delivering Carcinogen (二分+计算几何)
题目链接
CodeForces - 199E
题意
有一颗行星 P P P 围绕一颗恒星 D D D 以恒定速度 v p v_p vp 逆时针旋转,绕行半径为 R R R,现在有一艘飞船(初始位置给出)要去 行星 P P P 上,且要求任何时刻都不能处在 以恒星 D D D 为中心,半径为 r r r 的范围内,让你求到达行星 P P P 的最短时间
思路
对于一个确定时间 t t t,行星的位置确定,飞船到达行星的时间取决于其运行路线,如果以最短路线前往 P P P,花费时间为 t 1 t_1 t1,只要 t 1 t_1 t1 不大于 t t t,就一定可以到达 P P P,所以可以对时间二分,来寻找最短时间。
对于确定的时间 t t t,现在有几个问题需要解决:
- 给出行星的初始坐标,经过时间 t t t 后的具体坐标
- 确定行星的位置后,飞船的最短距离的确定与计算
(1) 对于前者,确定其逆时针旋转多少度即可
推导过程如下:

设原向量 p 1 p_1 p1 坐标 ( x 1 , y 1 ) (x_1,y_1) (x1,y1),长度为 R R R ,与 x x x 轴夹角为 A A A,逆时针旋转 B B B 角度后的坐标为 ( x 2 , y 2 ) (x_2,y_2) (x2,y2),则有:
x 2 = R c o s ( A + B ) x_2=Rcos(A+B) x2=Rcos(A+B)
= R c o s ( A ) c o s ( B ) − R s i n ( A ) s i n ( B ) =Rcos(A)cos(B)-Rsin(A)sin(B) =Rcos(A)cos(B)−Rsin(A)sin(B)
= x 1 c o s ( B ) − y 1 s i n ( B ) =x_1cos(B)-y_1sin(B) =x1cos(B)−y1sin(B)
y 2 y_2 y2 同理:
y 2 = R s i n ( A + B ) y_2=Rsin(A+B) y2=Rsin(A+B)
= R s i n ( A ) c o s ( B ) + R c o s ( A ) s i n ( B ) =Rsin(A)cos(B)+Rcos(A)sin(B) =Rsin(A)cos(B)+Rcos(A)sin(B)
= y 1 c o s ( B ) + x 1 s i n ( B ) =y_1cos(B)+x_1sin(B) =y1cos(B)+x1sin(B)
(2) 对于后者,比较麻烦。要先确定是否可以直线到达,或者是中间需要绕着走,这取决于 飞船与行星的距离 和 两者关于内圆的切线段长度和 谁大谁小

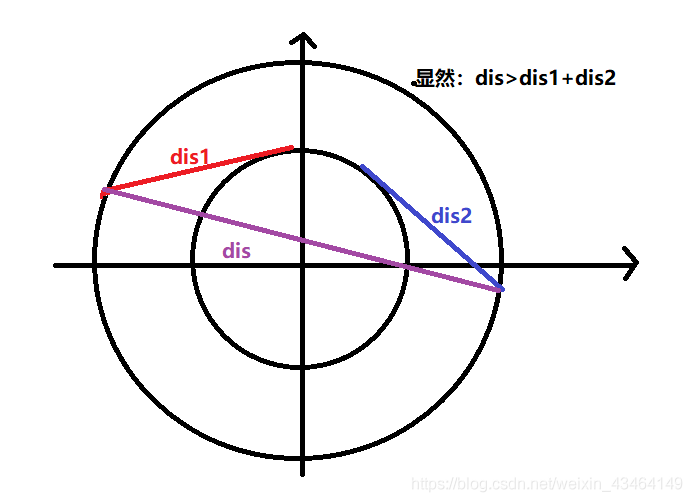
直线走的话就直接拿两点距离除以飞船速度可得最短时间,如果需要绕行的话,需要计算中间那段绕内圆的弧长,弧度的计算是先计算 飞船与行星关于原点的夹角 ,可根据余弦定理来求(飞船 行星和原点组成一个三角形,知道三边可求任意夹角),然后计算 飞船与切点关于圆心的夹角 和 行星与切点关于圆心的夹角,这个很好求。然后求得的大角减去两个小角即为我们要的那段弧的弧度,乘上半径即为距离。

代码
#include