【基础知识】HTML5 Canvas 学习Canvas需要的数学知识:代数方程、三角函数、向量运算等(图文、举例)
我的处女作《Canvas系列教程》在我的Github上正在连载更新,希望能得到您的关注和支持,让我有更多的动力进行创作。
教程介绍、教程目录等能在README里查阅。
传送门:https://github.com/827652549/CanvasStudy
目录
为什么要数学知识
需要有哪些数学基础?
1.求解代数方程
2.三角函数
2.1角的度量:角度和弧度
2.2正弦、余弦和正切函数
3.向量运算
3.1向量的大小
3.2单位向量
3.3向量的加法与减法
3.4两个向量的点积
4.根据计量单位来推导等式
为什么要数学知识
如果想那个用Canvas实现一些有趣的功能,那么必须要很好地了解一些基本的数学知识,尤其是代数方程、三角函数及向量运算。如果要编写类似电子游戏那样更为复杂的应用程序,那么还需要掌握如何根据给定的计量单位来推导等式。
需要有哪些数学基础?
- 求解代数方程
- 三角函数
- 向量运算
- ……
1.求解代数方程
对于任意的代数方程,如(10x+5)*2=110;都可以进行如下操作使等式仍然成立:
- 等式两端同时加上任意一个实数
- 等式两端同时减去任意一个实数
- 等式两端同时乘以任意一个实数
- 等式两端同时除以任意一个实数
- 等式一端或两端同时是乘以或除以1
最后一条看上去很奇怪,为什么要给登时的一段或两端同时乘以或除以1呢?
在后面的学习中,将会用到根据计量单位来推导公式,就会看到如何恰当地用到这条简单的规则。(等我写到那个章节,再把链接贴到此处)
2.三角函数
即使是简单地使用Canvas,也需要对三角函数要有个基本的了解。举例来说,对于绘制多边形,就要多正弦和余弦函数有一定了解。
2.1角的度量:角度和弧度
Canvas中所有与角有关的API,都以弧度(radian)的方式来指定该角的值。JavaScript中的Math.sin();Math.cos();Math.tan();函数也都采用弧度值。
180度=π弧度
例如:π约等于3.14,所以,45度等于(3.14/180)*45度,经过运算可知,等于0.7853弧度
提示:π可以直接使用Math.PI来表示
2.2正弦、余弦和正切函数
这些是基础中的基础,必须要会。
cos(θ)=邻边/斜边
sin(θ)=对边/斜边
tan(θ)=对边/邻边
3.向量运算
向量的存在,能给我们的程序带来物理世界的特性。
二维向量都含有两个值:方向(direction)和大小(magnitude)。这两个值可以表达出各种各样的物理特性来,比如力(force)和运动(motion)。有了力和运动,便可以实现真实碰撞效果等等。
其他较为复杂的使用:SAT(分离轴定理)
后面的专栏博文中我会详细介绍这个定理,并把链接贴到此处,尽请持续关注。
3.1向量的大小
虽说二维向量的大小与方向是这两个数值进行建模的,不过通常情况下,根据给定x与y的值来计算这两个数值的其中一个,也是很有用的。
如勾股定理。
var vevtorMagnitude=Math.sqrt(Math.pow(vector.x,2)+Math.pow(vector.y,2));上述代码片段可以从一个名为vector的向量引用中计算出该向量的大小。
3.2单位向量
向量运算经常会用到一个名为“单位向量”(unit vector)的东西。可以理解为一种只用来只是方向的向量。
之所以叫它单位向量,是因为其长度永远是“单位1”(1 unit)。如果根据给定的向量来计算其单位向量,需要把原来的向量大小去掉,只留下方向即可。在JavaScript代码中,可以这么做。
var vectorMagnitude = Math.sqrt(Math.pow(vector.x, 2) + Math.pow(vector.y, 2)),
//新单位向量
unitVector = new Vector();
//新单位向量上的x值
unitVector.x = vector.x / vectorMagnitude;
//新单位向量上的y值
unitVector.y = vector.y / vectorMagnitude;3.3向量的加法与减法
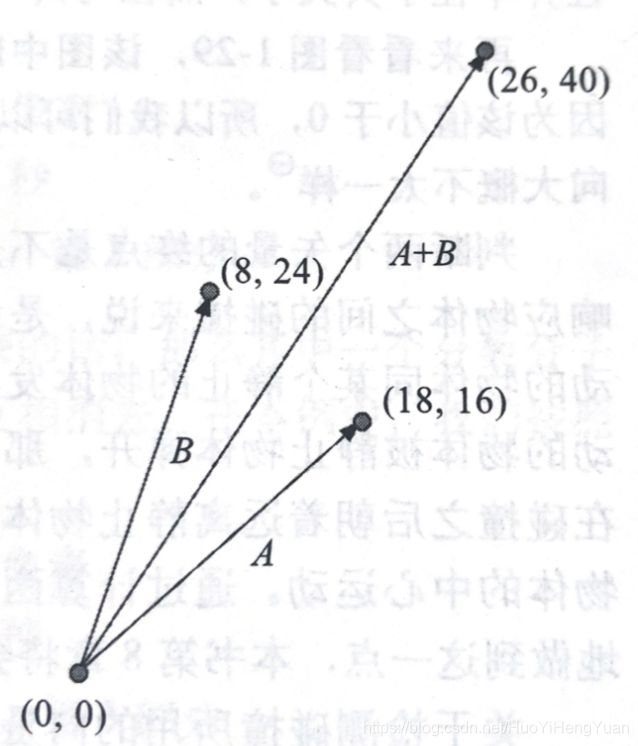
向量的加减法也很有用,举例来说,如果两个力同时作用某个物体,你可以把代表这两个力的向量想家,计算出这两个力的合力。同样,也可以从一个方位向量中减去另一个,以求得两点之间的边界。
图演示了向量的加法运算
向量的加法用代码表示
var vectorSum = new Vector();
vectorSum.x = vectorA.x+vectorB.x;
vectorSum.y = vectorA.y+vectorB.y;向量的减法也很简单
var vectorSubtraction = new Vector();
vectorSubtraction.x = vectorA.x - vectorB.x;
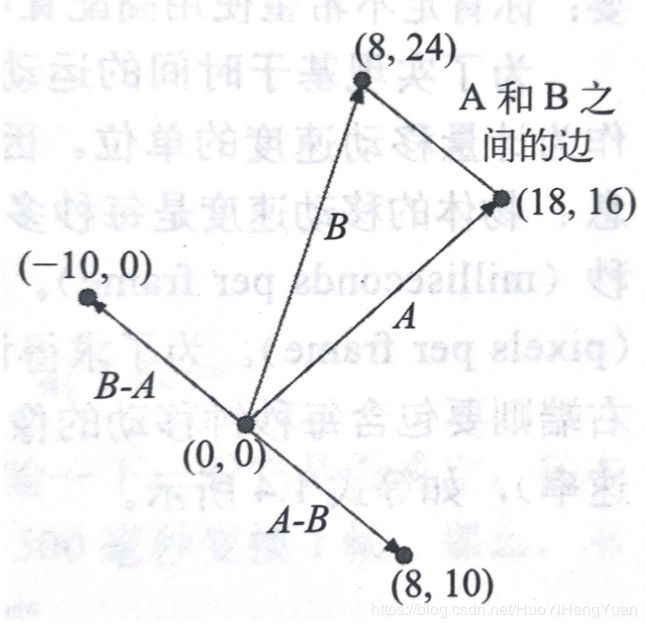
vectorSubtraction.y = vectorA.y - vectorB.y;下图演示了将一个向量从另一个之中减去所得到到第三个向量,其方向恰好与两向量终点之间到边界方向是一致的。在图中,向量A-B与B-A相互平行,且二者都平行于向量A、B所构成都“边向量”。
3.4两个向量的点积
向量的点积可以精确控制,“当运动的物体碰撞静止的物体时,静止的物体朝着远离运动物体方向运动”这种情景。
先看一下点积的求法:
向量的点积等于两个向量对应分量相乘,然后再将乘积相加。
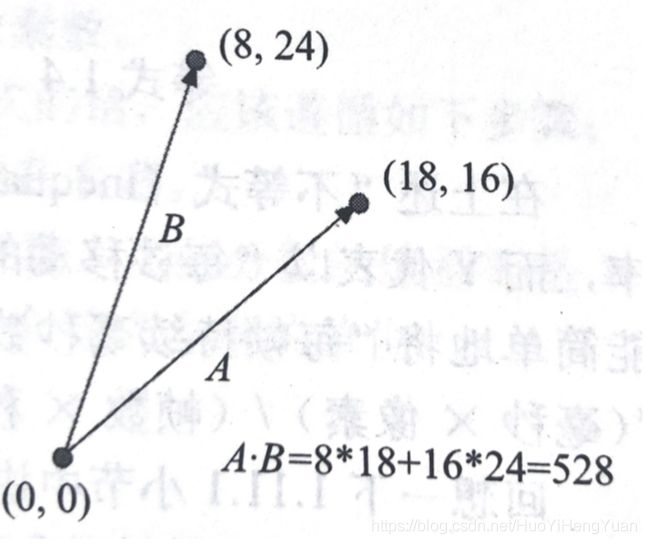
var dotProduct = vectorA.x * vectorB.x + vectorA.y * vectorB.y;更直观的效果如图所示。
注意:于两个向量加减法运算结果不同,点积不是向量。
专业人士把这种值叫做“标量”(scalar,也叫做“纯量”)
就是说,它仅仅一个数字而已, 但是,它的意义不在于528这个点积结果的值的大小,而在于它的“大于0”这个事实,意味着这两个向量大概处于同一方向。
再来看看下图的两个向量,点积为-528,因为该值小于0,所以我们可以推测出,这两个向量所指的方向大概不太一样。
如果两个向量点积为0,则其必定相互垂直。
4.根据计量单位来推导等式
动画的移动应该是以时间为基准的,因为一个物体的移动频率应该随着动画的帧速率而改变,基于时间的运动(time-based motion)对于多人游戏来说尤为重要,你肯定不希望高配置电脑的玩家比别人移动地更快。
现在,我们知道两个信息:
-
每秒钟移动的像素数(pixels per second)
-
当前动画的帧速率(frame rate):每帧持续多少毫秒(milliseconds per frame)
我们要计算:每帧移动的像素数
需要经过1秒=1000毫秒的转化,然后得出以下结论
像素/帧=(用像素/秒表示的速度)*(用毫秒/帧表示的帧速率)/1000
上面就是我们最后得到的推导公式,建议推导完成后代入一些简单数值来检验以下,看它是否成立。
这里插入一句话:学习程序,需要注意下这些专有名词的英文表示,为之前就踩过一个英文单词的坑:
帧(frame):之前有个做过的项目,是关于流媒体的javaCV项目的案例代码,有个导入的JavaCV包里的“Frame”类,误把它当作java.awt.Frame,之前没做过这类项目,所以还是小白一个,后来才知道这个是“帧”的意思,当时还苦恼自己看不到图形界面,以为出了bug。