树状数组1——树状数组入门
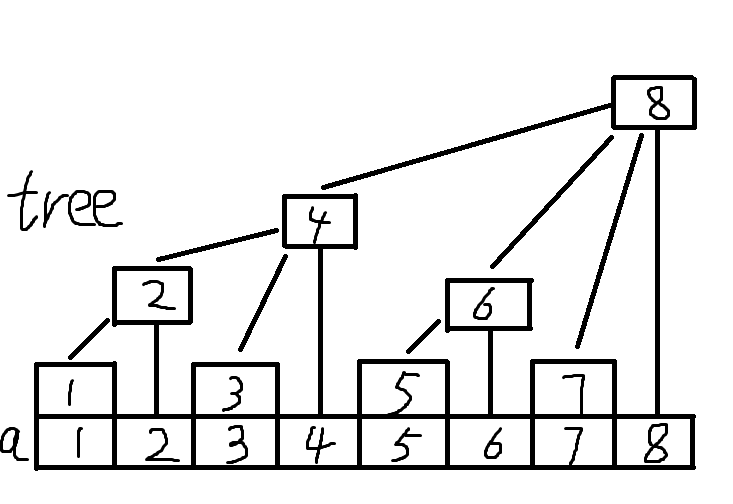
先上一发树状数组的经典图片吧:
仔细看一下,发现tree的每一个节点的高度并不是随意的,而是由它转成二进制之后末尾连续零的数量决定的,连续零的数量加1,就是高度,例如:
3->11 零的数量为0,加1等于1,所以它的高度就是1
6->110 零的数量为1,加1等于2,所以它的高度就是2
8->1000 零的数量为3,加1等于4,所以它的高度就是4
我们看一下tree数组中每一个数记录了a中那些数的和:
tree[1]=a[1]
tree[2]=a[1]+a[2]
tree[3]=a[3]
tree[4]=a[1]+a[2]+a[3]+a[4]
tree[5]=a[5]
tree[6]=a[5]+a[6]
tree[7]=a[7]
tree[8]=a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]+a[8]
可以发现,tree中的每一个节点管理的a都是连续的,具体一点,它管理的数就是在它前面的高度比它大的第一个tree节点的后一个到它自己,比如6,前面的比它高的第一个就是4,4的后一个是5,它自己是6,所以它管理5~6
那这个“在它前面的高度比它大的第一个tree节点”怎么算呢,其实就是它自己转成二进制之后去掉最后一个1(去掉最后一个1也就是减去最后一个1所代表的数)之后的数,还是拿6来做个例子,它的二进制是110,去掉最后一个1就是100,转回来就是4了,又比如3,二进制是11,去掉最后一个1就是10,也就是2,是不是特别神奇
刚刚我们讲到了一个东西,“最后一个1”,这个东西怎么求,这里就要说到一个树状数组最重要的函数了,lowbit(),就是用来求最后一个1的,lowbit()有两种写法,都可以求最后一个1所代表的数,分别是:
(((x-1)&x)^x)
让我们把它拆开,用一个例子,看它是怎么求的:
拿1011000作例子吧
首先,x-1,使得最后的一个1变为0,末尾的连续零都变成1,1011000-0000001=1010111
然后,和x做&运算,因为末尾原本的连续0变成了连续1,而原本的最后一个1变成了0,按照与运算的规则,它们都会变成0,但是,原本的最后一个1的前面的数在x-1后都还是没有改变的,也就是说,那些位都和原本的x的每一位相同,根据与运算的规则,他们都不会变
1010111
& 1011000
____________
1010000
至此,可以发现,x唯一的变化也就是最后一个1变成了0 ,也就是只有最后一个1的那一位发生了变化,那么此时我们只需要让它与x做一次异或运算,其他位都会变成0,因为它们都一样,而最后一个1这一位就会变成1,因为它这一位不一样,这样,就可以求出最后一个1所代表的数了。
((-x)&x)
这种写法更简洁,不易记错,个人推荐这种
首先,我们要知道在计算机中的运算是使用补码的,想详细了解补码的可以看这里,于是我们可以把((-x)&x)这个运算拆开成这么几步:
1、将x的除了符号位的每一位取反
2、将得到的数+1
3、和原本的x做&运算
我们再来将每一步细细分析一下(例子自己试一下就好了哈):
1、将每一位取反之后,原本的x的最后一个1的位置变成了0,末尾的连续0变成了连续1
2、+1后末尾的连续1又变成了连续0,但是原本的x的最后一个1的位置又从0变回了1,但是其他的位都还是与原来相反
3、做完&运算之后,除了原本x的最后一个1的位置还是1之外,其他位都变成了0
lowbit()的分析至此结束
接下来我们讲一下它的用法
上面讲到了求“在它前面的高度比它大的第一个tree节点”,那么我们在了解了lowbit()这个函数之后,就可以知道,要求在x前面的高度比它大的第一个tree节点,就是tree[x-lowbit(x)]
lowbit()还有一个用法,那就是求tree[x]的父亲,x的父亲就是比x编号大且比x高度大的第一个节点,首先,比x编号大,说明它的父亲只能由x+某一个数得到,第一个节点,说明加的”某一个数“要尽可能的小,又要比x高度大,说明末尾连续零一定比x多,那么,满足要求的,就只有x+lowbit(x)了,仔细看看,是不是满足里面的每一个要求
接下来讲一下它基本的两个操作:
1、单点修改
显然的(每次看证明之类的东西时最怕看见这三个字了),若a[x]+y,那么tree[x]也一定会+y,因为每个tree节点都一定管理着相应的a点,那么当tree[x]+y,tree[x]的父亲的值也一定会+y,所以当tree[x]+y,tree[x+lowbit(x)]也要+y,同理,tree[(x+lowbit(x))+lowbit(x+lowbit(x))]也要+y(也就是x的父亲的父亲),一直加到tree的下标大于n为止(大于n的那一次不加,不然下标会越界)
2、区间查询
前面讲到了,x-lowbit(x)就是在x之前的高度比x大的第一个节点,因为tree[x]的管理范围就是x-lowbit(x)+1~x(上面有讲),所以,x-lowbit(x)那个节点和x节点的管理范围一定相邻且不重合,那么同理,(x-lowbit(x))-lowbit(x-lowbit(x))那个点(也就是x-lowbit(x)之前的高度比x-lowbit(x)大的第一个节点)的管理范围也与x-lowbit(x)节点的管理范围一定相邻且不重合,那么我们就可以得到求1~x区间和的方法,就是每一次用一个变量sum记录当前tree[x]的值,然后x-lowbit(x),然后再用sum加上tree[x-lowbit(x)],然后继续直到x=0为止,这是求1~x的方法,那么自然,求x~y就是求 1~y - 1~(x-1),那有些人就想到了,为什么不直接求x~y呢?先从y开始,每次减lowbit(y),直到y=x就停止,这样不好吗?不好。你怎么就能保证y-lowbit(y)最后能够刚好等于x呢?你总不能在y
树状数组在这两个方面的处理还是很优的,时间都只有log(n),但是,用在区间修改上呢?修改一次区间nlog(n),还没普通的数组好用,那单点查询呢?假如要你求x的值,就相当于求1~x - 1~(x-1),用时2log(n),还算不错,但是,对于区间修改,就没有更优的方法了吗?答案自然是有的,那就要用到另一个神奇的东西了,差分数组,我们只需要把树状数组用在差分数组上就可以了,因为我们知道差分数组的区间修改可以说是所有数据结构里面最快的了(O(1)的时间,实在找不出能比它快的),但是它的查询就显得很弱了,相对的,树状数组的区间修改很弱,但是查询十分的快,所以,将他们结合一下,就很厉害了,具体怎么结合呢,见下:
1、区间修改
若用差分数组做,设b为差分数组,那么每次修改只需要将b[l]+x然后b[r+1]-x即可,那么放到树状数组中,也就是只需要修改tree[l]和tree[r+1]两个点即可,那么时间就只需要2log(n)了
2、单点查询
若用差分数组做查询x的值,就是统计b数组的1~x的和,那么求前缀和这个东西树状数组是很擅长的,只需要log(n)的时间即可
但仔细看看,可以发现,这两个操作中并不会修改b数组的值,也就是说,我们并不需要真正去建一个差分数组,其实只是运用到它的思想罢了
至此,树状数组讲解完毕
树状数组2——更高深的树状数组