最小生成树原理及Kruskal算法的js实现

1. 生成树和最小生成树的概念

设图G(V,E)连通，则
生成树：包含图G(V,E)中的所有节点，及|V|-1条边的连通图，一个图的生成树可以有多颗
最小生成树：最小权重生成树，在生成树的概念上加一个限制条件，即生成树的所有边的权值总和最小的树，最小生成树也可以有多颗

2. 求解最小生成树的通用方法

由于最小生成树包含图G的所有边，所以我们需要做的只是寻找最小生成树的边集A

设：边集A是图G的任意一颗最小生成树的边的子集，初始时A为空当A不等于G的某个最小生成树的所有边集M时循环以下步骤找到一条属于M但不属于A的边，加入到A中

现在问题我们如何去寻找那条只属于M但不属于A的边

边v的寻找方法
当A为空时，图G(V,A)是一个有|V|个树的森林，当A中有n条边时，n<|V|-1,图G是一个有|V|-(n+1)个树的森林，我们需要寻找的边v的加入会导致图G中的森林数目减1边v是这样一条边

边v的两端的节点属于两颗不同的树
边v的权值是所有满足以上条件中权值最小的

3. Kruskal和Prim 算法

Kruskal和Prim 算法是最小生成树常用的两种算法，这两种算法都是对上述通用方法的细化，不同之处就是对边v的寻找方法上有所差异，Kruskal算法又叫做(边扩展)算法，适用于边稀疏的图，Prim算法叫做(节点扩展算法)，适用于边稠密的图

4. Kruskal算法

4.1. 概念
Kruskal算法的特点是上述A中的边可以属于多颗不同的树
4.2. 辅助函数 MakeSet(x)

MakeSet操作创建一个包含|V|颗树的集合，每颗树只包含一个节点，我们要为每个节点x添加两个属性

 var MakeSet = (function(){
    let set = new Set();
    return function(x) {
        x.parent = x;
        x.rank = 0;
        if(!set.has(x)) set.add(x);
        return set;
    }
})();

4.3. 辅助函数 Find(x)

找到并返回x节点所在的那颗树的根节点，用于判断两个节点是否在同一颗树中，即是否相交

 function Find(x) {
    if (x.parent != x)
        x.parent = Find(x.parent);
    return x.parent;
}

4.4. 辅助函数 Union(u, v)

Union函数旨在合并两个节点，应该将这里的合并和在图G中的连通区分开，我们通过不断调用union来改变MakeSet集合中元素的连通性，被合并的两个节点会变成一颗数,当然读者也可以实现自己的Union,随意实现都行，只有调用Union操作之后改变了MakeSet,中图的连通性，是的u，v节点处于同一颗树就行,本文的Union方法采用的思想是 按秩合并(秩 rank)、路径压缩 ，通过这种方式创建的树的节点分布,会比较均匀，平衡性较高，也就导致操作效率很高

function Union(u, v) {
    let uRoot = Find(u);
    let vRoot = Find(v);
    // 如果 u 和 v 在同一颗树
    if (uRoot == vRoot) return;
    // 如果 u 和 v 不在同一颗树中，合并它们
    // 如果 uRoot 的层级比 vRoot 的小,将 uRoot 作为 vRoot 前驱节点
    if (uRoot.rank < vRoot.rank) uRoot.parent = vRoot;
    // 如果 uRoot 的层级比 vRoot 的大,将 vRoot 作为 uRoot 前驱节点
    else if (uRoot.rank > vRoot.rank) vRoot.parent = uRoot;
    //将 uRoot 设置为根节点,并将 uRoot 的层级加一
    else {
        vRoot.parent = uRoot;
        uRoot.rank = uRoot.rank + 1;
    }
}

4.5. Kruskal算法

Kruskal算法旨在寻找最小生成数中包含哪些边,在后面的完整代码中，该函数的实现会有所不同，这里着重体会原理

function Kruskal(G, w) {
    let A = []; //A用于存放最小生成数所包含的边
    for(let x of G.V) {
        MakeSet(x);
    }
    //对G.E按照边的权中从小到大排序
    for(let e of G.E) {
        quickSort(0, G.E.length-1, G.E, 'w');
    }
    //由于边已经按照从小到大的顺序有序，所以这里只需要寻找不相交的边(边所在的树不相交)，
    for(let e of G.E) {
        if(Find(e.u)!=Find(e.v)) {
            A.push(e);
            Union(e.u, e.v); //改变连通性
        }
    }
    return A;
}

4.6. 图，顶点，边，的数据结构

这里的数据结构及如何建图参照 BFS,DFS 算法原理及js实现，这里不做详细说明

//顶点数据结构
function Vertex() {
    if (!(this instanceof Vertex))
        return new Vertex();
    this.edges = null; //由顶点发出的所有边
    this.id = null; //节点的唯一标识
    this.data = null; //存放节点的数据
}

//数据结构 邻接链表-边
function Edge() {
    if (!(this instanceof Edge))
        return new Edge();
    this.index = null; //边所依附的节点的位置
    this.sibling = null;
    this.w = null; //保存边的权值
}

//数据结构 图-G
function Graph() {
    if (!(this instanceof Graph))
        return new Graph();
    this.V = []; //节点集
    this.E = []; //边集
    this.refer = new Map(); //字典 用来映射标节点的识符和数组中的位置
}
Graph.prototype = {
    constructor: Graph,
    //这里加进来的已经具备了边的关系
    //创建图的 节点
    initVertex: function(vertexs) {
        //创建节点并初始化节点属性 id
        for (let v of vertexs) {
            let vertex = Vertex();
            vertex.id = v.id;
            this.V.push(vertex);
        }
        //初始化 字典
        for (let i in this.V) {
            this.refer.set(this.V[i].id, i);
        }
    },
    //建立图中 边 的关系
    initEdge: (function() {
        //创建链表，返回链表的第一个节点
        function createLink(index, len, edges, refer) {
            if (index >= len) return null;
            let edgeNode = Edge();
            edgeNode.index = refer.get(edges[index].id); //边连接的节点 用在数组中的位置表示 参照字典
            edgeNode.w = edges[index].w; //边的权值
            edgeNode.sibling = createLink(++index, len, edges, refer); //通过递归实现 回溯
            return edgeNode;
        }
        return function(edges) {
            for (let field in edges) {
                let index = this.refer.get(field); //从字典表中找出节点在 V 中的位置
                let vertex = this.V[index]; //获取节点
                vertex.edges = createLink(0, edges[field].length, edges[field], this.refer);
            }
        }
    }()),
    storageEdge: function(edges) {
        this.E = edges;
    }
}

var vertexs = [{id:'a'}, {id:'b'}, {id:'c'}, {id:'d'}, {id:'e'}];
var edges = [
    {u:'a',v:'b',w:3},
    {u:'a',v:'c',w:1},
    {u:'b',v:'a',w:3},
    {u:'b',v:'c',w:4},
    {u:'b',v:'d',w:5},
    {u:'c',v:'a',w:1},
    {u:'c',v:'b',w:4},
    {u:'c',v:'d',w:6},
    {u:'c',v:'e',w:7},
    {u:'d',v:'b',w:5},
    {u:'d',v:'c',w:6},
    {u:'d',v:'e',w:2},
    {u:'e',v:'c',w:7},
    {u:'e',v:'d',w:6}
]

var g = Graph();
g.initVertex(vertexs);
g.storageEdge(edges);

运行这部分代码，生成了用于Kruskal算法输入的图

4.7. 完整代码及测试

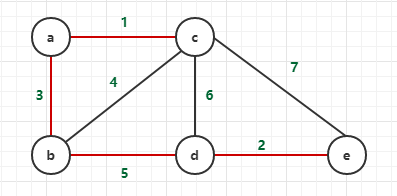
测试的算法的输入图为上图，红色的边为最终最小生成树包含的边，出现顺序依次为 ac,de,ab,bd,这里的输入图为无向图

//快速排序 数组a由对象组成 key为排序的参照指标 quickSort(0,a.length-1,a,'key')
function quickSort(left, right, a, key) {
    if (left > right)
        return;
    var i = left;
    var j = right;
    var benchMark = a[i];
    var temp;
    while (i != j) {
        //移动 j
        while (a[j][key] >= benchMark[key] && i < j)
            j--;
        //移动 i
        while (a[i][key] <= benchMark[key] && i < j)
            i++;
        if (i < j) {
            temp = a[i];
            a[i] = a[j];
            a[j] = temp;
        }
    }

    a[left] = a[i];
    a[i] = benchMark;
    quickSort(left, i - 1, a, key);
    quickSort(i + 1, right, a, key);
}

var MakeSet = (function() {
    let set = new Set();
    return function(x) {
        x.parent = x;
        x.rank = 0;
        if (!set.has(x)) set.add(x);
        return set;
    }
})();

//体会两个 Find 方法的不同
// function Find(x) {
//     if (x.parent != x)
//         Find(x.parent);
//     return x.parent;
// }

function Find(x) {
    if (x.parent != x)
        x.parent = Find(x.parent);
    return x.parent;
}

function Union(u, v) {
    let uRoot = Find(u);
    let vRoot = Find(v);
    // 如果 u 和 v 在同一颗树
    if (uRoot == vRoot) return;
    // 如果 u 和 v 不在同一颗树中，合并它们
    // 如果 uRoot 的层级比 vRoot 的小,将 uRoot 作为 vRoot 前驱节点
    if (uRoot.rank < vRoot.rank) uRoot.parent = vRoot;
    // 如果 uRoot 的层级比 vRoot 的大,将 vRoot 作为 uRoot 前驱节点
    else if (uRoot.rank > vRoot.rank) vRoot.parent = uRoot;
    //任选一个作为根节点
    else {
        vRoot.parent = uRoot;
        uRoot.rank = uRoot.rank + 1;
    }
}

function Kruskal(G) {
    let A = []; //A用于存放最小生成数所包含的边
    for(let x of G.V) {
        MakeSet(x);
    }
    //对G.E按照边的权中从小到大排序
    for(let e of G.E) {
        quickSort(0, G.E.length-1, G.E, 'w');
    }
    for(let e of G.E) {
        let u = G.V[G.refer.get(e.u)];
        let v = G.V[G.refer.get(e.v)];
        if(Find(u)!=Find(v)) {
            A.push(e);
            Union(u, v);
        }
    }
    return A;
}

function Vertex() {
    if (!(this instanceof Vertex))
        return new Vertex();
    this.edges = null; //由顶点发出的所有边
    this.id = null; //节点的唯一标识
    this.data = null; //存放节点的数据
}

//数据结构 邻接链表-边
function Edge() {
    if (!(this instanceof Edge))
        return new Edge();
    this.index = null; //边所依附的节点的位置
    this.sibling = null;
    this.w = null; //保存边的权值
}

//数据结构 图-G
function Graph() {
    if (!(this instanceof Graph))
        return new Graph();
    this.V = []; //节点集
    this.E = [];
    this.refer = new Map(); //字典 用来映射标节点的识符和数组中的位置
}
Graph.prototype = {
    constructor: Graph,
    //这里加进来的已经具备了边的关系
    //创建图的 节点
    initVertex: function(vertexs) {
        //创建节点并初始化节点属性 id
        for (let v of vertexs) {
            let vertex = Vertex();
            vertex.id = v.id;
            this.V.push(vertex);
        }
        //初始化 字典
        for (let i in this.V) {
            this.refer.set(this.V[i].id, i);
        }
    },
    //建立图中 边 的关系
    initEdge: (function() {
        //创建链表，返回链表的第一个节点
        function createLink(index, len, edges, refer) {
            if (index >= len) return null;
            let edgeNode = Edge();
            edgeNode.index = refer.get(edges[index].id); //边连接的节点 用在数组中的位置表示 参照字典
            edgeNode.w = edges[index].w; //边的权值
            edgeNode.sibling = createLink(++index, len, edges, refer); //通过递归实现 回溯
            return edgeNode;
        }
        return function(edges) {
            for (let field in edges) {
                let index = this.refer.get(field); //从字典表中找出节点在 V 中的位置
                let vertex = this.V[index]; //获取节点
                vertex.edges = createLink(0, edges[field].length, edges[field], this.refer);
            }
        }
    }()),
    storageEdge: function(edges) {
        this.E = edges;
    }
}

//测试数据
var vertexs = [{id:'a'}, {id:'b'}, {id:'c'}, {id:'d'}, {id:'e'}];
var edges = [
    {u:'a',v:'b',w:3},
    {u:'a',v:'c',w:1},
    {u:'b',v:'a',w:3},
    {u:'b',v:'c',w:4},
    {u:'b',v:'d',w:5},
    {u:'c',v:'a',w:1},
    {u:'c',v:'b',w:4},
    {u:'c',v:'d',w:6},
    {u:'c',v:'e',w:7},
    {u:'d',v:'b',w:5},
    {u:'d',v:'c',w:6},
    {u:'d',v:'e',w:2},
    {u:'e',v:'c',w:7},
    {u:'e',v:'d',w:6}
]

var g = Graph();
g.initVertex(vertexs);
g.storageEdge(edges);
var A = Kruskal(g);
console.log(A);

最小生成树原理及Kruskal算法的js实现

1. 生成树和最小生成树的概念

2. 求解最小生成树的通用方法

3. Kruskal和Prim 算法

4. Kruskal算法

你可能感兴趣的:(node.js,javascript,最小生成树,算法)