leetcode股票买卖题目汇总

Best Time to Buy and Sell Stock

允许一次买卖

思路：O(n)时间复杂度，非常简单

class Solution {
public:
    int maxDiff(vector& nums) {
        if(nums.size() < 2) return 0;
        int max_profit = 0,profit = 0;
        for(int i = 1;i < nums.size();i++){
            if(profit < 0) profit = 0;
            profit += (nums[i]-nums[i-1]);
            max_profit = max(max_profit,profit);
        }
        return max_profit;
    }
};

 

Best Time to Buy and Sell Stock II 

允许多次买卖

思路：O(n)时间，当前比前一个有增加，加上收益即可

class Solution {
public:
    int maxProfit(vector& prices) {
        int profit = 0;
        for(int i = 1;i < prices.size();i++){
            if(prices[i]-prices[i-1] > 0){
                profit += prices[i]-prices[i-1];
            } 
        }
        return profit;
    }
};

 

 

Best Time to Buy and Sell Stock with Transaction Fee

每次卖出有手续费

参考：https://www.cnblogs.com/grandyang/p/7776979.html

这道题有了交易费，所以当卖出的利润小于交易费的时候，我们就不应该卖了，不然亏了。所以这道题还是还是得用动态规划来做，本质其实是个三维dp数组，由于第三维只有两种情况，卖出和保留，而且第二维交易的次数在这道题中没有限制，所以我们用两个一维数组就可以了

sold[i]表示第i天卖掉股票此时的最大利润

hold[i]表示第i天保留手里的股票此时的最大利润

那么我们来分析递推公式，在第i天，如果我们要卖掉手中的股票，那么此时我们的总利润应该是前一天手里有股票的利润(不然没股票卖毛啊)，加上此时的卖出价格，减去交易费得到的利润总值，跟前一天卖出的利润相比，取其中较大值，如果前一天卖出的利润较大，那么我们就前一天卖了，不留到今天了。然后来看如果第i天不卖的利润，就是昨天股票卖了的利润然后今天再买入股票，得减去今天的价格，得到的值和昨天股票保留时的利润相比，取其中的较大值，如果昨天保留股票的利润大，那么我们就继续保留到今天，所以递推时可以得到：

sold[i] = max(sold[i - 1], hold[i - 1] + prices[i] - fee);

hold[i] = max(hold[i - 1], sold[i - 1] - prices[i]);

class Solution {
public:
    int maxProfit(vector& prices, int fee) {
        if(prices.size() < 2) return 0;
    
        int sold = 0,hold = -prices[0];
        for(int i = 1;i < prices.size();i++){
            int last_sold = sold;
            // 本次手上是已卖出的
            sold = max(sold,hold+prices[i]-fee);
            // 本次手上是有股票的
            hold = max(hold,last_sold-prices[i]);
        }
        return sold;
    }
};

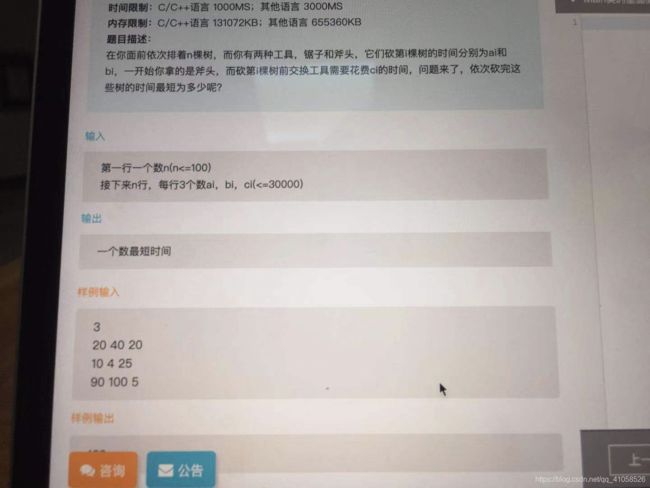
思路一样的题：

import sys

def mintime(A,B,C):
    // i步用的是锯子，所花的最少时间
    cur_a = A[0]+C[0]
    // i步用的是斧子，所花的最少时间
    cur_b = B[0]
    for i in range(1,len(A)):
        cur_a = min(cur_a+A[i],cur_b+A[i]+C[i])
        cur_b = min(cur_b+B[i],cur_a+B[i]+C[i])
    return min(cur_a,cur_b)


if __name__ == "__main__":
    input_lines = []
    n = int(sys.stdin.readline().strip())
    A = []
    B = []
    C = []
    for i in range(n):
        a,b,c = map(int,input().split())
        A.append(a)
        B.append(b)
        C.append(c)

    res = mintime(A,B,C)
    print(res)

 

 

Best Time to Buy and Sell Stock III

只能交易两次

思路：

这道题是一道动态规划题，时间复杂度O(2N)

（1）global[i][j]：当前到达第 i 天，可以最多进行 j 次交易（不一定一定要交易到 j 次），最好的利润是多少

global[i][j] = max(local[i][j], global[i - 1][j])

取当前局部最好的，和过往全局最好的中大的那个（因为最后一次交易如果包含当前天一定在局部最好的里面，否则一定在过往全局最优的里面）

（2）local[i][j]：当前到达第 i 天，最多可进行 j 次交易，并且最后一次交易在当天卖出的最好的利润是多少

它们的递推式为：

local[i][j] = max(global[i - 1][j - 1] + max(diff, 0), local[i - 1][j] + diff)

第一个是全局到i-1天进行j-1次交易，然后加上今天的交易，如果今天是赚钱的话（也就是前面只要j-1次交易，最后一次交易取当前天），如果今天不赚钱，就让其今天买进再卖出，这样也增加了一次交易，最后一次交易也在今天

第二个量则是取local第i-1天j次交易，然后加上今天的差值（这里因为local[i-1][j]比如包含第i-1天卖出的交易，所以现在变成第i天卖出，并不会增加交易次数，而且这里无论diff是不是大于0都一定要加上，因为否则就不满足local[i][j]必须在最后一天卖出的条件了）。
 

class Solution {
public:
    int maxProfit(vector& prices) {
        if(prices.empty()) return 0;
        int n = prices.size();
        // 注意这里是3，否则下面出现j-1的时候会有问题，这里让j=1的时候，j-1的值为0
        int local[n][3] = {0};
        int global[n][3] = {0};
        for(int i = 1;i < n;i++){
            int diff = prices[i]-prices[i-1];
            for(int j = 1;j <= 2;j++){
                local[i][j] = max(local[i-1][j]+diff,global[i-1][j-1]+max(0,diff));
                global[i][j] = max(global[i-1][j],local[i][j]);
            }
        }
        return global[n-1][2];
    }
};

 

 

Best Time to Buy and Sell Stock with Cooldown

有冷却时间

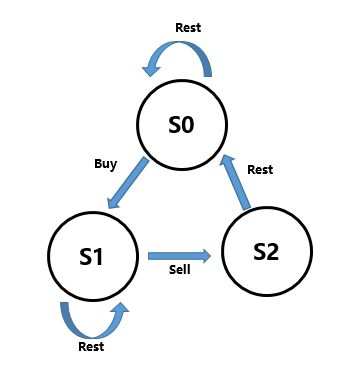
这道题可以用动态规划的思路解决。但是一开始想的时候总是抽象不出状态转移方程来，之后看到了一种用状态机的思路，觉得很清晰，特此拿来分享，先看如下状态转移图

s0表示在第i天之前最后一个操作是冷冻期（此时既可以继续休息，又可以开始买入），此时的最大收益。

s1表示在第i天之前最后一个操作是买（此时可以卖出，可以休息），此时的最大收益。

s2表示在第i天之前最后一个操作是卖（此时只能休息），此时的最大收益。

这里我们把状态分成了三个，根据每个状态的指向，我们可以得出下面的状态转移方程：

s0[i] = max(s0[i-1], s2[i-1])
s1[i] = max(s1[i-1], s0[i-1] - price[i])
s2[i] = s1[i-1] + price[i]
 

class Solution {
public:
    int maxProfit(vector& prices) {
        int n = prices.size();
        if(n < 2) return 0;
        vector s0(n);
        vector s1(n);
        vector s2(n);
        s0[0] = 0;
        s1[0] = -prices[0];
        // 注意这里不能定义为0
        s2[0] = INT_MIN;
        for(int i = 1;i < n;i++){
            s0[i] = max(s0[i-1],s2[i-1]);
            s1[i] = max(s0[i-1]-prices[i],s1[i-1]);
            s2[i] = s1[i-1]+prices[i];
        }
        return max(s0[n-1],s2[n-1]);
    }
};