数据结构和算法(十)冒泡排序
文章目录
- 定义
- 算法步骤
- 动图分析
- 过程分析
- python实现冒泡排序
- 冒泡排序第一次优化
- 冒泡排序第二次优化
- 冒泡排序的变形——鸡尾酒排序
- 时间复杂度
- 稳定性
定义
冒泡排序是一种简单的排序算法。它重复地遍历要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。遍历数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
算法步骤
- 比较相邻的两个元素,如果第一个比第二个大,则交换它们两个。
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
- 针对所有的元素重复以上的步骤,除了最后一个。
- 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
动图分析
过程分析
这六个数组成的无序序列[5,9,3,6,2,7],由小到大排序。
按照冒泡排序算法,相邻元素两两比较,过程如下:
- 首先比较5和9,5比9小,所以元素位置不变:第一次交换结果为 [5, 9, 3, 6, 2, 7]
- 继续比较9和3,9比3大,所以互换位置:第二次交换结果为 [5, 3, 9, 6, 2, 7]
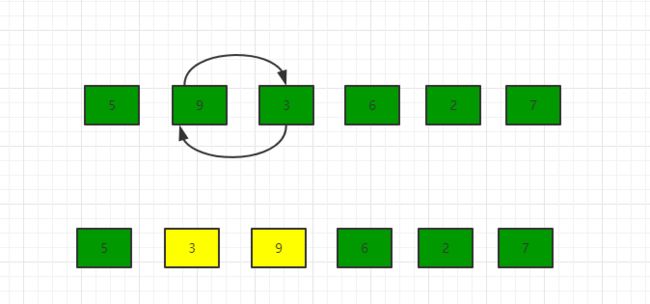
- 继续比较9和6,9比6大,所以互换位置:第三次交换结果为[5, 3, 6, 9, 2, 7]
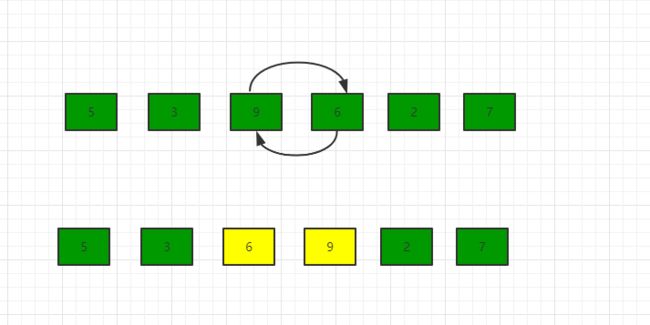
- 继续比较9和2,9比2大,所以互换位置,第四次交换结果为[5, 3, 6, 2, 9, 7]

- 继续比较9和7,9比7大,所以互换位置,第五次交换结果为[5, 3, 6, 2, 7, 9]

这样一来 最大元素9像气泡一样,飘到了最右面。
这时候,我们的冒泡排序的第一轮结束了。数列最右侧的元素9可以认为是一个有序区域,有序区域目前只有一个元素。

下面进行第二轮冒泡排序 - 首先比较5和3,5比3大,所以互换位置,第二轮第一次交换结果为[3, 5, 6, 2, 7, 9]
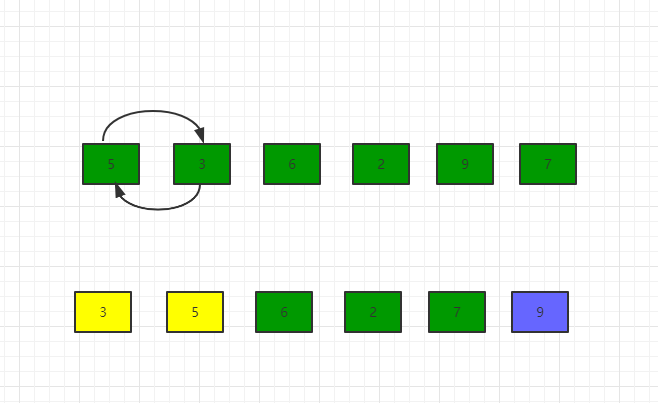
- 继续比较5和6,5比6小,所以元素位置不变,第二轮第二次交换结果为[3, 5, 6, 2, 7, 9]
- 继续比较6和2,6比2大,所以互换位置,第二轮第三次交换结果为[3, 5, 2, 6, 7, 9]
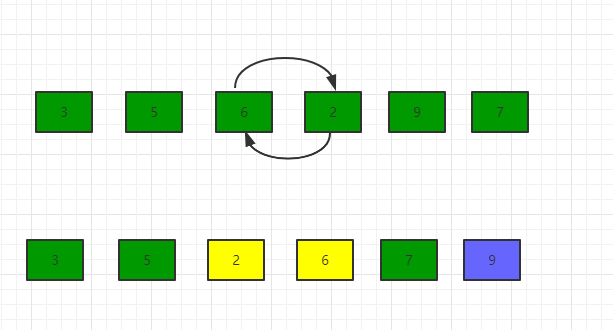
- 继续比较6和7,6比7小,所以元素位置不变,第二轮第四次交换结果为[3, 5, 2, 6, 7, 9]
这样一来,经过两轮排序,右侧有序序列变成了两个元素。

后续交换细节如上,所以第三轮交换结果为[3, 2, 5, 6, 7, 9]

第四轮交换结果为[2, 3, 5, 6, 7, 9]
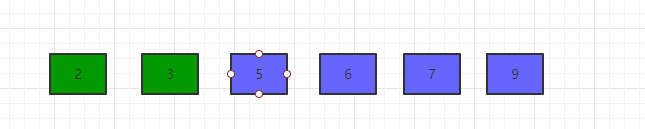
第五轮交换结果为[2, 3, 5, 6, 7, 9]
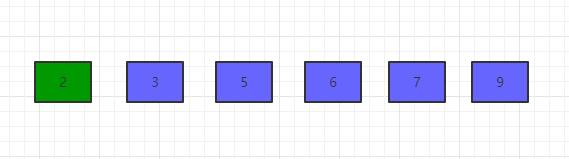
到此为止,元素变成有序的了,这就是冒泡排序的整体思路。
python实现冒泡排序
def bubble_sort(arr):
loop_count = 0
for j in range(len(arr) - 1):
for i in range(len(arr) - 1 - j):
loop_count += 1
if arr[i] > arr[i+1]:
arr[i], arr[i+1] = arr[i+1], arr[i]
print("第{}趟的第{}次交换的结果:{}".format(j+1, i+1, arr))
print("第{}趟的结果:{}".format(j+1, arr))
print("*"*20)
print("循环次数为:{}".format(loop_count))
return arr
if __name__ == '__main__':
arr = [5,9,3,6,2,7]
print(bubble_sort(arr))
结果
第1趟的第1次交换的结果:[5, 9, 3, 6, 2, 7]
第1趟的第2次交换的结果:[5, 3, 9, 6, 2, 7]
第1趟的第3次交换的结果:[5, 3, 6, 9, 2, 7]
第1趟的第4次交换的结果:[5, 3, 6, 2, 9, 7]
第1趟的第5次交换的结果:[5, 3, 6, 2, 7, 9]
第1趟的结果:[5, 3, 6, 2, 7, 9]
********************
第2趟的第1次交换的结果:[3, 5, 6, 2, 7, 9]
第2趟的第2次交换的结果:[3, 5, 6, 2, 7, 9]
第2趟的第3次交换的结果:[3, 5, 2, 6, 7, 9]
第2趟的第4次交换的结果:[3, 5, 2, 6, 7, 9]
第2趟的结果:[3, 5, 2, 6, 7, 9]
********************
第3趟的第1次交换的结果:[3, 5, 2, 6, 7, 9]
第3趟的第2次交换的结果:[3, 2, 5, 6, 7, 9]
第3趟的第3次交换的结果:[3, 2, 5, 6, 7, 9]
第3趟的结果:[3, 2, 5, 6, 7, 9]
********************
第4趟的第1次交换的结果:[2, 3, 5, 6, 7, 9]
第4趟的第2次交换的结果:[2, 3, 5, 6, 7, 9]
第4趟的结果:[2, 3, 5, 6, 7, 9]
********************
第5趟的第1次交换的结果:[2, 3, 5, 6, 7, 9]
第5趟的结果:[2, 3, 5, 6, 7, 9]
********************
循环次数为:15
[2, 3, 5, 6, 7, 9]
冒泡排序第一次优化
上面可以看出,第四轮之后序列就会变成有序的了,但是程序还会继续执行下去。对于这种情况如果我们能判断出数列已经有序,并且做出标记,剩下的几轮排序就可以不必执行,提早结束工作。
def bubble_sort(arr):
for j in range(len(arr) - 1):
# 标记,判断元素是否需要交换,默认有序 设为True
is_sort = True
for i in range(len(arr) - 1 - j):
if arr[i] > arr[i+1]:
arr[i], arr[i+1] = arr[i+1], arr[i]
# 有交换 说明无序 设为False
is_sort = False
# 如果有序 跳出循环
if is_sort:
break
return arr
if __name__ == '__main__':
arr = [5,9,3,6,2,7]
print(bubble_sort(arr))
冒泡排序第二次优化
为了说明问题,使用一个新序列[3,4,2,1,5,6,7,8]
按照冒泡排序过程 第一轮结果为[3,2,1,4,5,6,7,8],我们发现后面 4,5,6,7,8已经有序了,按照常规冒泡,还会依次比较有序的序列,每一轮做很多无用功。
这种情况的关键点在于有序和无序区的界线。
按照现有的逻辑,有序区的长度和排序的轮数是相等的。比如第一轮排序过后的有序区长度是1,第二轮排序过后的有序区长度是2 ……
实际上,数列真正的有序区可能会大于这个长度,比如例子中仅仅第二轮,后面5个元素实际都已经属于有序区。因此后面的许多次元素比较是没有意义的。
如何避免这种情况呢?我们可以在每一轮排序的最后,记录下最后一次元素交换的位置,那个位置也就是无序数列的边界,再往后就是有序区了。循环只循环到临界点,减少了循环次数,达到优化目的。
代码实现
def bubble_sort(arr):
loop_count = 0
# 最后一个交换的位置
last_change_index = 0
# 有序和无序的分界线
sort_border = len(arr) - 1
for j in range(len(arr) - 1):
# 标记,判断元素是否需要交换,默认有序 设为True
is_sort = True
for i in range(sort_border):
loop_count += 1
if arr[i] > arr[i+1]:
arr[i], arr[i+1] = arr[i+1], arr[i]
# 有交换 说明无序 设为False
is_sort = False
last_change_index = i
# 如果有序 跳出循环
if is_sort:
break
# 最后一个交换的位置就是边界
sort_border = last_change_index
print("循环次数为:{}".format(loop_count))
return arr
if __name__ == '__main__':
arr = [5,9,3,6,2,7]
print(bubble_sort(arr))
结果
循环次数为:12
[2, 3, 5, 6, 7, 9]
冒泡排序的变形——鸡尾酒排序
至于为什么叫鸡尾酒排序,我也没太理解,看一下维基百科说的吧
通俗理解就是双向冒泡排序,就是它可以从两个方向进行排序,第一次从左到右,第二次从右到左,第三次再从左到右…,像钟摆一样,来回摆动。
代码实现
# 简版
def bubble_sort(arr):
for j in range(len(arr) - 1):
# 标记,判断元素是否需要交换,默认有序 设为True
is_sort = True
for i in range(len(arr) - 1 - j):
if arr[i] > arr[i+1]:
arr[i], arr[i+1] = arr[i+1], arr[i]
# 有交换 说明无序 设为False
is_sort = False
# 如果有序 跳出循环
if is_sort:
break
is_sort = True
for k in range(len(arr) - 1-j, 0, -1):
if arr[k] < arr[k-1]:
arr[k], arr[k-1] = arr[k-1], arr[k]
# 有交换 说明无序 设为False
is_sort = False
# 如果有序 跳出循环
if is_sort:
break
return arr
# 优化版
def bubble_sort(arr):
# 记录右侧最后一个交换的位置
right_last_change_index = 0
# 右侧有序和无序的分界线
right_sort_border = len(arr) - 1
# 记录左侧最后一个交换的位置
left_last_change_index = 0
# 左侧有序和无序的分界线
left_sort_border = 0
for j in range(len(arr) - 1):
# 标记,判断元素是否需要交换,默认有序 设为True
is_sort = True
for i in range(right_sort_border):
if arr[i] > arr[i+1]:
arr[i], arr[i+1] = arr[i+1], arr[i]
# 有交换 说明无序 设为False
is_sort = False
right_last_change_index = i
# 如果有序 跳出循环
if is_sort:
break
# 最后一个交换的位置就是边界
right_sort_border = right_last_change_index
is_sort = True
for k in range(right_sort_border, left_sort_border, -1):
if arr[k] < arr[k-1]:
arr[k], arr[k-1] = arr[k-1], arr[k]
# 有交换 说明无序 设为False
is_sort = False
left_last_change_index = k
# 如果有序 跳出循环
if is_sort:
break
# 最后一个交换的位置就是边界
left_sort_border = left_last_change_index
return arr
鸡尾酒排序等于是冒泡排序的轻微变形。不同的地方在于从低到高然后从高到低,而冒泡排序则仅从低到高去比较序列里的每个元素。他可以得到比冒泡排序稍微好一点的性能,原因是冒泡排序只从一个方向进行比对(由低到高),每次循环只移动一个项目。
以序列(2,3,4,5,1)为例,鸡尾酒排序只需要访问一次序列就可以完成排序,但如果使用冒泡排序则需要四次。但是在随机数序列的状态下,鸡尾酒排序与冒泡排序的效率与其他众多排序算法相比均比较低。
鸡尾酒排序最糟或是平均所花费的次数都是o(n^2),但如果序列在一开始已经大部分排序过的话,会接近O(n)。
时间复杂度
- 最坏时间复杂度O(n^2)
- 最优时间复杂度O(n) (表示遍历一次发现没有任何可以交换的元素,排序结束。)
稳定性
什么是稳定性?
稳定性就是会让原本有相等键值的纪录维持相对次序。也就是如果一个排序算法是稳定的,当有两个相等键值的纪录R和S,且在原本的列表中R出现在S之前,在排序过的列表中R也将会是在S之前。
比如有一个序列 5,2,3,3,4,1。第一个3暂且叫3’,第二个3叫3",经过稳定排序算法为:5,2,3’,3",4,1,两个3的相对位置没有改变。不稳定排序算法为:5,2,3",3’,4,1
冒泡排序算法是稳定的。