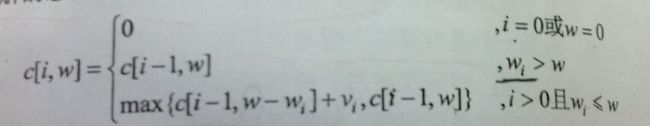动态规划算法解决0-1背包问题

一．基本概念

　　动态规划算法与分治法类似，其七本思想也是将待求解的问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。与分治法不同的是，适合用动态规划法求解的问题，经分解得到的子问题往往不是独立的。动态规划算法用一个表来记录所有已解决问题子问题的答案，在需要的时候再找出已求得的答案。

适合用动态规划算法求解的问题。

二.　基本思想与策略

　　动态规划算法，通常用于求解具有某种最优性质的问题。在这类问题中，可能会有许多可行解，每一个解对应一个值，我们希望找到具有最优值（最大值或最小值）的那个解。当然最优解可能有多个。动态规划算法能找出其中的一个最优解。

三. 　适用的情况

1. 最优子结构：如果一个问题的最优解中包含了其中子问题的最优解。就说该问题具有最优子结构。当一个问题具有最优子结构是，提示我们动态规划法可能会适用，但是此时贪心策略可能也是适用的。　　　　　　　　

 

1. 重叠子问题。重叠子问题指用来解原问题的递归算法可反复地解同样的子问题，而不是总在产生新的子问题。即当一个递归算法不断地调用同一个问题时，就说该问题包含重叠子问题。此时若用分治法递归求解，则每次遇到子问题都会视为新问题，会极大地降低算法的效率，而动态规划法总是充分利用重叠子问题，对每个子问题计算一次，把解保存在一个需要时就可以查看的表中，而每次查表的时间为常数。

四.      以0-1背包问题规划求解过程。

 

 

表一，物品的价值和重量

物品编号	1	2	3	4	5
价值v	4	5	10	11	13
重量w	3	4	7	8	9

 

递归定义最优解的值

 

动态规划的核心思想是：随着背包容量的增大，可放入背包的物品的个数越多，最优解也会不同。

 

表二，随着背包容量的增大，物品可放可不放

（0代表此物品在当前背包容量下，不可放入背包，1代表此物品在当前背包容量下，可以放入背包）

 

	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
1	0	0	0	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
2	0	0	0	0	1	1	1	1	1	1	1	1	1	1	1	1	1	1
3	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1	1	1	1
4	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1	1	1
5	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1	1

 

 

表三，最优值（在当前物品编号下，求得的最优解）

	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
1	0	0	0	4	4	4	4	4	4	4	4	4	4	4	4	4	4	4
2	0	0	0	4	5	5	5	9	9	9	9	9	9	9	9	9	9	9
3	0	0	0	4	5	5	5	10	10	10	14	15	15	15	19	19	19	19
4	0	0	0	4	5	5	5	10	11	11	14	15	16	16	19	21	21	21
5	0	0	0	4	5	5	5	10	11	13	14	15	17	18	19	21	23	24

 

 

以下是用递归算法推导的过程

背包容量为3，5个物品中可供选择的物品为1个

c[5,3]=c[4,3]=c[3,3]=c[2,3]=c[1,3]=4

 

 

背包容量为4，,5个物品中可供选择的物品为2个

c[5,4]=c[4,4]=c[3,4]=c[2,4]=max{c[1,0]+v2,c[1,4]}=max{5,4}=5

   c[1,4]=4

背包容量为7，5个物品中可供选择的物品为3个

c[5,7]=c[4,7]=c[3,7]=max{c[2,0]+v3,c[2,7]}=max{10,c[2,7]}=max{10,9}=10

  c[2,7]=max{c[1,3]+v2,c[1,7]}=max{4+5,4}=9

      c[1,7]=4

 

背包容量为8，5个物品中可供选择的物品为4个

c[5,8]=c[4,8]=max{c[3,0]+v4,c[3,8]}=max{11,c[3,8]}=max{11,10}=11

 c[3,8]=max{c[2,1]+v3,c[2,8]}=max{10,c[2,8]}=max{10,9}=10

     c[2,8]=max{c[1,4]+v2,c[1,8]}=max{4+5,c[1,8]}=c[9,4]=9

c[1,8]=4

背包容量为9，5个物品中可供选择的物品为5个

c[5,9]=max{c[4,0]+v5,c[4,9]}=max{13,c[4,9]}=max{13,11}=13

     c[4,9]=max{c[3,1]+v4,c[3,9]}=max{c[3,1]+11,c[3,9]}=max{11,c[3,19]}=max{11,10}=11

c[3,9]=max{c[2,2]+10,c[2,9]}=max{10,c[2,9]}=max{10,9}=10

     c[2,9]=max{c[1,4]+v2,c[1,9]}=max{4+5,4}=9

c[1,9]=4

背包容量为10,5个物品中可供选择的物品有5个

c[5,10]=max{c[4,1]+v5,c[4,10]}=max{c[4,1]+13,c[4,10]}=max{13,c[4,10]}=max{13,14}=14

     c[4,10]=max{c[3,2]+v4,c[3,10]}=max{11,c[3,10]}={11,14}=14

          c[3,10]=max{c[2,3]+v3,c[2,10]}=max{4+10,c[2,10]}=max{14,9}=14

    c[2,10]=max{c[1,6]+v2,c[1,10]}=max{4+5,4}=9

c[1,10]=4

 

背包容量为11,5个物品中可供选择的物品有5个

 

c[5,11]=max{c[4,2]+v5,c[4,11]}=max{13,c[4,11]}=max{13,15}=15

     c[4,11]=max{c[3,3]+v4,c[3,11]}=max{c[3,3]+11,c[3,11]}=max{15,15}=15

c[3,11]=max{c[2,4]+v3,c[2,11]}=max{c[2,4]+10,c[2,11]}=max{15,9}=15

     c[2,11]=max{c[1,8]+v2,c[1,11]}=max{c[1,8]+5,c[1,11]}=max{9,4}=9

c[1,11]=max{c[0,8]+v1,c[0,11]}=max{4,0}=4

 

 

背包容量为12,5个物品中可供选择的物品有5个

c[5,12]=max{c[4,3]+v5,c[4,12]}=max{c[4,3]+13,c[4,12]}=max{17,16}=17

     c[4,12]=max{c[3,4]+v4,c[3,12]}=max{c[3,4]+11,c[3,12]}=max{16,15}=16

          c[3,12]=max{c[2,5]+v3,c[2,12]}=max{c[2,5]+10,c[2,12]}=max{15,9}=15

     c[2,12]=max{c[1,8]+v2,c[1,12]}=max{9,4}=9

          c[1,12]=max{c[0,8]+v1,c[0,12]}=max{4,0}=4

 

 

背包容量为13,5个物品中可供选择的物品有5个

c[5,13]=max{c[4,4]+v5,c[4,13]}=max{c[4,4]+13,c[4,13]}=max{18,16}=18

     c[4,13]=max{c[3,5]+v4,c[3,13]}=max{c[3,5]+11,c[3,13]}=max{16,15}=16

          c[3,13]=max{c[2,6]+v3,c[2,13]}=max{c[2,6]+10,c[2,13]}=max{15,9}=15

     c[2,13]=max{c[1,9]+v2,c[1,13]}=max{c[1,9]+5,c[1,13]}=max{9,4}=9

         c[1,13]=max{c[0,10]+v1,c[0,13]}=max{4,0}=4

 

 

背包容量为14,5个物品中可供选择的物品有5个

c[5,14]=max{c[4,5]+v5,c[4,14]}=max{c[4,5]+13,c[4,14]}=max{18,19}=19

     c[4,14]=max{c[3,6]+v4,c[3,14]}=max{c[3,6]+11,c[3,14]}=max{16,19}=19

          c[3,14]=max{c[2,7]+v3,c[2,14]}=max{c[2,7]+10,c[2,14]}=max{19,9}=19

     c[2,14]=max{c[1,10]+v2,c[1,14]}=max{c[1,10]+5,c[1,14]}=max{9,4}=9

         c[1,14]=max{c[0,11]+v1,c[0,14]}=max{4,0}=4

     c[0,14]=0

 

背包容量为15,5个物品中可供选择的物品有5个

c[5,15]=max{c[4,6]+v5,c[4,15]}=max{c[4,6]+13,c[4,15]}=max{18,21}=21

     c[4,15]=max{c[3,7]+v4,c[3,15]}=max{c[3,7]+11,c[3,15]}=max{21,19}=21          c[3,15]=max{c[2,8]+v3,c[2,15]}=max{c[2,8]+10,c[2,15]}=max{19,9}=19

     c[2,15]=max{c[1,11]+v2,c[1,15]}=max{9,4}=9

         c[1,15]=max{c[0,12]+v1,c[0,15]}=max{4,0}=4

     c[0,15]=0

 

背包容量为16,5个物品中可供选择的物品有5个

 

c[5,16]=max{c[4,7]+v5,c[4,16]}=max{c[4,7]+v5,c[4,16]}=max{c[4,7]+13,c[4,12]}=max{23,21}=23     c[4,16]=max{c[3,8]+v4,c[3,16]}=max{c[3,8]+11,c[3,16]}=max{21,19}=21

          c[3,16]=max{c[2,9]+v3,c[2,16]}=max{c[2,9]+10,c[2,16]}=max{19,9}=19

     c[2,16]=max{c[1,12]+v2,c[1,16]}=max{9,4}=9

         c[1,16]=max{c[0,13]+v1,c[0,16]}=max{4,0}=4

 

背包容量为17,5个物品中可供选择的物品有5个

 

c[5,17]=max{c[4,9]+v5,c[4,17]}=max{c[4,9]+13,c[4,17]}=max{24,16}=24

     c[4,17]=max{c[3,9]+v4,c[3,17]}=max{c[3,9]+11,c[3,17]}=max{21,19}=21

         c[3,17]=max{c[2,10]+v3,c[2,17]}=max{c[2,10]+10,c[2,17]}=max{19,9}=19

     c[2,17]=max{c[1,13]+v2,c[1,17]}=max{9,4}=9

         c[1,17]=max{c[0,14]+v1,c[0,17]}=max{4,0}=4

 

 

 

 

表四，最优解(1表示物品在其中，0表示物品不在其中)

最优解的推导过程。

 

c[5,17]

我们如何判断哪个物品在背包中，哪个物品不在背包中，

求c[5,17]的最优解

判断第5个物品是否在背包中:判断c[5,17]与c[5,17]是否相等，24>21,第5个物品在背包中。

(第5个物品在背包中，背包现有容量为17-9=8)

判断第4个物品时否在背包中：判断c[4,8]与c[3,8]是否相等，11>10,第4个物品在背包中。

(第5个物品在背包中，背包现有容量为8-7=1)

 

最优解为 (0,0,0,1,1)

 

同理，求c[5,16]

判断第5个物品是否在背包中:判断c[5,16]与c[4,16-w5]是否相等，23>21,第5个物品在背包中。

判断第4个物品时否在背包中：背包剩余容量74,所以物品4不在背包中，

判断第3个物品是否在背包中：c[3,7]与c[2,0]是否相等，判断c[4,7]与c[3,7-w4]是否相等，10>0,第3个物品在背包中。

最优解为(0,0,1,0,1)

 

同理，求c[5,15]

判断第5个物品是否在背包中:  判断c[5,15]与c[4,15]是否相等，21>21,第5个物品不在背包中。

判断第4个物品时否在背包中：判断c[4,15]与c[3,15]是否相等，19<21,第4个物品，在背包中，

判断第3个物品是否在背包中：判断c[3,7]与c[2,7]是否相等，10>9,第3个物品在背包中，背包剩余容量为0

最优解为(0,0,1,1,0)

 

同理，求c[5,14]

判断第5个物品是否在背包中:判断c[5,14]与c[4,14]是否相等，19=19,第5个物品不在背包中。

判断第4个物品时否在背包中：判断c[4,14]与c[3,14]是否相等，19=19,第4个物品不在背包中。

判断第3个物品是否在背包中：判断c[3,14]与c[2,14]是否相等，15>9,第3个物品在背包中。

判断第2个物品是否在背包中：判断c[2,7]与c[1,7]是否相等，9>4,第2个物品在背包中。

判断第1个物品是否在背包中：判断c[1,3]是否为0,4>0,第1个物品在背包中。

最优解为(1,1,1,0,0)

 

 

同理，求c[5,13]

判断第5个物品是否在背包中:判断c[5,13]与c[4,13]是否相等，18>16,第5个物品在背包中。

背包剩余容量为4，物品4，物品3，均无法放入背包。

 

判断第2个物品时否在背包中:判断c[2,4]与c[1,4]是否相等，5>4,第2个物品在背包中。

最优解为(0,1,0,0,1)

 

 

同理，求c[5,12]

判断第5个物品是否在背包中:判断c[5,12]与c[4,12]是否相等，17>16,第5个物品在背包中。

背包剩余容量为3，物品4,3,2，均无法放入背包

判断第1个物品时否在背包中:判断c[1,3]与0是否相等，4>0,第1个物品在背包中。

最优解为(1,0,0,0,1)

 

　　综上是用动态规划算法解决0-1背包问题，并求得最优解的过程。课本中的动态规划讲述的是递归思想，但是给出的代码却是用递推方式实现的。用递推的方式更好地体现了动态的概念，背包的容量一开始并不是就将背包的容量设为17，而是物品的重量是动态变化的，我们先算出背包容量较小时，背包容量的最大价值，然后随着背包容量的增加，我们再来计算此时背包容量的最大价值，此时的最优解，需要之前的背包容量较小时的最优解，递推的实现方式，比递归地实现方式简单一些。“递归地思想，递推的实现”。