常见面试的查找和排序算法
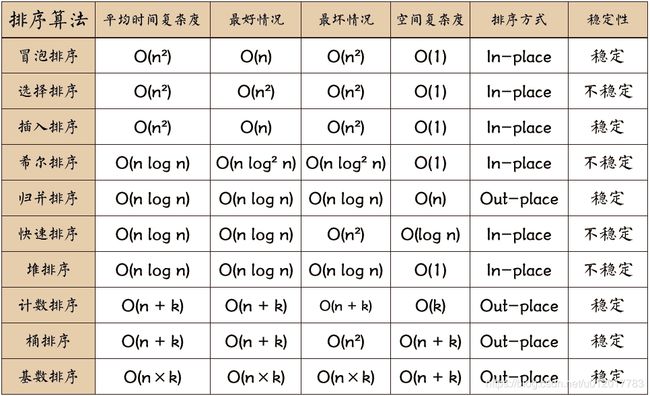
一、排序总结
(1) 快排
private void quicksort(int[] array, int begin, int end) {
// TODO Auto-generated method stub
if(beginkey)
{
j--;
}
if(i (2) 堆排序
public static void heapSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
for (int i = 0; i < arr.length; i++) {
heapInsert(arr, i);
}
int size = arr.length;
swap(arr, 0, --size);
while (size > 0) {
heapify(arr, 0, size);
swap(arr, 0, --size);
}
}
//建堆
public static void heapInsert(int[] arr, int index) {
while (arr[index] > arr[(index - 1) / 2]) {
swap(arr, index, (index - 1) / 2);
index = (index - 1) / 2;
}
}
//堆调整
public static void heapify(int[] arr, int index, int size) {
int left = index * 2 + 1;
while (left < size) {
int largest = left + 1 < size && arr[left + 1] > arr[left] ? left + 1 : left;
largest = arr[largest] > arr[index] ? largest : index;
if (largest == index) {
break;
}
swap(arr, largest, index);
index = largest;
left = index * 2 + 1;
}
}
//交换数据
public static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
(3) 归并排序
public static void mergeSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
mergeSort(arr, 0, arr.length - 1);
}
//归并具体操作
public static void mergeSort(int[] arr, int l, int r) {
if (l == r) {
return;
}
int mid = l + ((r - l) >> 1);
mergeSort(arr, l, mid);
mergeSort(arr, mid + 1, r);
merge(arr, l, mid, r);
}
//合并过程
public static void merge(int[] arr, int l, int m, int r) {
int[] help = new int[r - l + 1];
int i = 0;
int p1 = l;
int p2 = m + 1;
while (p1 <= m && p2 <= r) {
help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
}
while (p1 <= m) {
help[i++] = arr[p1++];
}
while (p2 <= r) {
help[i++] = arr[p2++];
}
for (i = 0; i < help.length; i++) {
arr[l + i] = help[i];
}
}
二、查找总结
顺序查找:不需要数列本身有序,查找性能太差,平均查找长度为(1+n)/2,时间复杂度为O(n).
二分查找: 要求数列有序
行列递增的矩阵查找:按照杨氏矩阵特殊的存储方式
分块查找:顺序查找和二分查找的改进
其他查找算法:**深度优先查找、广度优先查找、二叉树查找(先、中、后、层序遍历)**等。
(1) 二分查找
/**
* 递归实现的二分查找
* @param key
*/
public int SearchRecursion(int key)
{
if(array!=null)
{
return searchRecursion(key,0,array.length-1);
}
return -1;
}
private int searchRecursion(int key, int start, int end)
{
// TODO Auto-generated method stub
if(start>end)
{
return -1;
}
int mid=start+(end-start)/2;
if(array[mid]==key)
{
return mid;
}
else if(array[mid]三、字符串匹配KMP
经典KMP 算法
//方法:获得模式串在母串的位置
public static int KMP(String s,String m){
if(s==null||m==null||m.length()<1||s.length()0){
cn=next[cn];
}else{
next[pos++]=0;
}
}
return next;
}
四、二叉树的遍历
public static class Node {
public int value;
public Node left;
public Node right;
public Node(int data) {
this.value = data;
}
}
//先序遍历(递归)
public static void preOrderRecur(Node head) {
if (head == null) {
return;
}
System.out.print(head.value + " ");
preOrderRecur(head.left);
preOrderRecur(head.right);
}
//中序遍历(递归)
public static void inOrderRecur(Node head) {
if (head == null) {
return;
}
inOrderRecur(head.left);
System.out.print(head.value + " ");
inOrderRecur(head.right);
}
//后序遍历(递归)
public static void posOrderRecur(Node head) {
if (head == null) {
return;
}
posOrderRecur(head.left);
posOrderRecur(head.right);
System.out.print(head.value + " ");
}
//先序遍历(非递归)
public static void preOrderUnRecur(Node head) {
System.out.print("pre-order: ");
if (head != null) {
Stack stack = new Stack();
stack.add(head);
while (!stack.isEmpty()) {
head = stack.pop();
System.out.print(head.value + " ");
if (head.right != null) {
stack.push(head.right);
}
if (head.left != null) {
stack.push(head.left);
}
}
}
System.out.println();
}
//中序遍历(非递归)
public static void inOrderUnRecur(Node head) {
System.out.print("in-order: ");
if (head != null) {
Stack stack = new Stack();
while (!stack.isEmpty() || head != null) {
if (head != null) {
stack.push(head);
head = head.left;
} else {
head = stack.pop();
System.out.print(head.value + " ");
head = head.right;
}
}
}
System.out.println();
}
//后序遍历(非递归)
public static void posOrderUnRecur2(Node head) {
System.out.print("pos-order: ");
if (head != null) {
Stack s1 = new Stack();
Stack s2 = new Stack();
s1.push(head);
while (!s1.isEmpty()) {
head = s1.pop();
s2.push(head);
if (head.left != null) {
s1.push(head.left);
}
if (head.right != null) {
s1.push(head.right);
}
}
while (!s2.isEmpty()) {
System.out.print(s2.pop().value + " ");
}
}
System.out.println();
}
//后序遍历(非递归)
public static void posOrderUnRecur2(Node h) {
System.out.print("pos-order: ");
if (h != null) {
Stack stack = new Stack();
stack.push(h);
Node c = null;
while (!stack.isEmpty()) {
c = stack.peek();
if (c.left != null && h != c.left && h != c.right) {
stack.push(c.left);
} else if (c.right != null && h != c.right) {
stack.push(c.right);
} else {
System.out.print(stack.pop().value + " ");
h = c;
}
}
}
System.out.println();
}
//层序遍历
public static void levelTraverse(Node root){
if(root == null)
return;
Queue> queue = new LinkedList<>();//层序遍历时保存结点的队列
queue.offer(root);//初始化
while(!queue.isEmpty()){
BinaryNode node = queue.poll();
System.out.print(node.element + " ");//访问节点
if(node.left != null)
queue.offer(node.left);
if(node.right != null)
queue.offer(node.right);
}
}
五、图的遍历
(1)BFS
public static void bfs(Node node) {
if (node == null) {
return;
}
Queue queue = new LinkedList<>();
HashSet map = new HashSet<>();
queue.add(node);
map.add(node);
while (!queue.isEmpty()) {
Node cur = queue.poll();
System.out.println(cur.value);
for (Node next : cur.nexts) {
if (!map.contains(next)) {
map.add(next);
queue.add(next);
}
}
}
}
(2) DFS
public static void dfs(Node node) {
if (node == null) {
return;
}
Stack stack = new Stack<>();
HashSet set = new HashSet<>();
stack.add(node);
set.add(node);
System.out.println(node.value);
while (!stack.isEmpty()) {
Node cur = stack.pop();
for (Node next : cur.nexts) {
if (!set.contains(next)) {
stack.push(cur);
stack.push(next);
set.add(next);
System.out.println(next.value);
break;
}
}
}
}