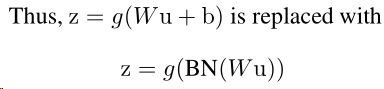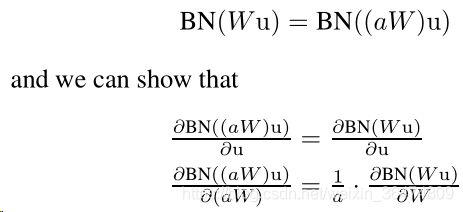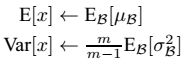批归一化Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift论文详解

背景: BN层为深度学习领域最经典结构之一，被深度网络广泛采用。我们需要深入理解BN的作用及机制。

目的: 详解BN论文。

论文地址：https://arxiv.org/abs/1502.03167v2

目录

一、概览

Motivation

Solution

Benefits

实验验证

二、问题背景

2.1 SGD中mini batch

2.2 梯度

2.3 mini-batch优点

2.4 缺点

2.5 层间运算

2.6 假定输入固定分布

梯度消失问题

之前的解决方法

BN的解决方案

2.7 Internal Covariate Shift与Batch Normalization

三、减少Internal Covariate Shift

3.1 若直接根据actiavation value更改模型

3.2 normalization的作用

三、通过mini-batch进行normalization（重要）

3.1 针对维度做简化

3.2 针对mini-batch的简化

3.3 BN算法

3.4 链式法则求导

3.5 带BN层的网络的training与Inference

3.6 带BN的卷积网络

四、BN的作用

4.1 BN保证更好的学习率

4.2 相当于对模型进行正则化

五、实验

5.1 随时间进行激活

5.2 ImageNet分类

5.2.1 加速训练

5.2.2 单网络分类

5.2.3 Ensemble Classification

六、总结与个人理解

6.1 BN解决的问题

6.2 BN与独立同分布

6.3 BN进行的条件

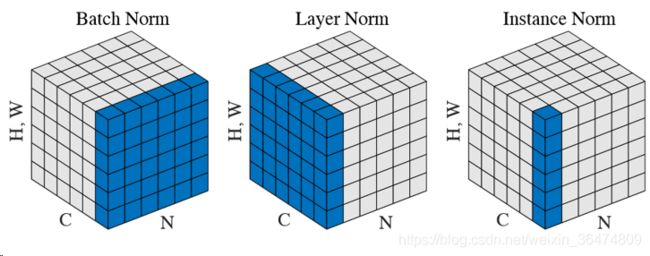
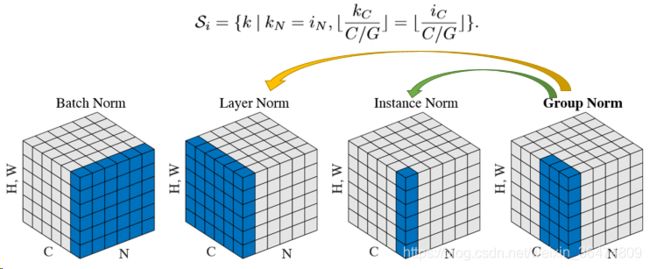
6.4 Group Normalization与Instance normalization

七、常见问题

7.1 BN可以缓解过拟合吗？

7.2 BN如何获得参数？

7.3 BN一般用在网络哪个部分？

---

一、概览

Motivation

深度网络之中每层输入的分布都不同

因此训练过程需要下面几点，从而会降低训练的速率：

• 更低的学习率
• 更好的权值初始化
• 更好的非线性

Solution

找出了问题的原因，internal covariate shift

解决的方法：将每层输入进行Normalization

将BN作为层的一部分，对每一个mini batch进行BN

Benefits

更高的学习率，不需要更好的权值初始化

作为regularizer，某些情况下减少对dropout的需要

实验验证

在当时最好的图像分类模型上采用BN，达到同样的精度需要14倍少的时间。

减少了4.9%的top-5 validation error, 减少了4.8%的test error

二、问题背景

深度学习很大程度上得益于随机梯度下降算法（SGD stcochastic gradient descent）。

2.1 SGD中mini batch

SGD通过最小化loss来优化相应的参数θ:

 x 1...N表示训练集合，l表示loss函数，θ表示网络参数。我们假定一个mini-size为m的batch。

注意：我们一般将网络需要训练的值比如卷积核称为权重（weight），然后将网络的结构或者学习率等等的信息称为参数（parameter）。但是这篇论文中的参数指代的就是wegiht，bias等等那些需要在训练过程中更新迭代的值。

2.2 梯度

2.3 mini-batch优点

• mini-batch的loss可以近似的代表整个数据集的loss
• 并且随着batch size的增大，这种estimate的质量会提升
• 单个batch的运算比分开m次的样本点的运算更加有效率
• simple and efficient

2.4 缺点

需要小心的调整网络的超参数，以及小心的初始化模型参数值

训练过程较为复杂，因为前面层的参数值对后面层有影响，所以网络深的时候，这种影响会不断积累

每层需要重新适应不同的分布

2.5 层间运算

• covariance-shift相关论文：Shimodaira, Hidetoshi. Improving predictive inference under covariate shift by weighting the log-likelihood function. Journal of Statistical Planningand Inference,90(2):227–244,October 2000.
• 处理方法，domain adapation：Jiang, Jing. A literature survey on domain adaptation of statistical classifiers, 2008

假定网络的运算如下：

 F1 and F2为网络的运算， Θ1 ,Θ2用于最小化loss。

学习Θ2可以被当成如下问题：

即用x指代相应的F1，然后代入F2，当作F2的输入。对应的梯度下降如下（m：batch size，α：学习率）：

这里，如果将x的输入分布固定，则Θ2的调整就不需要根据x的分布而做出变化。

2.6 假定输入固定分布

假定一层描述为： z = g(Wu + b)

其中，g为sigmoid激活，， u为该层输入，W为权重，b为激活。

x = Wu+b 如果x小于某个值，则梯度对于u而言则会非常小，此时网络的训练非常缓慢。

特别是网络层数较深的时候，W,b这些参数的收敛非常缓慢。

梯度消失问题

可以按照BN论文中推导的理解，

也可以按照我们自己的理解（0.9）^100=0.00002

之前的解决方法

• ReLU激活：Nair, Vinodand Hinton, GeoffreyE. Rectified linear units improve restricted boltzmann machines. In ICML, pp.807–814. Omnipress, 2010.
• 更小心的初始化：Bengio, Yoshua and Glorot, Xavier. Understanding the difficultyoftrainingdeepfeedforwardneuralnetworks.In Proceedings of AISTATS 2010, volume 9, pp. 249–256, May 2010.
• Saxe, Andrew M., McClelland, James L., and Ganguli,Surya. Exact solutions to the nonlinear dynamics of learning in deep linear neural networks. CoRR,abs/1312.6120,2013.

BN的解决方案

如果可以保证网络训练过程中，非线性的输入分布相对稳定，则可以保证optimizer不至于卡在饱和区，训练过程就可以更加快速。

2.7 Internal Covariate Shift与Batch Normalization

Batch Normalization用于减小Internal Covariate Shift.

• BN可以将输入的均值与方差固定起来，从而对梯度流的传递有更好的影响。这就更利于我们选取更大的学习率。
• BN相当于对模型进行regularizes（正则化），减少网络对dropout的需求
• BN可以避免模型进入饱和。

 关于Internal covariate Shift

对于深度学习这种包含很多隐层的网络结构，在训练过程中，因为各层参数不停在变化，所以每个隐层都会面临covariate shift的问题，也就是在训练过程中，隐层的输入分布老是变来变去，这就是所谓的“Internal Covariate Shift”，隐层的训练过程中对后续层的影响较大。

三、减少Internal Covariate Shift

训练过程中，如果固定了每层的输入x，则训练过程就可以加快。特别是被固定到0均值和单位方差的时候。

上面说法的论文证明：

• LeCun, Y., Bottou, L., Orr, G., and Muller, K. Efficient backprop. In Orr, G. and K., Muller (eds.), Neural Networks: Tricks of the trade. Springer, 1998b
• Wiesler, Simon and Ney, Hermann. A convergence analysis of log-linear training. In Shawe-Taylor, J., Zemel,R.S., Bartlett, P., Pereira, F.C.N., and Weinberger, K.Q.(eds.),Advancesin Neural Information Processing Systems 24,pp. 657–665 ,Granada, Spain, December2011

所以，我们这样认为，固定输入的统计分布，可以减少Internal Covariate Shift带来的不良影响。

3.1 若直接根据actiavation value更改模型

We could consider whitening activations at every training step or at some interval, either by modifying the network directly or by changing the parameters of the optimization algorithm to depend on the network activation values (Wiesler et al., 2014; Raiko et al., 2012;Povey et al., 2014; Desjardins & Kavukcuoglu).

缺点：

 if these modifications are interspersed with the optimization steps, then the gradient descent step may attempt to update the parameters in a way that requires the normalization to be updated, which reduces the effect of the gradient step

Thus, the combination of the update to b and subsequent change in normalization led to no change in the output of the layer nor, consequently, the loss. As the training continues, b will grow indefinitely while the loss remains fixed. This problemcan get worse if the normalizationnot only centers but also scales the activations. We have observed this empirically in initial experiments, where the model blows up when the normalization parameters are computed outside the gradient descent step

上面的方法出现的问题就是，gradient没有考虑到normalization起到的作用。

3.2 normalization的作用

我们先假定，无论对于任何输入参数，网络都可以通过normalization对输出的统计分布进行固定。

假定x为该层的输入，X为训练集的输入，normalization可以看成下面的过程：

因为等式左边的值不仅取决于该层的输入x，也取决于所有的输入样本X，并且若是x由其他层产生的话还取决于 Θ，对于BP算法，相应的Jacobians为：

将整层的输入进行normalize是非常耗费运算，并且不是连续可微。

三、通过mini-batch进行normalization（重要）

针对上述问题的缺点，作者对上述问题作了一些简化：

3.1 针对维度做简化

单独的normalize每一个每一个scalar feature（即对输入的每一个维度进行normalize）

，其中x为d维度的输入。

 the transformation inserted in the network can represent the identity transform

即gama为标准差，beta为均值，所以通过下面的这样一个映射将相应的输入的一个维度上的分布变为标准分布。并且通过相应的gama和beta还可以把之前的值给恢复出来。

3.2 针对mini-batch的简化

这里针对每个mini-batch进行估算相应的均值与方差，

假定mini-batch的值为m，batch我们描述为

如果normalize之后的值为x,则 它的线性变换为y，相应的变形为：

我们将此定义为 Batch Normalizing Transform

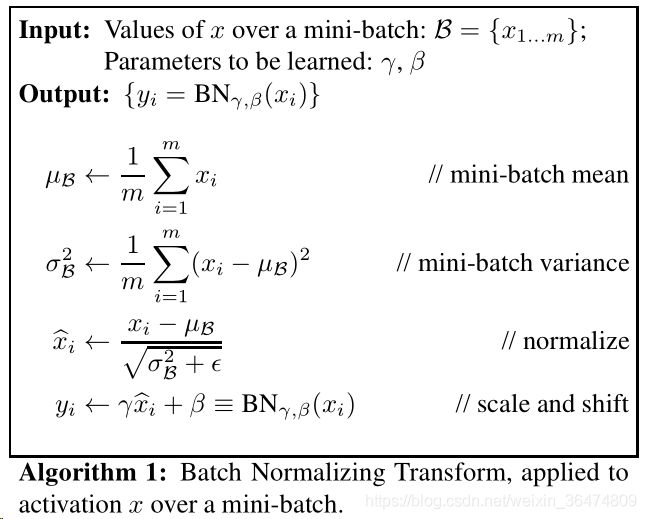
3.3 BN算法

Algorithm 1

            m = K.mean(X, axis=-1, keepdims=True)#计算均值
            std = K.std(X, axis=-1, keepdims=True)#计算标准差
            X_normed = (X - m) / (std + self.epsilon)#归一化
            out = self.gamma * X_normed + self.beta#重构变换

上面四个公式含义分别为：

• 算出mini-batch的均值
• 算出mini-batch的方差
• 将层的输入通过均值方差转变为标准分布
• 将标准分布通过均值与方差线性变换为均值beta，标准差gama的分布

注意ε为常数，用于维持mini-batch的稳定

网络的BN层的描述：

不仅取决于当前样本，也取决于 mini-batch中的其他样本。经过BN层的数值经过缩放和移位传入网络其他层。

的存在是必要的，因为

3.4 链式法则求导

3.5 带BN层的网络的training与Inference

BN的网络中，所有的网络输入层会被变为BN(x) ，网络的训练可以用Batch Normalization Descent或者Stochastic Gradient Descent来用。

mormalziation仅仅是在激活后面加一个线性变换。训练过程算法如下Algorithm 2：

3.6 带BN的卷积网络

我们将神经网络看作一个仿射变换，下面W，b为网络参数，g()为激活函数，可以为sigmoid或者ReLU。

我们假定 B为feature map所有空域上的点，假定单个feature大小为p×q 则mini-batch的尺寸为m′ = |B| = m·pq

BN针对每个feature-map学到了

algorithm 2说明了，对于同样的inference过程，BN对每个给定的feature map做了相同的线性变换。

四、BN的作用

4.1 BN保证更好的学习率

传统网络之中，高学习率可能导致梯度爆炸或者梯度消失，从而卡在局部极小值上。BN解决了这个问题。

对于BP算法，大的weight，我们用a来缩放它，相应的梯度：

因此，大weight会导致小梯度，从而不利于网络训练，我们归一化就能有更好的影响。

4.2 相当于对模型进行正则化

五、实验

5.1 随时间进行激活

LeNet上用MNIST进行实验，（a）发现随着训练的过程进行，带BN的训练更加顺畅（bc）发现，并且BN显著改善了internal covariate shift

5.2 ImageNet分类

5.2.1 加速训练

BN优点，作者探讨，具体参看原论文。

• Increase learning rate，增大学习率
• 去除dropout
• 减少L2权重正则化
• 加速学习率退化
• 减少Local Response Normalization
• 对训练样本进行更彻底的Shuffle
• 减少photometric distortions

5.2.2 单网络分类

LSVRC2012训练集

几种对比如下：

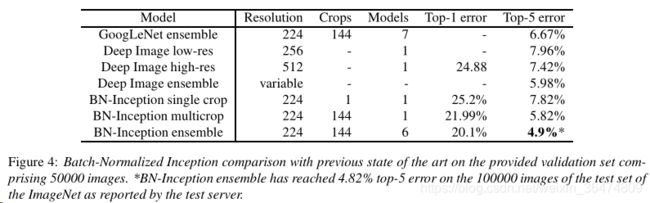
5.2.3 Ensemble Classification

六、总结与个人理解

6.1 BN解决的问题

随着层数加深的梯度消失和梯度爆炸问题，使每层独立同分布，更好的传递梯度。能够加快网络收敛。

6.2 BN与独立同分布

机器学习领域有个很重要的假设：IID独立同分布假设，就是假设训练数据和测试数据是满足相同分布的，这是通过训练数据获得的模型能够在测试集获得好的效果的一个基本保障。那BatchNorm的作用是什么呢？BatchNorm就是在深度神经网络训练过程中使得每一层神经网络的输入保持相同分布的。

6.3 BN进行的条件

BN以mini-batch为单位，针对feature的每一个维度，分开的进行normalization，所以叫做batch normalization

其实相当于batch-每维度-normalization

6.4 Group Normalization与Instance normalization

最新出的Gropu Normalization对BN进行了改进，后续可以看下group normalization相关的论文。这两种模型采用了不同的normalization的方式。

七、常见问题

7.1 BN可以缓解过拟合吗？

可以。为什么？可以看作一种数据增强的方法。具体详细的解释可以参见原论文，How Does Batch Normalization Help Optimization?

https://arxiv.org/pdf/1805.11604.pdf

粗略讲，就是，BN输入的样本特征不仅取决于自身的样本，也取决于与之同一个batch的特征。经过了BN处理后，可以看作一个样本特征在高维空间上的拉扯，可以看作一种数据增强的过程。

这种数据增强会贯穿神经网络始终，因此BN是可以缓解过拟合。

7.2 BN如何获得参数？

BN有两个参数，针对每个feature，有一个均值，和一个标准差。

BN的相应参数，是在训练过程中固定的。一旦开始测试阶段，其参数就固定下来了。

这个参数：

• 均值为均值的期望（均值的均值）
• 方差为方差的无偏估计（为什么分母要m-1，这个是概率论之中的内容 https://blog.csdn.net/qq_16587307/article/details/81328773  粗略的理解为，均值也是一个有偏的量，其中算出的均值也是有方差在里面的，所以方差m-1就要大一些）。

所以测试阶段使用的公式为：

7.3 BN一般用在网络哪个部分？

激活层前还是激活层后呢？先BN，后激活。

因为我们的目的，就是为了通过BN让网络的传递更顺畅。而加入BN之后，feature更加容易被映射到激活函数的线性区，因此梯度可以更好的传递。因此，先BN，后激活。

z=g(Wu+b)是常规的激活函数，g是激活函数，z是输出。

z=g(BN(Wu+b))偏置会被归一化处理，所以加不加b经过BN之后是一样的映射，简化为下面这样：

z=g(BN(Wu))