LeedCode算法题——盛最多水的容器

题目

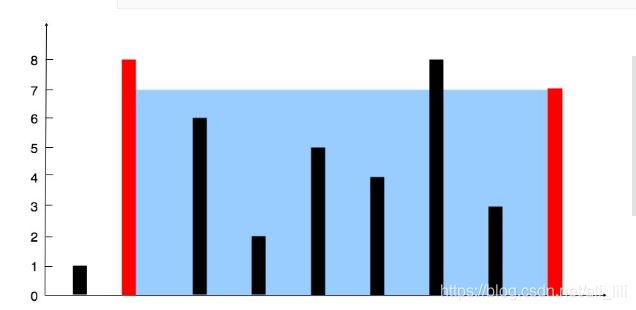
给定 n 个非负整数 a1，a2，…，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器，且 n 的值至少为 2。

图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例:

输入: [1,8,6,2,5,4,8,3,7]
输出: 49

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/container-with-most-water

解题

一开始我拿到这个题，觉得不难啊，于是就是暴力法：

class Solution {
    public int maxArea(int[] height) {
        int result=0;
        for(int i=0;iresult)
                    result=temp;
            }
        return result;
    }
}

这个解是解出来了，但是明显不符合题目是中等难度的意愿，并且那个运行时间真的是：

于是就在论坛看各位大佬的解法，真的是眼前一亮：

	public int maxArea(int[] a) {
		 int max = 0;
		 for(int i = 0, j = a.length - 1; i < j ; ){
			 int minHeight = a[i] < a[j] ? a[i ++] : a[j --];
			 max = Math.max(max, (j - i + 1) * minHeight);
		 }
		 return max;
	 }

这个代码真的是太美了：

运行了一下，这个结果真的是，佩服佩服。主要是通过双指针，一个从前往后，一个从后往前，哪个小的就下一个。但是我就很好奇了，这样子中间会不会忽略了最优解了？自己是想不出来了，看到了一位大佬的证明：

这个真的证明的很漂亮，从理论上证明了这个做法的成立。但是我又很好奇，被忽略的那些容器有多少呢，都是些什么样的容器了？于是自己画了一个二叉树：

其实最后算的也就红圈里面的那么多，其他的都是省略的，然后自己手动算几个，发现真的不会漏了最优解。树的每一层所对应的容器的底其实是一样的，已第二层的（0,7）和（1,8）为例，容器底都是7，但是高就不一样了，（0,7）的高分别是1和3，取最小值，也就是容器的高是1，明显不符合。而且如果（0,7）是比（1,8）要优的解的话，那么从（0,8）就不会是去到（1,8），而是去到（0,7）了。
刚开始我会很疑惑，第三层的底长为6，而其中（2,8）容器的盛水量明明比（1,7）的大，但是按照算法，是从（1,8）去到了（1,7），这是为什么了？其实是因为（2,8）的盛水量虽然比（1,7）大，但是却没有比（1,8）大。从（1,8）往下，其实是容器的底部在缩小，而只有容器的长变大，才有可能是最优解，所以程序是舍弃掉了较短的一边，继续往下。