MATLAB与线性代数
MATLAB与线性代数
- 数组的表示,冒号的用法
- 线性间隔向量
- 对数化间隔向量
- 显示格式的设置
- 矩阵的加法和减法
- 数组的乘法与除法;矩阵积和除法
- 方阵的行列式
- 矩阵的转置
- 常见矩阵
数组的表示,冒号的用法
一、语法知识
1.j:k 相当于向量[j,j+1,j+2,k]
2.j:i:k [j,j+i,j+2i,…k]
3.A(:,j) 矩阵A的j列
4.A(i,:) 矩阵A的i行
二、例题
例题1 建立从1-100,步长为3的数组
>> x=1:3:100
>> A(1,:)=1:5;
>> A(2,:)=6:10;
>> A(3,:)=11:15
A =
1 2 3 4 5
6 7 8 9 10
11 12 13 14 15
例题3计算数组1,2, 。。。。 100之和
>> x=1:100;
>> sum(x)
ans =
5050
线性间隔向量
一、语法知识
产生一个行向量,从x1到x2之间,均匀分布n个数,书写格式linspace(x1,x2,n)
二、例题
例题1.用linspace列出1-5之间的20个等距数组
>> linspace(1,5,20)
ans =
1 至 12 列
1.0000 1.2105 1.4211 1.6316 1.8421 2.0526 2.2632 2.4737 2.6842 2.8947 3.1053 3.3158
13 至 20 列
3.5263 3.7368 3.9474 4.1579 4.3684 4.5789 4.7895 5.0000
对数化间隔向量
一、语法知识
产生一个行向量,从10x1到10x2之间,均匀分布n个数,书写格式logspace(x1,x2,n)
二、例题
例题1.用logspace列出10-100之间的以对数刻度分布的12个数
>> logspace(1,2,12)
ans =
10.0000 12.3285 15.1991 18.7382 23.1013 28.4804 35.1119 43.2876 53.3670 65.7933 81.1131 100.0000
显示格式的设置
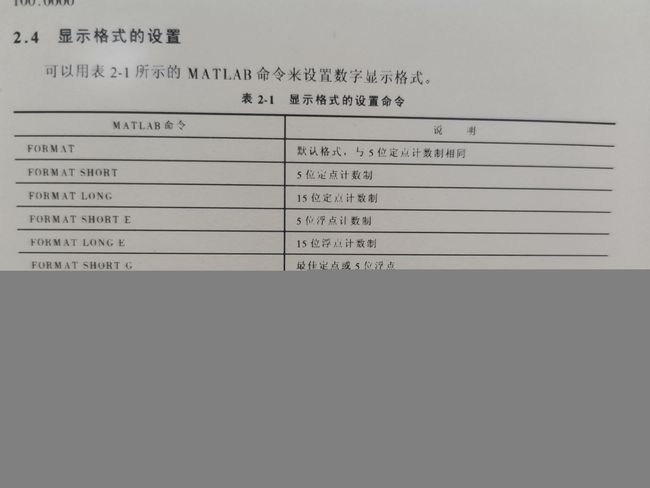
用format short,format long,format rat 分别显示Π的值
>> format short
>> pi
ans =
3.1416
>> format long
>> pi
ans =
3.141592653589793
>> format rat
>> pi
ans =
355/113
矩阵的加法和减法
例题1
>> A=[1 2 3;4 5 6;7 8 10]
A =
1 2 3
4 5 6
7 8 10
>> B=[1 3 5 ;7 9 11; 13 15 16]
B =
1 3 5
7 9 11
13 15 16
>> B-A
ans =
0 1 2
3 4 5
6 7 6
>> A+B
ans =
2 5 8
11 14 17
20 23 26
>> A(1,:)=1:3;
>> A(2,:)=4:6;
>> A(3,:)=7:9
A =
1 2 3
4 5 6
7 8 9
>> C(1,:)=1:2:5;
>> C(2,:)=7:2:11;
>> C(3,:)=[13 15 16]
C =
1 3 5
7 9 11
13 15 16
>> A+C
ans =
2 5 8
11 14 17
20 23 25
>> A-C
ans =
0 -1 -2
-3 -4 -5
-6 -7 -7
>>
数组的乘法与除法;矩阵积和除法
>> A=[1 2 3;2 4 6;3 6 12]
A =
1 2 3
2 4 6
3 6 12
>> B=[1 2 3]
B =
1 2 3
>> B=[B;B;B] %定义矩阵的方法
B =
1 2 3
1 2 3
1 2 3
>> A.*B %对应元素的乘积
ans =
1 4 9
2 8 18
3 12 36
>> A*B %矩阵的乘积
ans =
6 12 18
12 24 36
21 42 63
>> A./B %对应元素的除法
ans =
1 1 1
2 2 2
3 3 4
>> A/B %矩阵的右除 ans*B=A
警告: 矩阵为奇异工作精度。
ans =
0/0 0/0 0/0
0/0 0/0 0/0
0/0 0/0 0/0
>> A\B %矩阵B被A左除,得到的ans*A=B
警告: 矩阵为奇异工作精度。
ans =
1/0 1/0 1/0
-1/0 -1/0 -1/0
-2/3 -4/3 -2
>>
方阵的行列式
求矩阵行列式的值:det(A)。
注意A为方阵,才有行列式;行列式是一个标量值
>> A=[1 2 3;4 5 6;7 8 10]
A =
1 2 3
4 5 6
7 8 10
>> det(A)
ans =
-3
矩阵的转置
B=A’
B是A的转置矩阵,行列元素呼唤A[i][j]=A[j][i]
>> A=[1 2 3;4 5 6;7 8 10]
A =
1 2 3
4 5 6
7 8 10
>> B=A'
B =
1 4 7
2 5 8
3 6 10
常见矩阵
1.单位矩阵:对角线全为1,其他元素全为0
eye(m,n);eye(m)
>> eye(4)
ans =
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
>> eye(3,4)
ans =
1 0 0 0
0 1 0 0
0 0 1 0
>>
2.全1矩阵:所有元素都是1
ones(m,n);ones(m)
>> ones(4)
ans =
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1
>> ones(2,3)
ans =
1 1 1
1 1 1
3.零矩阵:元素全为0 zeros(m,n)m行n列
zeros(m)
>> zeros(4)
ans =
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
>> zeros(2,3)
ans =
0 0 0
0 0 0
4.魔方矩阵:magic(n)n阶;magic(m,n)
>> magic(4)
ans =
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
>> magic(3,4)
错误使用 magic
输入参数太多。
5.Pascal矩阵 :pascal(m,n)n只能取0,1,2
>> pascal(4)
ans =
1 1 1 1
1 2 3 4
1 3 6 10
1 4 10 20
>> pascal(4,1)
ans =
1 0 0 0
1 -1 0 0
1 -2 1 0
1 -3 3 -1
6.Hilbert矩阵:Hilb(m,n)
元素的值由行数和列数决定的
为(1/(i+j-1))
>> hilb(4)
ans =
1.0000 0.5000 0.3333 0.2500
0.5000 0.3333 0.2500 0.2000
0.3333 0.2500 0.2000 0.1667
0.2500 0.2000 0.1667 0.1429
>> format rat
>> ans
ans =
1 1/2 1/3 1/4
1/2 1/3 1/4 1/5
1/3 1/4 1/5 1/6
1/4 1/5 1/6 1/7
>>
7.均匀分布的随机矩阵
rand(m,n) 随机数是选择(0,1)区间的
>> A1=rand(4) %均匀分布
A1 =
0.8147 0.6324 0.9575 0.9572
0.9058 0.0975 0.9649 0.4854
0.1270 0.2785 0.1576 0.8003
0.9134 0.5469 0.9706 0.1419
8.正态分布的随机矩阵
randn(m,n)
>> A2=randn(4)
A2 =
-0.1241 0.6715 0.4889 0.2939
1.4897 -1.2075 1.0347 -0.7873
1.4090 0.7172 0.7269 0.8884
1.4172 1.6302 -0.3034 -1.1471
