数据结构：哈夫曼树的建立与哈夫曼编码的实现

哈夫曼树

哈夫曼树，也称最优二叉树，是数据结构的一个重要内容，实际运用中我们通过哈夫曼编码来大幅度提高无损压缩的比例。

弄清哈夫曼树，我们首先要弄清以下四个概念。

概念1：什么是路径？

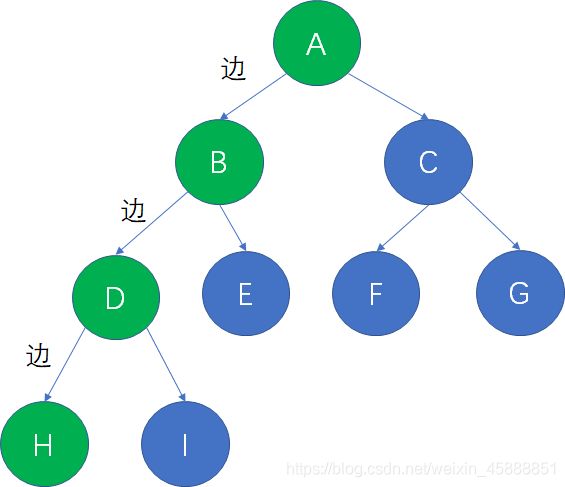
在一棵树中，从一个结点到另一个结点所经过的所有结点，被我们称为两个结点之间的路径。

上面的二叉树当中，从根结点A到叶子结点H的路径，就是A，B，D，H。

概念2：什么是路径长度？

在一棵树中，从一个结点到另一个结点所经过的“边”的数量，被我们称为两个结点之间的路径长度。

仍然用刚才的二叉树举例子，从根结点A到叶子结点H，共经过了3条边，因此路径长度是3。

概念3：什么是结点的带权路径长度？

树的每一个结点，都可以拥有自己的“权重”（Weight），权重在不同的算法当中可以起到不同的作用。

结点的带权路径长度，是指树的根结点到该结点的路径长度，和该结点权重的乘积。

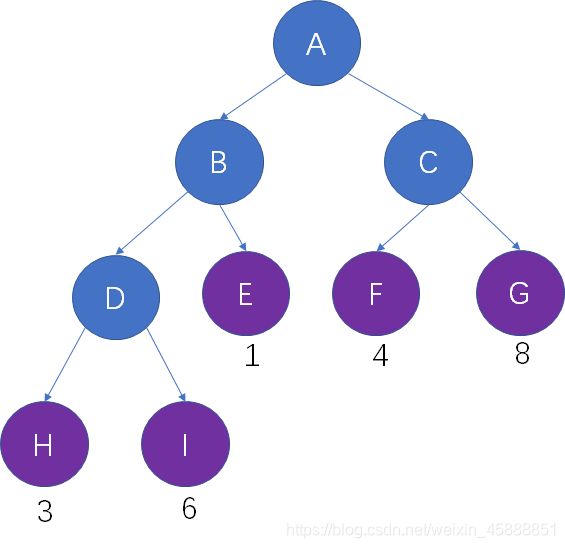
假设结点H的权重是3，从根结点到结点H的路径长度也是3，因此结点H的带权路径长度是 3 X 3 = 9。

概念4：什么是树的带权路径长度？

在一棵树中，所有叶子结点的带权路径长度之和，被称为树的带权路径长度，也被简称为WPL。

仍然以这颗二叉树为例，树的路径长度是 3X3 + 6X3 + 1X2 + 4X2 + 8X2 = 53。

接下来，我们便可以引出哈夫曼树的概念了：
给定N个权值作为N个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。

举个例子，给定权重分别为1，3，4，6，8的叶子结点，我们应当构建怎样的二叉树，才能保证其带权路径长度最小？

原则上，我们应该让权重小的叶子结点远离树根，权重大的叶子结点靠近树根。

下图左侧的这棵树就是一颗哈夫曼树，它的WPL是46，小于之前例子当中的53：

需要注意的是，同样叶子结点所构成的哈夫曼树可能不止一颗，下面这几棵树都是哈夫曼树：

假设有6个叶子结点，权重依次是2，3，7，9，18，25，如何构建一颗哈夫曼树，也就是带权路径长度最小的树呢？

第一步：构建森林

我们把每一个叶子结点，都当做树一颗独立的树（只有根结点的树），这样就形成了一个森林：

在上图当中，右侧是叶子结点的森林，左侧是一个辅助队列，按照权值从小到大存储了所有叶子结点。至于辅助队列的作用，我们后续将会看到。

第二步：选择当前权值最小的两个结点，生成新的父结点。

借助辅助队列，我们可以找到权值最小的结点2和3，并根据这两个结点生成一个新的父结点，父节点的权值是这两个结点权值之和：

第三步：从队列中移除上一步选择的两个最小结点，把新的父节点加入队列。

也就是从队列中删除2和3，插入5，并且仍然保持队列的升序：

第四步：选择当前权值最小的两个结点，生成新的父结点。

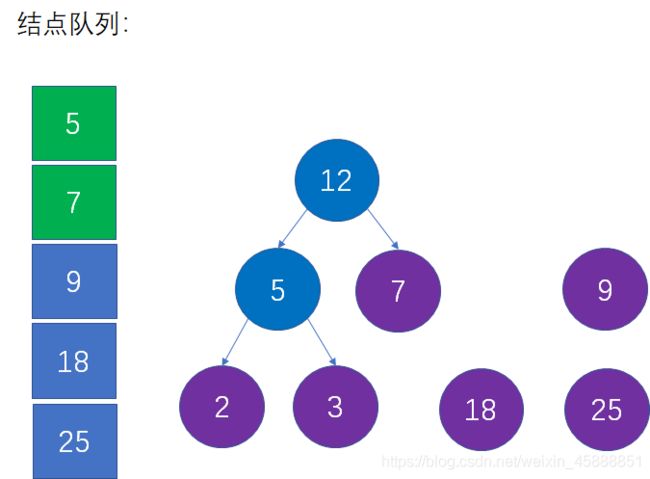
这是对第二步的重复操作。当前队列中权值最小的结点是5和7，生成新的父结点权值是5+7=12：

第五步：从队列中移除上一步选择的两个最小结点，把新的父节点加入队列。

这是对第三步的重复操作，也就是从队列中删除5和7，插入12，并且仍然保持队列的升序：

第六步：选择当前权值最小的两个结点，生成新的父结点。

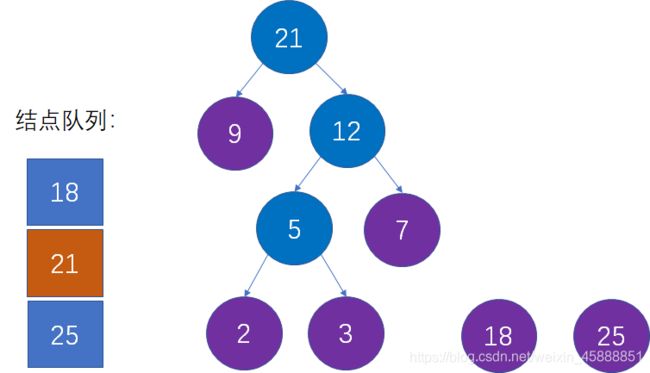
这是对第二步的重复操作。当前队列中权值最小的结点是9和12，生成新的父结点权值是9+12=21：

第七步：从队列中移除上一步选择的两个最小结点，把新的父节点加入队列。

这是对第三步的重复操作，也就是从队列中删除9和12，插入21，并且仍然保持队列的升序：

第八步：选择当前权值最小的两个结点，生成新的父结点。

这是对第二步的重复操作。当前队列中权值最小的结点是18和21，生成新的父结点权值是18+21=39：

第九步：从队列中移除上一步选择的两个最小结点，把新的父节点加入队列。

这是对第三步的重复操作，也就是从队列中删除18和21，插入39，并且仍然保持队列的升序：

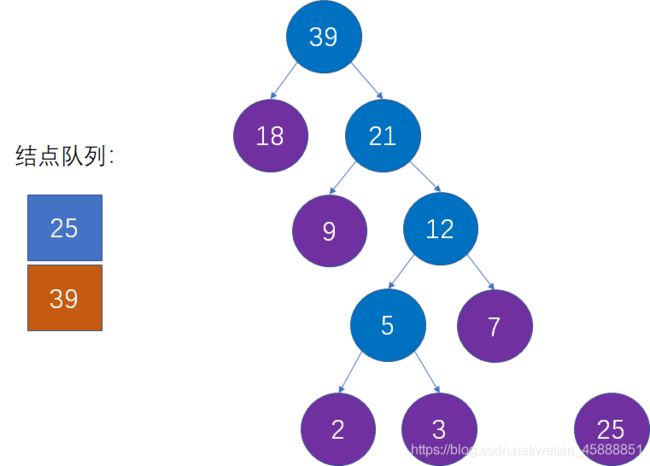
第十步：选择当前权值最小的两个结点，生成新的父结点。

这是对第二步的重复操作。当前队列中权值最小的结点是25和39，生成新的父结点权值是25+39=64：

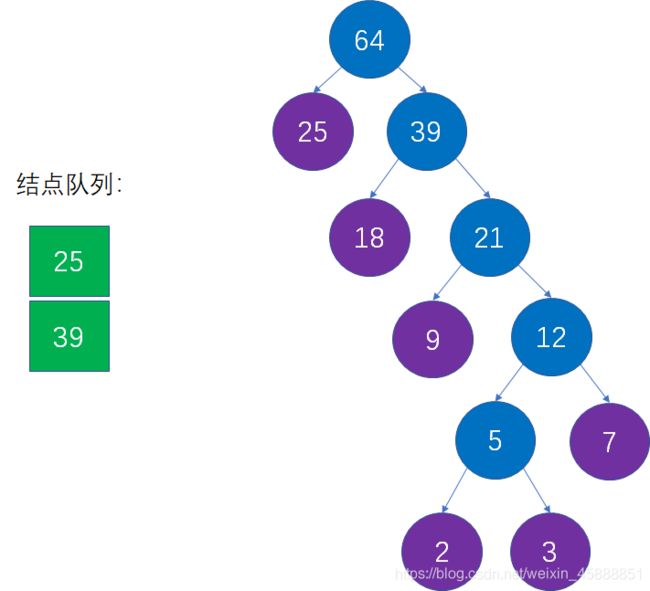
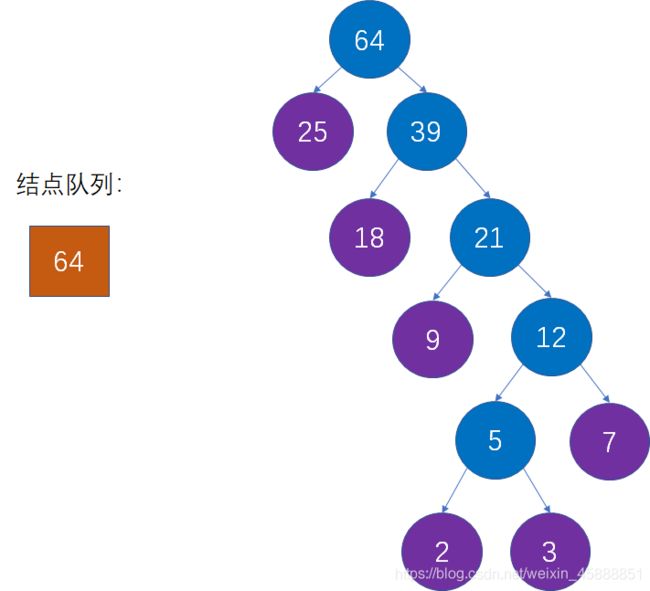
第十一步：从队列中移除上一步选择的两个最小结点，把新的父节点加入队列

这是对第三步的重复操作，也就是从队列中删除25和39，插入64：

此时，队列中仅有一个结点，说明整个森林已经合并成了一颗树，而这棵树就是我们想要的哈夫曼树：

哈夫曼编码

那么，建立哈夫曼树，在我们实际的数据结构中又有什么运用呢？这便要轮到哈夫曼编码出场了。

首先，我们要知道，计算机信息的存储是通过各种各样的编码实现的，比如二进制编码，ASCII编码等。

在在ASCII码当中，把每一个字符表示成特定的8位二进制数来存储，显然，这是一种等长编码。

这种编码设计简单，方便读写，但同时，因为计算机的存储空间以及网络带宽是有限的，等长编码的结果太长，会占用较大的资源。

所以哈夫曼编码就是针对此设计的一种不等长编码，其具有两个重要特征：

1.任何一个字符编码，都不是其他字符编码的前缀。
2.信息编码的总长度最小。

哈夫曼编码的编码规则

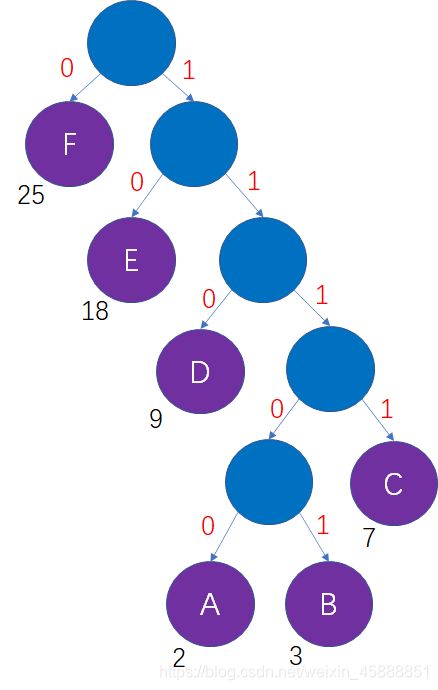
哈夫曼树的每一个结点包括左、右两个分支，二进制的每一位有0、1两种状态，我们可以把这两者对应起来，结点的左分支当做0，结点的右分支当做1。

这样一来，从哈夫曼树的根结点到每一个叶子结点的路径，都可以等价为一段二进制编码：

上述过程借助哈夫曼树所生成的二进制编码，就是哈夫曼编码。

编码前缀问题带来的歧义

显然，这个问题是不存在的，因为每一个字符对应的都是哈夫曼树的叶子结点，从根结点到这些叶子结点的路径并没有包含关系，最终得到的二进制编码自然也不会是彼此的前缀。

代码实现

package 哈夫曼树;

import java.util.PriorityQueue;
import java.util.Queue;


public class HFMtree{

	private HTreeNode root;
	private HTreeNode[] nodes;
	
	//定义一个哈树节点
	public class HTreeNode implements Comparable<HTreeNode>{
		
		String s;//代表的字符 只有叶节点才会有的
		int weight;
		private HTreeNode left;
		private HTreeNode right;
	
		
		public HTreeNode(int weight){
			this.weight = weight;
		}
		
		public HTreeNode(int weight, HTreeNode left, HTreeNode right){
			this.weight = weight;
			this.left = left;
			this.right = right;
		}
		
		//Java的优先队列是小根堆(堆顶的元素为最小元素)，是根据自然排序来进行优先级的判断，
		//所以自定义的类想要加进优先队列中必须先实现Comparable接口，编写compareTo的方法，方可以使用
		public int compareTo(HTreeNode o){
			//若指定的结点权重大于参数（o）结点的权重，则返回1（true）
			return new Integer(this.weight).compareTo(new Integer(o.weight));
		}
		
		
	}

	
	//根据权值，建一个哈夫曼树
	public void createHFMTree(int[] weights){ 
		
		//优先队列，用于辅助构建哈夫曼树
		Queue<HTreeNode> nodeQueue = new PriorityQueue<HTreeNode>();
		nodes = new HTreeNode[weights.length];
		
		//构建森林，初始化nodes数组
		for(int i=0; i<weights.length; i++){
			nodes[i] = new HTreeNode(weights[i]);
			nodeQueue.add(nodes[i]);
			
		}
		//循环后的队列各结点权重由小到大排列
		
		//主循环，当结点队列只剩一个结点时结束，建立哈夫曼树
		while(nodeQueue.size() > 1){
			
			//返回第一个元素，并在队列中删除，队列长度不断缩小
			HTreeNode left = nodeQueue.poll();
			HTreeNode right = nodeQueue.poll();
			
			//创建新结点作为两结点的父节点
			HTreeNode parent = new HTreeNode(left.weight + right.weight, left, right);
			nodeQueue.add(parent);
			
		}
		
		//获得所建树的根结点
		//返回第一个元素（即根结点），并在队列中删除
		root = nodeQueue.poll();
	
	}
	
	//按照前序遍历输出
	public void output(HTreeNode head){
		if(head != null){
			System.out.println(head.weight);
			output(head.left);
			output(head.right);
		}
	}
	
	//用递归的方式，填充各个结点的二进制编码
	public void encode(HTreeNode node, String s){
		if(node != null){
			node.s = s;
			encode(node.left, node.s+"0");
			encode(node.right, node.s+"1");
		}
	}
	
	//输出哈树上每个叶节点的01编码，左0右1
	public void printTreeCode(String[] sa, int[] weights){
		for(int i=0; i<weights.length; i++){
			System.out.println(sa[i] +":" + nodes[i].s);
		}
	} 
	
	public static void main(String[] args) {
		
		int[] weights = new int[]{7, 8, 2, 1, 1};
		String[] sa = new String[]{"a","b","c","d","e",};
		
		HFMtree huffmanTree = new HFMtree();
	    huffmanTree.createHFMTree(weights);
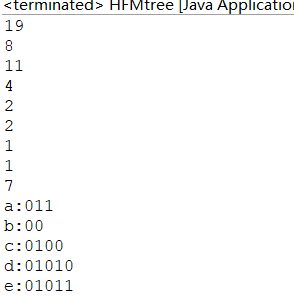
	    huffmanTree.output(huffmanTree.root);
	    huffmanTree.encode(huffmanTree.root, "0");
	    huffmanTree.printTreeCode(sa, weights);
	}
}

代码运行后的输出结果：