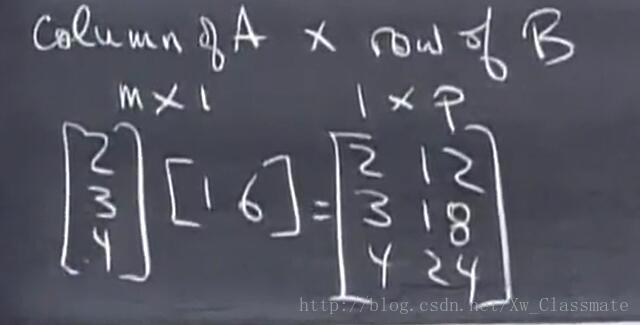线性代数：矩阵乘法和逆矩阵

本节是网易公开课上的麻省理工大学线性代数课程第三节： 矩阵乘法和逆矩阵 的学习笔记。

矩阵乘法

矩阵相乘，并不一定要求是方阵。

如果矩阵 A 是一个 mxn 的矩阵（m行，n列），则矩阵 B 必须是一个 nxp（n行，p列）的矩阵，这样两者才能相乘，相乘的结果矩阵 C 是一个 mxp（m行，p列）的矩阵。

一般法则

假设 AB=C 。那 C34=?

答案：

C34=A3,:⋅B:,4=A3,1B1,4+A3,2⋅B2,4=∑A3,kBk,4

其中： A3,:⋅B:,4 表示矩阵 A 的第三行元素（一个向量）和矩阵 B 的第四列元素（一个向量）的点积。

列方法

继续上面的 AB=C 。

矩阵 A(mxn) 乘以矩阵 B(nxp) 可以理解为矩阵 A 分别乘以矩阵 B 的每一列的向量（总共p个），得到的结果分别对应矩阵 C 中对应的某列元素。而矩阵 A 乘以向量可以理解为矩阵 A 中各列的线性组合（可参看 第一节 中的知识）。

这样，矩阵 C 中的每一列其实就是矩阵 A 中的每一列的线性组合，而矩阵 B 中的数字相当于告诉怎么进行线性组合。

行方法

矩阵 A(mxn) 乘以矩阵 B(nxp) 可以理解为矩阵 A 中的每一行的向量乘以矩阵 B，得到的结果分别对应矩阵 C 中对应的某行元素。而向量乘以矩阵 B 可以理解为矩阵 B 中各行的线性组合。

这样，矩阵 C 中的每一行其实就是矩阵 B 中的每一行的线性组合，而矩阵 A 中的数字相当于告诉怎么进行线性组合。

列乘以行

如果使用一个行向量(1xn)乘以一个列向量(nx1)结果是一个数，那使用列向量(mx1)乘以行向量(1xp)呢？

结果会是一个mxn矩阵，这个矩阵非常特殊。它的每一列元素分别是列向量的线性组合，它的每一行元素都分别是行向量的线性组合。

也就是说，结果矩阵的每一行都依赖于向量 [1,6] ，如果画出这个矩阵的所有行向量，它们都是同一个方向。同理，如果画出这个矩阵的所有列向量，它们也都是同一个方向的。

换一种说法，该矩阵的行空间是一条直线，其所有的行向量都在过(1,6) 这两点的直线上。

基于这种思路，我们来使用列乘以行来解决矩阵相乘的问题。AB 等于矩阵 A 各列与矩阵 B 各行乘积之和。

分块乘法

可以将矩阵 A 分成几部分，简单起见，分成4部分，即四块。简单起见，假设矩阵 A 是方阵（mxm），矩阵 B 也是方阵（mxm）。一张图说明问题：

逆矩阵

可逆（非奇异）

假设一个矩阵 A ，如果存在左逆，则： A−1A=I ，如果存在右逆，则： AA−1=I ，其中 A−1 表示 A 的逆矩阵， I 表示单位矩阵。如果 A 是方阵的话，左逆矩阵等于右逆矩阵。

如果矩阵存在可逆矩阵，则称该矩阵是可逆的、或者非奇异的。

不可逆（奇异）

假设矩阵 A 为：

[1236]

该矩阵不可逆，考虑下为什么呢？

解释方式一：

矩阵可逆的前提是该矩阵乘以一个矩阵能够得到单位矩阵或者一个矩阵乘以该矩阵能够得到单位矩阵。结合上面将的矩阵乘法知识，如果 A 乘以一个矩阵，那么这个结果矩阵的每一列是 A 的每一列的线性组合，考虑下，因为 A 中的两列向量共线，经过点（1,2），而单位矩阵的列向量[1,0] 和 [0,1] 不在其上，所以是这种情况下是不可能得到单位矩阵的。

解释方式二：

如果存在非零向量 X ，使得 AX=0 ,那么矩阵不可逆。

[1236][−31]=[00]

也就是说，如果矩阵中的一列对线性组合毫无贡献，矩阵不可能有逆。

我们可以假设如果存在一个非零向量 X，使得 AX=0 ，且我们也假设 A 存在可逆矩阵 A−1 。则：

A−1AX=A−10

化简后得： X=0。这明显不正确，所以假设不成立。

解释方式三：

如果矩阵的行列式为0，则该矩阵不可逆。

高斯-若尔当消元法

假设矩阵 A 如下：

[1237]

可以证明，该矩阵是可逆的，假设存在一个矩阵，使得：

[1237][abcd]=[1001]

通过上面的关系，我们可以根据矩阵乘法中的列方法得到一个方程组（以矩阵形式表示出来）：

[1237][ab]=[10][1237][cd]=[01]

现在，我们来构造一个新的矩阵，该矩阵包含两部分，一部分是原始矩阵 A ，另一部分是单位矩阵 I。

[1237||1001]

对该矩阵的左边进行消元，将其变为单位矩阵，此时右边部分就为矩阵 A 的逆矩阵。

[1237||1001]→row2=row2−2row1[1031||1−201]→row1=row1−3row2[1001||7−2−31]

验证结果：

[1237][7−2−31]=[1001]