MATLAB与线性代数2
MATLAB和线性代数
- 矩阵的大小
- 矩阵的秩
- 向量的范数
- 矩阵的范数
- 矩阵的条件数
矩阵的大小
size(A)=(m,n,s……)
size(A,1)=m
用于构造和已知矩阵大小相同的矩阵
>> B(:,:,1)=magic(3)
B =
8 1 6
3 5 7
4 9 2
>> B(:,:,2)=pascal(3)
B(:,:,1) =
8 1 6
3 5 7
4 9 2
B(:,:,2) =
1 1 1
1 2 3
1 3 6
>> B(:,:,3)=zeros(3)
B(:,:,1) =
8 1 6
3 5 7
4 9 2
B(:,:,2) =
1 1 1
1 2 3
1 3 6
B(:,:,3) =
0 0 0
0 0 0
0 0 0
>> B(:,:,4)=ones(3)
B(:,:,1) =
8 1 6
3 5 7
4 9 2
B(:,:,2) =
1 1 1
1 2 3
1 3 6
B(:,:,3) =
0 0 0
0 0 0
0 0 0
B(:,:,4) =
1 1 1
1 1 1
1 1 1
>> size(B)
ans =
3 3 4
>> size(B,1)
ans =
3
>> size(B,2)
ans =
3
>> size(B,3)
ans =
4
>> C=ones(size(pascal(4)))
C =
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1
>> C=eye(size(pascal(4)))
C =
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
矩阵的秩
矩阵的秩是对矩阵行(或列)线性不相关数的评估,满秩的话则是独立的,即是线性无关
rank(A)
B =
8 1 6
3 5 7
4 9 2
>> rank(B)
ans =
3
向量的范数
范数是长度
>> v=[1 2 3 4]
v =
1 2 3 4
>> norm(v,1)
ans =
10
>> norm(v,2)
ans =
2525/461
>> format long
>> ans
ans =
5.477225575051661
>> format short
>> ans
ans =
5.4772
>> norm(v,+inf)
ans =
4
>> norm(v,-inf)
ans =
1
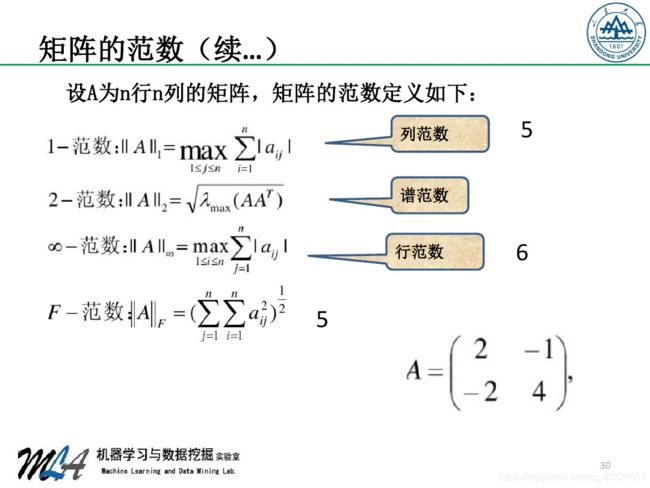
矩阵的范数
>> B1=[1 2 3 4;2 3 5 8;1 3 5 7;3 4 7 11]
B1 =
1 2 3 4
2 3 5 8
1 3 5 7
3 4 7 11
>> norm(B1,1) %列和最大值
ans =
30
>> max(sum(B1))
ans =
30
>> norm(B1,2)
ans =
20.2435
>> max(svd(B1))
ans =
20.2435
>> norm(B1,inf) %行和最大值
ans =
25
>> max(sum(B1'))
ans =
25
>> norm(B1,'fro')
ans =
20.2731
>> sum(abs(B1(1:16)).^2).^(1/2)
ans =
20.2731
>> sqrt(sum(diag(B1'*B1)))
ans =
20.2731
S = sum(X) is the sum of the elements of the vector X. If X is a matrix, S is a row(行) vector with the sum over each column.
矩阵的条件数
1.矩阵的条件数是一个用来测量线性方程组的解对数据输入误差的灵敏度