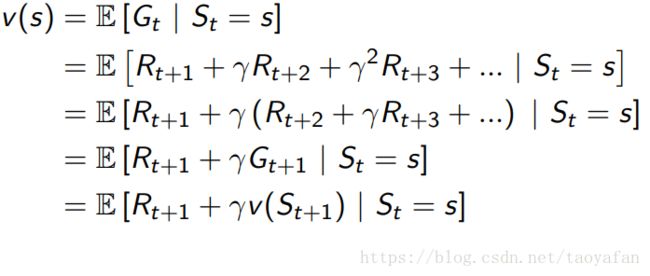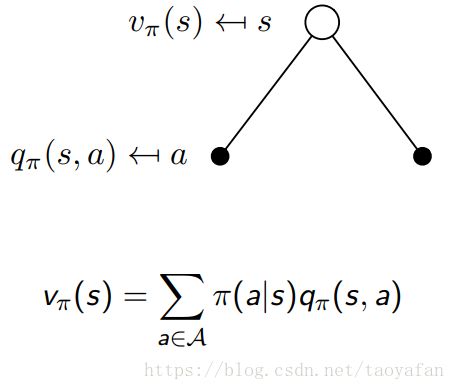David silver 强化学习公开课笔记（二）：MP、MRP、MDP
1 引言
1.1 Markov 的性质
正如上一节课提到的，Markov 状态表示当前的状态包括了历史所有的信息，也就是给定当前状态，未来和历史是独立的。通俗的说就是未来只和现在有关，和过去是没有关系的！其实也不能说和过去是没有关系，而是现在状态包括了所有的历史。有点绕。。还是看下面的定义式：
所有的 RL 的问题都能表示为一个 MDP。关于什么是 MDP，下面再说。
1.2 状态转移矩阵
从状态 s 转移到状态 s' 的定义式为：
状态转移矩阵为：
其中每一行的和为1。
1.3 马尔科夫过程（马尔科夫链）
一系列状态所组成的序列，是一个元祖
2 Markov Reward Process
2.1 MRP
在马尔科夫链的基础上增加了奖赏 reward 和折扣因子 
。其中 reward 为进入某个状态后得到的奖赏，折扣因子的作用是表示未来的 reward 对当前的动作所带来的收益，折扣因子越大则未来的 reward 对当前的动作影响越大，具体公式在2.2将会介绍。先看 PPT 中的定义式：
2.2 Return
Return 
表示一个马尔科夫过程中 t 时刻的状态所能得到的总奖赏。注意是针对一个特定的 MP 而言的，这里还不考虑动作，不同的 MP 算出来的 不一样。
2.3 Value Function（值函数）
其实就是 ，表示一个状态的好坏的一个值，值越大说明这个状态越好，也就意味着以后有更大的概率可以获得更多的 reward。
注意：这里的值函数表示的是状态值函数，及表示一个状态的好坏，而非动作的好坏。
2.4 贝尔曼方程
一看公式就知道了，其实就是原有的 要一直向后加，但是实际上只需要当前的 reward 加上下一个状态的值函数就OK了。
至于下一个状态的值函数怎么求，通过状态转移矩阵，求期望的可以了：
贝尔曼方程的矩阵形式：
简写为：
贝尔曼方程其实可以解出来的，只是需要求一个矩阵的逆，复杂度为O(
)，只适用于小的 MRP：
当然也有迭代法，如：
（1）Dynamic programming
（2）Monte-Carlo evaluation
（3）Temporal-Difference learning
这些在以后的课程都会提到。
3 Markov Decision Process（马尔科夫决策过程）
这个才是最重要的，毕竟强化学习里面是不能不考虑 agent 的动作的，所以这也就是 MDP 和 MRP 的区别，多一个 A (action)，而状态转移矩阵 p 和 reward 也多了一个a。
注意：
（1）MRP 的 reward 是进入一个状态得到的，而 MDP 的 reward 是执行一个动作得到的。
（2）MRP 的 P 是一个状态转换到另一个状态的概率，而 MDP 中的 P 是一个状态执行一个动作后转换到另一个状态的概率，因为实际应用中，由于环境的影响，执行一个动作得到的结果并不是一定的，也是以概率形式存在的。
3.1 policy
中文名曰（yue）策略函数，agent 执行什么样的 action 就是由 policy 决定的：
MDP 中策略之和当前的状态有关，与历史的状态无关。
3.2 值函数
这里有两个值函数，一个是状态值函数，一个是动作值函数，不过这里的状态值函数与 MRP 中的也有所不同，MRP 中的值函数与策略无关，完全又状态转移矩阵决定，而这里的值函数都是与策略有关的。动作值函数的意义为在某一状态，执行某一个动作，并根据当前的策略执行后续的动作，所得到的期望 return。两个值函数的定义式如下：
3.3 贝尔曼期望方程
这里与MRP那里类似，状态值函数为：
动作值函数为：
初学可能不容易理解两个函数的关系，这里 PPT 上介绍的比较好，首先是根据 q 计算 v：
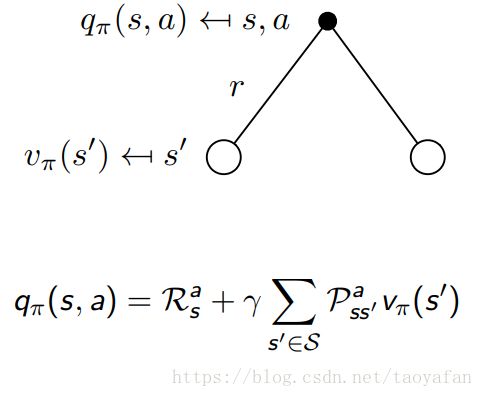
其次是根据 v 计算 q：
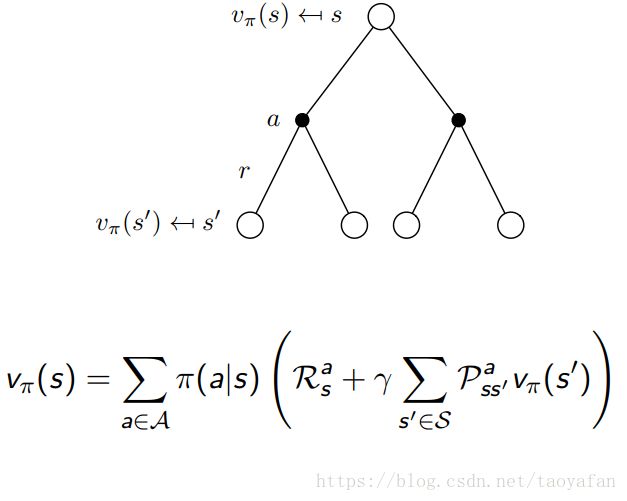
接着是根据 v 计算 v：
最后是根据 q 计算 q：
同样可以写成矩阵形式：
有代数解：
3.4 最优值函数
也就是选择最优的策略，使得值函数最大：
3.5 最优策略
策略的好坏由值函数决定，值函数越大，说明策略越好：
对于一个 MDP 存在一个（些）最优策略，比所有的其他策略都好，这些最优策略可以达到最优的状态值函数和动作值函数。
最优策略也很容易寻找，原理是找到动作 a 可以使得动作值函数最大，将这个动作的概率设为1，其他动作设为0：
3.6 贝尔曼最优方程
与贝尔曼期望方程类似，只不过不是求期望了，而是求最大值。
3.7 解贝尔曼最优方程
贝尔曼最优方程是非线性的，所以不能直接解出，有很多迭代解：
（1）Value Iteration
（2）Policy Iteration
（3）Q-learning
（4）Sarsa
4 扩展
4.1 POMDPs
A Partially Observable Markov Decision Process is an MDP with hidden states. It is a hidden Markov model with actions.定义如下
4.2 Belief States
没找到中文怎么翻译，姑且叫做信息状态吧，表示根据历史的观测得到当前的状态分布，历史的定义如下：
信息状态的定义如下：
