深度强化学习（5）策略梯度(Policy Gradient)

Policy Gradient

直接策略搜索方法是强化学习中一类很重要的方法。策略搜索是将策略进行参数化即${\pi }_{\theta }(s)$，利用参数化的线性或非线性函数（如神经网络）表示策略，寻找最优的参数$\theta$使得强化学习的目标——累积回报的期望$E\left[{\sum }_{t=0}^{H}R\left(s_t\right)|{\pi }_{\theta }\right]$最大。
本篇讨论的策略梯度(Policy Gradient)，它是Policy Based的强化学习方法，基于策略来学习。

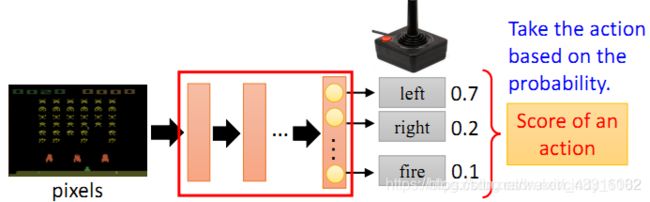
如下图所示，${\pi }_{\theta }(s)$可以理解为一个包含参数$\theta$的神经网络，该网络将观察到的变量作为模型的输入，基于概率输出对应的行动action。

从似然率的视角推导策略梯度

用$\tau$表示一组状态-行为序列$s_0,u_0,\cdots ,s_H,u_H$。
符号$R(\tau )={\sum }_{t=0}^{H}R\left(s_t,u_t\right)$表示轨迹$\tau$的回报，$P(\tau ;\theta )$表示轨迹$\tau$出现的概率；则强化学习的目标函数可表示为：

$U(\theta )=E\left({\sum }_{t=0}^{H}R\left(s_t,u_t\right);{\pi }_{\theta }\right)={\sum }_{\tau }P(\tau ;\theta )R(\tau )$

强化学习的目标是找到最优参数$\theta$,使得

${\max }_{\theta }U(\theta )={\max }_{\theta }{\sum }_{\tau }P(\tau ;\theta )R(\tau )$

这时，策略搜索方法，实际上变成了一个优化问题。我们使用最速下降法即

${\theta }_{\text{new}}={\theta }_{\text{old}}+\alpha {\nabla }_{\theta }U(\theta )$

我们对目标函数进行求导：

${\nabla }_{\theta }U(\theta )={\nabla }_{\theta }{\sum }_{\tau }P(\tau ;\theta )R(\tau )$

$={\sum }_{\tau }{\nabla }_{\theta }P(\tau ;\theta )R(\tau )$

$={\sum }_{\tau }\frac{P(\tau ;\theta )}{P(\tau ;\theta )}{\nabla }_{\theta }P(\tau ;\theta )R(\tau )$

$={\sum }_{\tau }P(\tau ;\theta )\frac{{\nabla }_{\theta }P(\tau ;\theta )R(\tau )}{P(\tau ;\theta )}$

$={\sum }_{\tau }P(\tau ;\theta ){\nabla }_{\theta }\log P(\tau ;\theta )R(\tau )$

最终策略梯度变成了求${\nabla }_{\theta }\log P(\tau ;\theta )R(\tau )$的期望。我们可以利用经验平均来进行估算。因此，当利用当前策略$\pi \theta$采样m条轨迹后，可以利用这m条轨迹的经验平均对策略梯度进行逼近：

${\nabla }_{\theta }U(\theta )\approx \hat{g}=\frac{1}{m}{\sum }_{i=1}^m{\nabla }_{\theta }\log P(\tau ;\theta )R(\tau )$

其中第一项${\nabla }_{\theta }\log P\left(\tau ;\theta \right)$ 是轨迹$\tau$的概率随参数$\theta$变化最大的方向，即最陡的方向。参数在该方向进行更新时，若沿着正方向，则该轨迹$\tau$的概率会变大，而沿着负方向进行更新时，该轨迹$\tau$的概率会变小。
再看第二项$R\left(\tau \right)$，该项控制了参数更新的方向和步长。 $R\left(\tau \right)$为正且越大则参数更新后该轨迹的概率越;$R\left(\tau \right)$为负，则降低该轨迹的概率，抑制该轨迹的发生。
因此，策略梯度从直观上进行理解时，我们发现策略梯度会增加高回报路径的概率，减小低回报路径的概率。
现在，我们解决如何求似然率的梯度：${\nabla }_{\theta }\log P\left(\tau ;\theta \right)\text{？}$
已知$\tau =s_0,u_0,\cdots ,s_H,u_H$，则轨迹的似然率可写为：

$P\left({\tau }^{\left(i\right)};\theta \right)={\prod }_{t=0}^{H}P\left(s_{t+1}^{\left(i\right)}|s_t^{\left(i\right)},u_t^{\left(i\right)}\right)\cdot {\pi }_{\theta }\left(u_t^{\left(i\right)}|s_t^{\left(i\right)}\right)$

式中，$P\left(s_{t+1}^{\left(i\right)}|s_t^{\left(i\right)},u_t^{\left(i\right)}\right)$表示动力学，式中无参数$\theta$，因此可在求导过程中消掉。具体推导如下：

${\nabla }_{\theta }\log P\left({\tau }^{(i)};\theta \right)={\nabla }_{\theta }\log \left[{\prod }_{t=0}^{H}P\left(s_{t+1}^{(i)}|s_t^{(i)},u_t^{(i)}\right)\cdot {\pi }_{\theta }\left(u_t^{(i)}|s_t^{(i)}\right)\right]$

$={\nabla }_{\theta }\left[{\sum }_{t=0}^H\log P\left(s_{t+1}^{(i)}|s_t^{(i)},u_t^{(i)}\right)+{\sum }_{t=0}^H\log {\pi }_{\theta }\left(u_t^{(i)}|s_t^{(i)}\right)\right]$

$={\nabla }_{\theta }\left[{\sum }_{t=0}^H\log {\pi }_{\theta }\left(u_t^{(i)}|s_t^{(i)}\right)\right]$

$={\sum }_{t=0}^H{\nabla }_{\theta }\log {\pi }_{\theta }\left(u_t^{(i)}|s_t^{(i)}\right)$

从上式的结果来看，似然率梯度转化为动作策略的梯度，与动力学无关。
由此，推导出了策略梯度的计算公式：

${\nabla }_{\theta }U\left(\theta \right)\approx \hat{g}=\frac{1}{m}{\sum }_{i=1}^m\left({\sum }_{t=0}^H{\nabla }_{\theta }\log {\pi }_{\theta }\left(u_t^{\left(i\right)}|s_t^{\left(i\right)}\right)R\left({\tau }^{\left(i\right)}\right)\right)$

上式给出的策略梯度是无偏的，但是方差很大。

Tip(1) 添加基线
我们在回报中引入常数基线（baseline）b来减小方差。引入基线后，策略梯度公式变为：

${\nabla }_{\theta }U\left(\theta \right)\approx \frac{1}{m}{\sum }_{i=1}^m\left({\sum }_{t=0}^H{\nabla }_{\theta }\log {\pi }_{\theta }\left(u_t^{\left(i\right)}|s_t^{\left(i\right)}\right)\left(R\left({\tau }^{\left(i\right)}\right)-b\right)\right)$

对基线的理解：
我们在训练时，总是希望当reward为正时，增大采取该行动的概率；当reward为负时，减小采取该行动的概率。在实际环境里（如游戏），有时reward总为正，在理想情况下（每个行动都会被采样到）是可以的。但训练过程中采样是随机的，可能会出现某个较好行动不被采样的情况，这会导致采取该行动的概率下降，而较差行动的概率相对上升。因此需要引入一个基线 b 。

Tip(2) 进一步考虑各个时间点的累积收益计算方式
考虑到在时间t采取的行动action与t时期之前的收益reward无关，因此只需要将t时刻开始到结束的reward进行加总。并且，由于行动action对随后各时间点的reward的影响会随着时间的推移而减小，因此加入折旧因子$\gamma$ 。

$R\left({\tau }^{\left(i\right)}\right)$ $\to$ ${\sum }_{t^{\prime }=t}^H{r}_{t^{\prime }}^{}$$\to$ ${\sum }_{t^{\prime }=t}^H{\gamma }^{t^{\prime }-t}{r}_{t^{\prime }}^{}$ ($\gamma <1$)

策略梯度公式变为：

${\nabla }_{\theta }U\left(\theta \right)\approx \frac{1}{m}{\sum }_{i=1}^m\left({\sum }_{t=0}^H{\nabla }_{\theta }\log {\pi }_{\theta }\left(u_t^{\left(i\right)}|s_t^{\left(i\right)}\right)\left({\sum }_{t^{\prime }=t}^H{\gamma }^{t^{\prime }-t}{r}_{t^{\prime }}^{}-b\right)\right)$

参考文献：
[1]https://zhuanlan.zhihu.com/p/26174099
[2]https://blog.csdn.net/cindy_1102/article/details/87905272#Policy_Gradient_9