深度增强学习（DRL）简单梳理

作者：xg123321123 - 时光杂货店

出处：http://blog.csdn.net/xg123321123/article/details/77504032

声明：版权所有，转载请联系作者并注明出处

0 主要话题

• 增强学习面临的问题
• 马尔科夫过程
• 形式化描述增强学习
• Q-learning
• 深度增强学习

1 一个简单的增强学习情景

以打砖块游戏为例，玩家需要左右移动屏幕底部的木板，将球接住并弹回到屏幕上半部分，当球触碰到一个砖块，砖块就会消失，玩家的得分就会上升 - 也就得到了reward。

如果想要让神经网络学着玩这个游戏。网络输入将会是屏幕图片，网络输出将会是三个动作：左移，右移，发射(球)。我们可以将其视为一个分类问题 - 每一帧画面，我们都必须做出决定：左移，右移还是发射。

尽管听起来比较简单，但我们需要大量的训练数据。当然，我们可以通过记录职业玩家的玩法来获得训练数据，但那不是机器真正该有的学习方式。

我们不需要谁成千上万次地来告诉机器每一帧的动作该怎么决定，我们所需要的仅仅是让机器在做了正确的决定后获得适当的反馈(reward), 然后让机器自己去领悟其余的东西。

这就是强化学习尽力在完成的任务。强化学习的地位处于监督学习和无监督学习之间。尽管监督学习给每条训练数据都标注了类别，而无监督学习什么类别也没标注，但是强化学习却给了稀疏的并且时间上有延迟的标注 - 奖励反馈(reward)。全靠这些奖励反馈，强化学习中的agent才能学习如何在环境中行动。

尽管这种思想比较符合咱们的直觉，但是实践中还是面临着许多挑战。还是拿打砖块游戏举例，当机器打掉了一块转，然后得分增加了，这常常与得分以前的最后几个动作没啥关系，而是与很多步以前的动作(比如你调整底部挡板的位置的动作)有更大的关系。

这个问题叫credit assignment problem(信用分配问题?) - 要确定某次得分与之前哪些动作有较为直接的关系，是一个比较难的问题。

一旦机器找到了一种获得奖励反馈的策略以后，是应该一直坚持它还是尝试一些别的路子来获得更大的奖励反馈呢？

这个问题叫explore-exploit dilemma(探索-开发困境) - 要一直采用已知的可行策略还是探索一些新的可能会更好的策略呢？

强化学习是动物学习过程中所采用的一种重要模型：爸妈的表扬，学校的成绩，工作中的薪水 - 这些都是奖励反馈的实例。

信用分配问题和探索-开发困境也都是我们每天都面临着的问题，这也是为什么要探索强化学习的原因；在这个探索过程中，游戏为我们提供了一个很棒的找到新方法的沙盒世界。

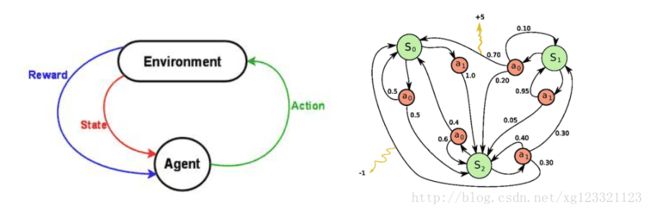
2 马尔科夫过程

现在我们的问题是该如何形式化一个强化学习的问题，最常用的方法将其表述为一个马尔科夫过程。

假如(你可以脑补打砖块游戏)环境中有一个agent能执行某些特定操作(i.e.左移木板，右移木板，发射球)，这些操作有时(当游戏处于某些特定状态)能给agent带来奖励反馈；每个操作都会改变这个环境，并将环境带入一个新的状态；在新的状态中，agent又将继续执行操作，以此类推下去。

在此过程中，agent在选择操作时所形成的规律/准则就叫策略(policy)；环境是随机的，这也意味着操作执行后到达的下一个状态也是随机的。

马尔科夫决策过程就是这三者组成：1) 环境可能出现的状态(state)，2) agent所能执行的操作(action)以及3) 指导在所有状态下具体该如何执行操作的策略(policy)。

一段完整的马尔科夫过程会形成一段状态，动作和奖励反馈所构成的有限序列。

上图中 si 表示状态， ai 表示操作， ri+1 表示操作执行后得到的奖励反馈。 sn 是这段马尔科夫过程的结束状态。值得一提的是，马尔科夫过程有一个假设前提： si+1 仅仅由 si 和 ai 联合决定，之前的状态和动作则完全不起作用。

3 折扣未来奖励 Discounted Future Reward

为了在长期过程中得到最优的结果，我们不仅需要考虑即时的奖励反馈，也需要把未来的奖励反馈纳入考虑。

对于一段马尔科夫决策过程，整个过程中的反馈奖励用以下等式表示：

R=r1+r2+...+rn

基于整个等式，从 t 时刻到最终状态所得到的全部奖励反馈可以用以下等式表示：

Rt=rt+rt+1+...+rn

但环境是随机的，我们就没法确定当我们下次做同样动作时是否还能得到同样的奖励反馈。而我们越接近未来，就越能确定未来，所以取而代之，我们采用折扣未来奖励这种做法(discounted future reward)：

Rt=rt+γrt+1+γ2rt+2+...+γn−trn

上式中， γ 是0和1之间的折扣因子 - 越接近未来的奖励反馈，对 t 时刻的奖励反馈的影响越小。可以看出， t 时刻的折扣未来奖励可以由 t+1 时刻改写出来：

Rt=rt+γ(rt+1+γ(rt+2+...))=rt+γRt+1

如果我们将 γ 设为0，那么得到的策略将非常“短视”，因为我们只考虑即时的奖励反馈。如果我们想要在即时奖励反馈和未来奖励反馈这两者间取得平衡，那么我们就应该将γ因子设为0.9之类的。当然，如果环境是确定的，所有同样的动作总是能导致同样的奖励反馈，那就可以把γ设为1了。

总的来说，一个好的策略总是能帮助agent获得最多的未来奖励反馈。

4 价值函数 Value function

除非整个过程结束，否则我们无法得到每个状态对应的奖励反馈；因此，引入了价值函数Value Function, v(s) 来表示某个状态未来的潜在价值。

从定义上看，价值函数就是回报的期望：

v(s)=E[Rt|St=s]

有了价值函数，就有三种方法获取最优的策略Policy：

• 直接优化策略 π(a|s) 或者 a=π(s) 使得回报更高
• 通过估计价值函数来间接得到优化的策略 - 既然知道每一种状态的优劣，那么就知道应该怎么选择了，而这种选择就是策略 - DQN就是通过估计价值函数来实现的
• 第三种做法是融合上面的两种方法的actor-critic算法

5 贝尔曼方程 Bellman Equation

在折扣未来奖励话题中，将 t 时刻的奖励反馈 R 定义为

Rt=rt+γ(rt+1+γ(rt+2+...))=rt+γRt+1

在价值函数话题中，将价值函数 v(s) 定义为

v(s)=E[Rt|St=s]

两个式子结合后，可以得到

v(s)=E[rt+γRt+1|St=s]

=E[rt+γv(St+1)|St=s]

上面这个公式就是贝尔曼方程的基本形态 - 它表明当前状态的奖励反馈由当前的奖励反馈和下一步的奖励反馈决定。

同时，它也表明价值函数是可以通过迭代来计算得出的。

6 动作值函数 Action-Value function

由于每个状态之后有多种动作可以选择，每个动作之后的状态又不一样，实际情况中，我们更关心在某个状态下的不同动作的价值，这就是动作值函数 Qπ(s,a) 。

因为知道了某个状态下每个动作的价值，那么就可以选择价值最大的一个动作去执行了。

跟价值函数一样，动作值函数也是用奖励反馈来表示，但动作值函数的奖励反馈和价值函数的奖励反馈不一样：动作值函数是执行完动作 at 之后得到的奖励反馈，价值函数是多种动作对应的奖励反馈的期望值。

显然，动作值函数更直观，也更容易理解。

有了上面的定义，动作值函数可以表示为：

Qπ(s,a)=E[rt+1+λrt+2+λ2rt+3+...|s,a]=Es′[r+λQπ(s′,a′)|s,a]

注：动作值函数加了 π 意味着在策略 π 下的动作价值，如果定义 vπ(s) 则表示在策略 π 下的价值函数。

能计算动作值函数还不够，因为我们需要的是最优策略 - 这可以由动作值函数来得到。

最优动作值函数和一般动作值函数的关系：

Q∗(s,a)=maxπQπ(s,a)

也就是说，最优动作值函数就是所有策略下的动作值函数的最大值。

这样的定义能让最优的动作价值具有唯一性，从而可以求解整个MDP。

那么套用上一节得到的value function，可以得到

Q∗(s,a)=Es′[r+λmaxa′Q∗(s′,a′)|s,a]

因为最优的Q值必然为最大值，所以，等式右侧的Q值必然为使a′取最大的Q值。

下面介绍基于Bellman方程的两个最基本的算法，策略迭代和值迭代。

策略迭代 Policy Iteration

值迭代 Value Iteration

7 Q-learning

Q-Learning的思想根据值迭代得到。

值迭代每次都对所有的Q值更新一遍，也就是所有的状态和动作。但在实际情况下我们没办法遍历所有的状态和动作，我们只能得到有限的系列样本。

因此，只能使用有限的样本进行操作。

在Q-learning中，我们定义了函数 Q(s,a) ，用以表示在 s 状态执行 a 操作时所能得到的最大的折扣未来奖励反馈。

Q(st,at)=maxRt+1

关于 Q(s,a) ，可以描述为在状态 s 执行动作 a 后，在游戏结束时得到的最好分数。之所以叫Q函数，因为它指代的是“某个状态下执行某个动作”的这个决定的质量如何。

如果我们仅仅知道当前状态和动作，不知道那之后的一系列状态和动作集合，我们没办法评估出当前动作的最终得分。我们能做的，仅仅是假设“Q函数是存在的”。(=，=???)

当我们在玩游戏时，面临该执行A还是B操作，如果我们有一个Q函数，那我们会直接执行最高Q值的操作。

π(s)=argmaxaQ(s,a)

其中 π 代表策略，指导agent在某种状态下如何选择action。

现在问题转化为了如何找出Q函数。

先来看这个转移动作 <s,a,r,s′> ，正如之前提到的折扣未来奖励反馈一样，我们能用状态 s 和动作 a 的Q值来表示下一个状态 s′ 的Q值：

Q(s,a)=r+γmaxa′Q(s′,a′)

上式是Bellman 方程：当前状态下当前动作的最大未来奖励反馈等于当前动作的即时奖励反馈+下一状态的最大未来奖励反馈。(有点像踢皮球？现在搞不定的，就留给以后来解决。其实是动态规划…)

Q-learning的核心思想是通过Bellman方程来迭代逼近Q函数：

Q(St,At)←Q(St,At)+α(Rt+1+λmaxaQ(St+1,a)−Q(St,At))

虽然根据值迭代来计算出target Q值，但是这里并没有直接将这个Q值(估计出来的)直接赋予新的Q，而是采用渐进的方式类似梯度下降，朝target迈近一小步，取决于α,这就能够减少估计误差造成的影响。类似随机梯度下降，最后可以收敛到最优的Q值。

具体的算法如下：

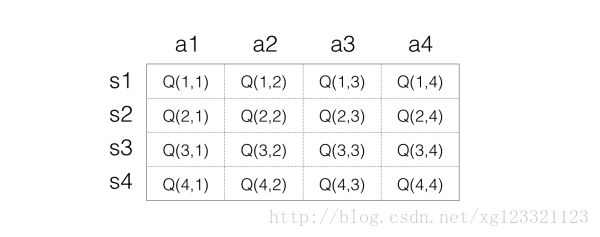
最简单地，Q函数可以用一张表格来实现，表格的行头为状态，列头为动作。Q-learning算法可以见以下：

算法中的 α 是学习率，用以新得到的Q值能多大程度地修改以往的Q值，当 α =1,等式就和Bellman方程一样了。

等式中我们用来更新 Q[St,At] 的 maxaQ[st+1,a] 只是一种近似，甚至在学习的早期阶段，很可能完全就是错的。当随着迭代次数的上升，这种逼近会越来越准确，以至于当迭代到一定次数时，Q函数会收敛，并且反映出真正的Q值。

举个栗子：

为了得到最优策略Policy，我们会估算每一个状态下的每一种动作的价值Value。同时，每一个时间点的Q(s,a)和当前得到的Reward以及下一个时间点的Q(s,a)有关。

但是在实验中，只可能知道当前时刻的Q值，怎么知道下一个时刻的Q值呢？

Q-Learning建立在虚拟环境下无限次的实验。

这意味着可以把上一次实验计算得到的Q值拿来使用。这样就可以根据当前的Reward及上一次实验中记录的下一个时间片的Q值来更新当前的Q值了。

首先确定存储Q值的方式 - 最简单的想法是用矩阵，一个s一个a对应一个Q值，所以可以把Q值想象为一个很大的表格，横列代表s，纵列代表a，里面的数字代表Q值，如下表示：

接下来进行反复实验以更新表格。

Step 1：初始化Q矩阵，比如都设置为0.

Step 2：开始实验。根据当前Q矩阵及 ϵ−greedy 方法获取动作。比如当前处在状态s1，那么在s1一列每一个Q值都是0，那么这个时候随便选择都可以。

假设选择a2动作，然后得到的reward是1，并且进入到s3状态，接下来要根据以下等式更新来Q值：

Q(St,At)←Q(St,At)+α(Rt+1+λmaxaQ(St+1,a)−Q(St,At))

假设 α 是1， λ 也等于1，也就是每一次都把目标Q值赋给Q。那么这里公式变成：

Q(St,At)=Rt+1+maxaQ(St+1,a)

将此处的状态带入，得到

Q(s1,a2)=1+maxaQ(s3,a)

注意：此时s3状态对应的各个动作，回报值最大为0，所以 Q(s1,a2)=1+0=1 ,Q表格就变成：

Step 3：接下来进入下一次动作，现在处于状态s3，假设选择动作a3，然后得到1的reward，状态变成s1，此时s1状态对应的各个动作，回报值最大为0，那么我们同样进行更新：

Q(s3,a3)=2+maxaQ(s1,a)=2+1=3

所以Q的表格就变成：

Step 4： 反复进行上面的步骤，Q值也就在实验进行的同时反复更新。直到最后收敛。

8 Deep Q Network

打砖块游戏中，环境能够用木板的位置，球的位置和方向以及所有砖块的位置来定义。这种符合直觉的表征方式会随着游戏的改变而不再适用。如果想要找到更加通用的表征方式呢？

那就是屏幕像素。屏幕像素隐含着游戏中的所有相关信息，包括(打砖块中的)球的速度和方向等等(可以通过2张连续的帧计算出来)。

如果要应用DeepMind在论文《Human-level_control_through_deep_reinforcement_learning》中的预处理手段：取当前帧向前推4步得到的连续4帧，resize为84*84大小，转化为256阶的灰度图 - 这种方式下的打砖块游戏有 25684×84×4≈1067970 种可能的游戏状态。

这时的Q表格中就有 1067970 行 - 比已知宇宙中的原子数目还多。尽管在这之中，有些状态并不会出现，这会是一张稀疏表格。很多状态几乎就不会被触发，即使如此，也要花费宇宙生命那么长的时间来使Q表格收敛，这被称为维度灾难(curse of dimensionality)。

那么，如果能够对之前没有出现过的一些状态的Q值进行近似猜测就很棒了。

简单来说，就是用一个函数来表示Q(s,a)：

Q(s,a)=f(s,a)

f 可以是任意类型的函数，如线性函数：

Q(s,a)=w1s+w2a+b

其中 w1,w2,b 是函数 f 的参数，通过函数表示，无所谓 s 到底是多大的维度，最后都能通过矩阵运算降维输出为单值的Q。

这是函数近似的基本思路。

如果我们就用 w 来统一表示函数f的参数，那么就有

Q(s,a)=f(s,a,w)

之所以叫作近似，是因为我们并不知道Q值的实际分布情况，本质上是用一个函数来近似Q值的分布，所以也可以说是

Q(s,a)≈f(s,a,w)

而这就是深度学习的切入点。

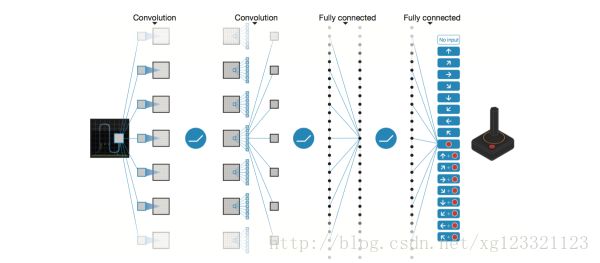
神经网络能够将高度结构化数据的特征提取出来。那我们可以将Q函数用神经网络的形式表征出来 - 以状态和动作为输入，然后输出相应的Q值。或者我们可以仅仅将状态作为输入，然后输出可能发生的每个动作的Q值。

这种思路的优点在于，如果我们想执行Q值更新或者执行具有最高Q值的操作的话，只需要做一次网络前传，然后就能立即得到所有可能动作的Q值了。

对于Atari游戏而言，这是一个高维状态输入(原始图像)，低维动作输出(几个离散的动作，比如上下左右)的过程。在表示函数时，我们只需要对高维状态进行降维，而不需要对动作也进行降维处理。

Q(s)≈f(s,w) ，只把状态s作为输入，但是输出的时候输出每一个动作的Q值，也就是输出一个向量 [Q(s,a1),Q(s,a2),Q(s,a3),...,Q(s,an)] ，这里的输出是一个包含了所有动作的Q值的向量。只要输入状态s，同时可以得到所有的动作Q值，可以更方便的进行Q-Learning中动作的选择与Q值更新。

Left: Naive formulation of deep Q-network. Right: More optimized architecture of deep Q-network, used in DeepMind paper.

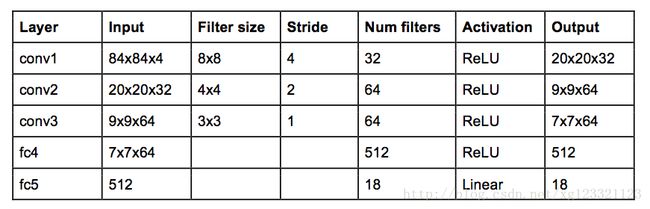
DeepMind在上面那篇论文中用的网络结构如下：

这就是传统的CNN结构，但是没pooling层 - pooling层的平移不变特性将会让网络对图片中物体的位置改变不再敏感 - 而(打砖块)游戏中，球的位置是对于奖励反馈的确定是十分重要的，所以不能有pooling层。

网络输入为4张连续的84*84的游戏画面灰度图，网络输出为每个可能动作的Q值，Q值可以为任何实数值，这就转化成了回归任务，可以用平方差loss进行优化。

神经网络的训练是一个最优化问题，最优化某个损失函数loss function，也就是标签和网络输出的偏差，目标是让损失函数最小化。为此，我们需要有样本，巨量的有标签数据，然后通过反向传播使用梯度下降的方法来更新神经网络的参数。

所以要训练Q网络，我们要能够为Q网络提供有标签的样本。

如何为Q网络提供有标签的样本？

答案就是Q-Learning算法。

回忆Q-Learning算法，Q值的更新依靠的是利用Reward和Q计算出来的目标Q值：

Rt+1+λmaxaQ(St+1,a)

因此，我们可以把target Q值作为标签，我们的目标就是让Q值趋近于target Q值。

因此，Q网络训练的损失函数就是

上面公式是 s‘,a‘ 即下一个状态和动作。

考虑一个转移动作 <s,a,r,s′> ，以前的算法中的Q值更新规则需要做以下调整：

• 当前状态 s 在网络中进行前传后，得到所有可能动作的Q值预测；
• 下一状态 s′ 在网络中进行前传后，计算所有输出中最大值 maxa′Q(s′,a′) ;
• 将动作的目标Q值表示为 r+γmaxa′Q(s′,a′) (即上一步中计算出来的最大值)，同时将其他动作的目标Q值设为和第一步中返回的值相等，让所有的输出的误差为0；
• 用反向传播进行网络权重更新

既然确定了损失函数，即cost，也确定了获取样本的方法。那么DQN的整个算法也就成型了！

9 经验重放 Experience Replay

目前为止，我们大概知道了如何用Q-learning和CNN的近似Q函数来评估每个状态的未来奖励反馈，然而实验表明，非线性函数的Q值逼近非常不稳定，必须得用很多trick来帮助其收敛，同时耗时巨大。

Experience Replay就是这样的一种技术，在游戏数据的采集过程中，所有的经验数据 <s,a,r,s′> 都被存储到一个回放池(replay memory)中。当训练网络时，从回放池中随机地取一小撮数据，而不是最新连续的几条转换数据，进行训练。

这种方法打破了连续数据之间的关联性。由于神经网络是有监督模型，所以要求训练数据必须是独立同分布的，否则将会使得网络陷于局部最小值。

同时，这种经验回放简化了算法的调试和测试，让训练更像有监督学习。毕竟，我们可以从人类玩家那收集到这些经验数据然后用于网络训练。

10 探索-开发 Exploration-Exploitation

在Q-Learning算法中，需要使用某一个policy来生成动作，这个policy不是优化的那个policy，所以Q-Learning算法叫做Off-policy的算法；另一方面，因为Q-Learning完全不考虑model(就是环境的具体情况)，只考虑看到的环境及奖励反馈，因此是model-free的方法。

Q-learning尝试解决信用分配问题 - 将奖励反馈一直回传到做关键决定的时间节点，但是我们还得面临Exploration-Exploitation困境。

在Q-Learning中，我们需要根据哪种policy来生成action呢？有两种做法：

• 随机的生成一个动作

• 根据当前的Q值计算出一个最优的动作，这个策略 π 称之为greedy policy贪婪策略。也就是
  

  π(St+1)=argmaxaQ(St+1,a)

使用随机的动作就是exploration，也就是探索未知的动作会产生的效果，有利于更新Q值，获得更好的policy。而使用greedy policy也就是target policy则是exploitation，利用policy，相对来说就不好更新出更好的Q值，但可以得到更好的测试效果用于判断算法是否有效。

将两者结合起来就是所谓的 ε−greedy 探索 - 设置因子 ε ，每次执行动作时，有ε的几率执行随机动作(剩下1-ε的几率执行具有最高Q值的动作)。DeepMind实际上让ε随着时间从1逐渐减少到0.1 - 最开始时，agent执行完全随机的动作，以此探索最大化的状态空间，然后逐渐将“探索”降至一个固定的频率。可以更改\epsilon的值从而得到不同的exploration和exploitation的比例。

这里需要说明的一点是使用\epsilon-greedy策略是一种极其简单粗暴的方法，对于一些复杂的任务采用这种方法来探索未知空间是不可取的。因此，最近有越来越多的方法来改进这种探索机制。

11 DQN训练

以下就是带有经验回放的最终的深度强化学习算法：

两种表述方式，自取。

算法看起来很长，其实就是在反复试验，然后存储数据。当数据存到一定程度，就每次随机采用数据，进行梯度下降。

在DQN中增强学习Q-Learning算法和深度学习的SGD训练是同步进行的，通过Q-Learning获取无限量的训练样本，然后对神经网络进行训练。

而样本的获取关键是计算y，也就是标签。

当然，DeepMind实际过程中还运用了很多其他的trick来让算法更有效(target network, error clipping, reward clipping 等等)

深度强化学习算法的惊艳点在于，它能学习任何东西。Q函数最初是随机的，最初的决策也基本就是“垃圾输出”；然后我们不断地利用它的“垃圾输出”进行网络的更新，再适时辅以奖励反馈，最后它就学会了这一切？？

更进一步

12 on-policy vs. off-policy

这是强化学习中的一种方法划分方式。

估计policy(value-function)的时候，需要用到一些样本，这些样本也需要采用某种策略(可能固定、可能完全随机、也可能隔一段时间调整一次)生成的。
而判断on-policy和off-policy的关键在于，你所估计的policy(value-function) 和 生成样本所采用的policy 是不是一样的。如果一样，那就是on-policy的，否则是off-policy的。

• on-policy: 生成样本的policy跟网络更新参数时使用的policy相同。

  • 典型为SARAS算法，执行两次动作得到(s,a,r,s’,a’)才可以更新一次；而且a’是在特定π的指导下执行的动作，因此估计出来的Q(s,a)是在该π之下的Q-value，即Q_π(s,a)，因此生成样本的policy和学习时的policy相同，算法为on-policy算法。该方法会遭遇探索-开发的矛盾，只利用目前已知的最优选择，可能学不到最优解，收敛到局部最优，而加入探索又降低了学习效率。epsilon-greedy 算法是这种矛盾的折衷。优点是直接了当，速度快，劣势是不一定找到最优策略。

• off-policy：生成样本的policy跟网络更新参数时使用的policy不同。

  • 典型为Q-learning算法，每次只需要执行一次动作得到(s,a,r,s’)就可以更新一次；因为a’永远是最优的那个action，因此你估计的策略应该是最优的，即Q_π*(s,a)，而你生成样本时用的策略则不一定是最优的，因此这里生成样本的policy和学习时的policy不同，为off-policy算法。先产生某概率分布下的大量行为数据(behavior policy)，意在探索。从这些偏离最优策略的数据中寻求target policy。当然这么做是需要满足数学条件的：假設π是目标策略, µ是行为策略，那么从µ学到π的条件是：π(a|s) > 0 必然有 µ(a|s) > 0成立。
• 两种学习策略的关系是：on-policy是off-policy 的特殊情形，其target policy 和behavior policy是一个。劣势是曲折，收敛慢，但优势是更为强大和通用。其强大是因为它确保了数据全面性，所有行为都能覆盖。

13 model-based vs. model-free

另一种强化学习中的方法划分方式。

• Model-based: 尝试给环境建模，最终基于这个环境选择最优的策略。建模时一些微小的错误将给agent在选择动作时产生比较大的负面影响。

• Model-free: 不对环境进行建模，而是一直在每一步中去尝试学习最优的策略，在多次迭代后就得到了整个环境最优的策略(e.g. Q-learning)。

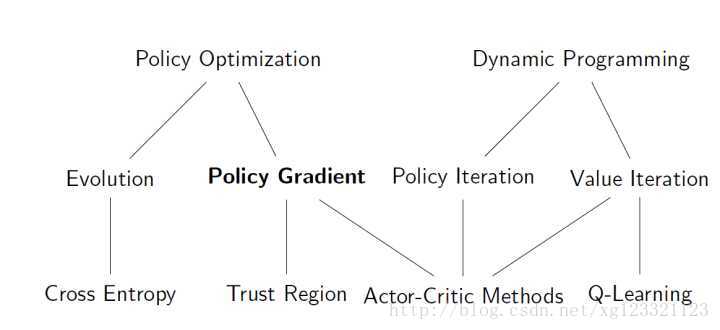
14 RL两大分支

可以看到，Q Learning 和 Policy Gradient分属RL的两大分支：Dynamic Programming 和 Policy Optimization。

上面一直都在说Q Learning，接下来讲讲Policy Gradient。

P.S. Cross Entropy Method 是较为简单且经典的Policy Optimization 算法，在一些简单场景效果很好。

15 Policy gradient

---

本篇博客主要整理自以下文章
《Guest Post (Part I): Demystifying Deep Reinforcement Learning》
《知乎专栏 - 智能单元》
强化学习中on-policy 与off-policy有什么区别？
增强学习中的on-policy和off-policy的区别
强化学习on-policy跟off-policy的区别
解释model-based和model-free，on-policy和off-policy区别？
reinforcement learning，增强学习：Integrating Learning and Planning