机器学习十大经典算法之KNN最近邻算法
KNN简介
KNN(K-NearestNeighbor)是机器学习入门级的分类算法,非常简单。它实现将距离近的样本点划为同一类别;KNN中的K指的是近邻个数,也就是最近的K个点 ;根据它距离最近的K个点是什么类别来判断属于哪个类别。
KNN算法步骤
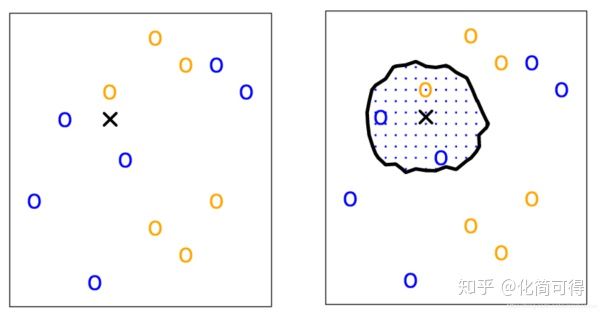
我们有一堆样本点,类别已知,如下图左,蓝色为一类,黄色为另一类。现在有个新样本点,也就是图中黑色的叉叉,需要判断它属于哪一类。
KNN做的就是选出距离目标点黑叉叉距离最近的k个点,看这k个点的大多数颜色是什么颜色。这里的距离用欧氏距离来度量。
给定两个样本 X = ( x 1 , x 2 , . . . , x n ) X=(x_{1},x_{2},...,x_{n}) X=(x1,x2,...,xn) 和 Y = ( y 1 , y 2 , . . . , y n ) Y=(y_{1},y_{2},...,y_{n}) Y=(y1,y2,...,yn) ,其中n表示特征数 ,X和Y两个向量间的欧氏距离(Euclidean Distance)表示为:
d i s t e d ( X , Y ) = ( x 1 − y 1 ) 2 + . . . + ( x n − y n ) 2 2 dist_{ed}(X,Y)=\sqrt[2]{(x_{1}-y_{1})^{2}+...+(x_{n}-y_{n})^{2}} disted(X,Y)=2(x1−y1)2+...+(xn−yn)2
当我们设定k=1时,距离目标点最近的点是黄色,就认为目标点属于黄色那类。当k设为3时,我们可以看到距离最近的三个点,有两个是蓝色,一个是黄色,因此认为目标点属于蓝色的一类。
所以,K的选择不同,得到的结果也会不同。
K值选择
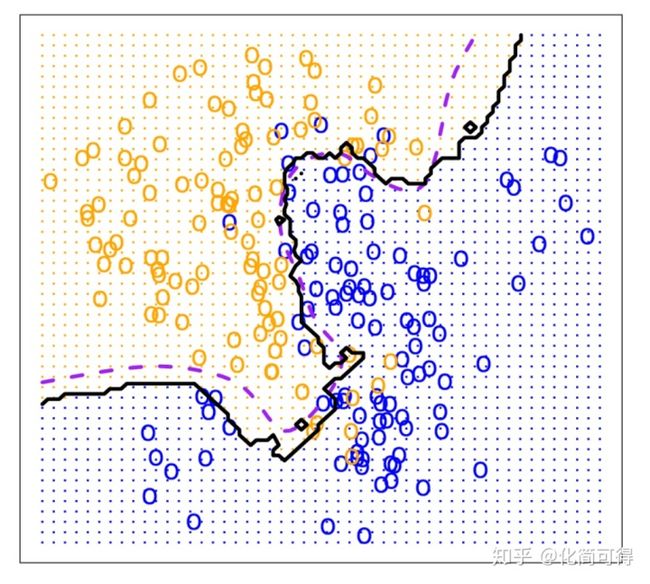
KNN的决策边界一般不是线性的,也就是说KNN是一种非线性分类器,如下图。
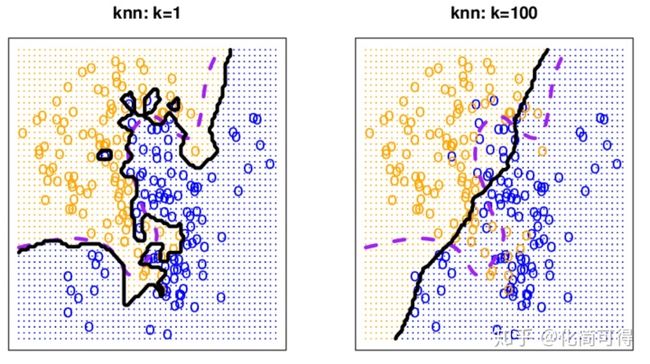
K越小越容易过拟合,当K=1时,这时只根据单个近邻进行预测,如果离目标点最近的一个点是噪声,就会出错,此时模型复杂度高,稳健性低,决策边界崎岖。
但是如果K取的过大,这时与目标点较远的样本点也会对预测起作用,就会导致欠拟合,此时模型变得简单,决策边界变平滑。
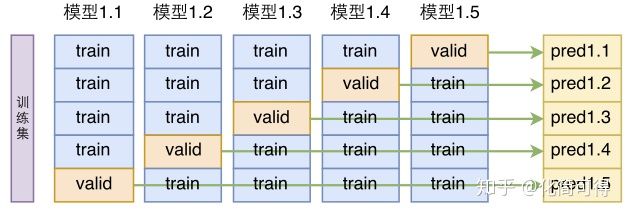
寻找最合适的K值,比较经典的方法是N折交叉验证。
上图展示的是5折交叉验证,也就是将已知样本集等分为5份,其中4份作为训练集,1份为验证集,做出5个模型。
具体过程
将样本数据按照一定比例,拆分出训练用的数据和验证用的数据,比如6:4拆分出部分训练数据和验证数据,从选取一个较小的K值开始,不断增加K的值,然后计算验证集合的方差,最终找到一个比较合适的K值。
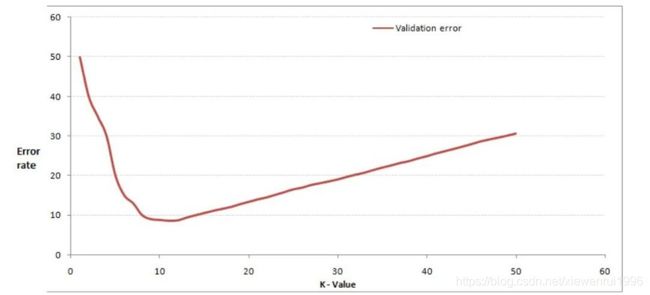
通过交叉验证计算方差后你大致会得到下面这样的图:
由上图可知,当你增大k的时候,一般错误率会先降低,因为有周围更多的样本可以借鉴了,分类效果会变好。但注意,和K-means不一样,当K值更大的时候,错误率会更高。这也很好理解,比如说你一共就35个样本,当你K增大到30的时候,KNN基本上就没意义了。
所以选择K点的时候可以选择一个较大的临界K点,当它继续增大或减小的时候,错误率都会上升,比如图中的K=10。
PS:处理数据要先对其进行标准化
X new = X − min ( X ) max ( X ) − min ( X ) X_{\text {new }}=\frac{X-\min (X)}{\max (X)-\min (X)} Xnew =max(X)−min(X)X−min(X)
也可以采用标准差标准化:
X new = X − mean ( X ) std ( X ) X_{\text {new}}=\frac{X-\operatorname{mean}(X)}{\operatorname{std}(X)} Xnew=std(X)X−mean(X)
KNN优缺点
KNN的优点在于原理简单,容易实现,对于边界不规则数据的分类效果好于线性分类器。
缺点:
- 要保存全部数据集,需要大量的存储空间;
- 需要计算每个未知点到全部已知点的距离,非常耗时;
- 对于不平衡数据效果不好,需要进行改进;
- 不适用于特征空间维度高的情况。
代码实现
伪代码
对测试样本点进行以下操作:
(1)计算已知类别数据集中的点与当前点之间的距离;
(2)按照距离递增次序排序;
(3)选取与当前点距离最小的k个点;
(4)确定前k个点所在类别的出现频率;
(5)返回前k个点出现频率最高的类别作为当前点的预测分类。
具体实现
https://github.com/GreedyAIAcademy/Machine-Learning/tree/master/2.KNN
参考文章
https://www.cnblogs.com/listenfwind/p/10311496.html