数据结构小笔记：二叉搜索树

1. 定义

定义：二叉查找树(Binary Search Tree)，又被称为二叉搜索树。设x为二叉查找树中的一个结点，x节点包含关键字key，节点x的key值记为key[x]。如果y是x的左子树中的一个 结点，则key[y] <= key[x]；如果y是x的右子树的一个结点，则key[y] >= key[x]。

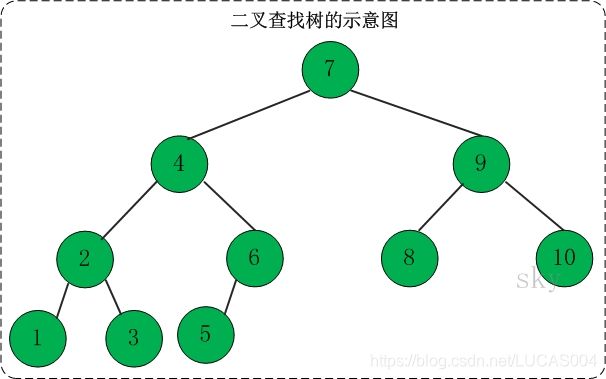
在二叉查找树中：
(01) 若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
(02) 任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
(03) 任意节点的左、右子树也分别为二叉查找树。
(04) 没有键值相等的节点（no duplicate nodes）。

2. C语言实现功能函数

queue.h

#ifndef _QUEUE_H__
#define _QUEUE_H__

#include <stdio.h>
#include <stdbool.h>
#include <stdlib.h>
#include "bintree.h"

typedef BNode* BT;
typedef struct Queue{
	BT *base;
	size_t cap;      //容量
	size_t size;     //元素的个数
	size_t first;    //队列头元素的下标位置
}Queue;

int queue_init(Queue *q,size_t cap); //初始化队列
void queue_destroy(Queue *q); //销毁队列
bool queue_is_empty(Queue *q); //判断队列是否为空
bool queue_is_full(Queue *q); //判断队列是否满
void queue_clear(Queue *q); //清空队列
void queue_push(Queue *q,BT data); //向队列中压入一个元素
BT queue_pop(Queue *q); //从队列中弹出一个元素
BT queue_peek_front(Queue *q); //查看队列中的第一个元素
BT queue_peek_back(Queue *q); //查看队列中的最后一个元素
void queue_foreach(Queue *q,void (*foreach)(BT)); //遍历队列中的元素

#endif //_QUEUE_H__

queue.c

#include "queue.h"
int queue_init(Queue *q,size_t cap){
	q->base = calloc(cap,sizeof(BT));
	if(q->base == NULL){
		return -1;	
	}
	q->cap = cap;
	q->size = 0;
	q->first = 0;
	return 0;
}
void queue_destroy(Queue *q){
	if(q->base){
		free(q->base);
	}	
	q->base = NULL;
}
bool queue_is_empty(Queue *q){
	return q->size == 0;	
}
bool queue_is_full(Queue *q){
	return q->size == q->cap;	
}
void queue_clear(Queue *q){
	q->size = 0;
	q->first = 0;
}
void queue_push(Queue *q,BT data){
	q->base[(q->size+q->first)%q->cap] = data;	
	++q->size;
}
BT queue_pop(Queue *q){
	BT data = q->base[q->first];	
	q->first = (q->first+1)%q->cap;
	--q->size;
	return data;
}
BT queue_peek_front(Queue *q){
	return q->base[q->first];	
}
BT queue_peek_back(Queue *q){
	return q->base[(q->size+q->first-1)%q->cap];	
}
void queue_foreach(Queue *q,void (*foreach)(BT)){
	int i;
	for(i=0;i<q->size;i++){
		foreach(q->base[(i+q->first)%q->cap]);	
	}
}

stack.h

#ifndef _STACK_H__
#define _STACK_H__

#include <stdlib.h>
#include <stdbool.h>
#include <stdio.h>
#include "bintree.h"

//typedef int T;
typedef BNode * ST;
typedef struct Stack{
	ST *base;          //内存
	size_t cap;       //容量
	size_t size;      //元素个数
}Stack;

int stack_init(Stack *s,size_t cap); //初始化堆栈
void stack_destroy(Stack *s); //销毁堆栈
bool stack_is_empty(Stack *s); //判断堆栈是否为空
bool stack_is_full(Stack *s); //判断堆栈是否满
void stack_push(Stack *s,ST data); //往堆栈中压入一个元素
void stack_clear(Stack *s); //清空堆栈
ST stack_pop(Stack *s); //从堆栈中弹出一个元素
ST stack_top(Stack *s); //查看堆栈的栈顶元素
void stack_foreach(Stack *s,void (*foreach)(ST)); //遍历堆栈中的元素
bool is_stack_out(ST in[],ST out[],size_t n); //判断传过来的数组是否符合出栈顺序

#endif //_STACK_H__

stack.c

#include "stack.h"

int stack_init(Stack *s,size_t cap){
	s->base = calloc(cap,sizeof(ST));
	s->cap = cap;
	s->size = 0;
}
void stack_destroy(Stack *s){
	if(s->base)
		free(s->base);
	s->base = NULL;
}
bool stack_is_empty(Stack *s){
	return s->size == 0;	
}
bool stack_is_full(Stack *s){
	return s->size == s->cap;	
}
void stack_clear(Stack *s){
	s->size = 0;	
}
void stack_push(Stack *s,ST data){
	s->base[s->size++] = data;	
}
ST stack_pop(Stack *s){
	return s->base[--s->size];	
}
ST stack_top(Stack *s){
	return s->base[s->size-1];	
}
void stack_foreach(Stack *s,void (*foreach)(ST)){
	int i;
	for(i=0;i<s->size;i++){
		foreach(s->base[i]);	
	}
}
//in  1 2 3 4 5 
//out 1 2 3 4 5  true
//out 2 1 3 4 5  true   
//out 4 3 5 2 1  true
//out 1 3 4 2 5  true
//out 4 1 3 2 5  false
bool is_stack_out(ST in[],ST out[],size_t n){
	Stack s;
	stack_init(&s,n);
	int i=0,j=0;
	for(i=0;i<n;i++){
		stack_push(&s,in[i]);//压一个元素到栈里面
		while((!stack_is_empty(&s))&&stack_top(&s)==out[j]){
			stack_pop(&s);
			++j;
		}
	}
	bool ret = stack_is_empty(&s);
	stack_destroy(&s);
	return ret;
}

#ifndef _BIN_TREE_H__
#define _BIN_TREE_H__

#include <stdbool.h>
#include <stdlib.h>
#include <stdio.h>

typedef int T;
typedef struct BNode{
	T data;
	struct BNode *left;
	struct BNode *right;
}BNode;

typedef BNode *  BTree;
//树的根节点是存储数据的  如果根节点不存在则树为空 
//判断树是否为空的条件是判断根节点是否存在 
//表示一棵树 只需要记录根节点即可
//BTree tree = NULL;
bool btree_is_empty(BTree tree); //判断二叉搜索树是否为空
size_t btree_size(BTree tree); //计算二叉搜索树的个数
size_t btree_height(BTree tree); //计算二叉搜索树的高度
void btree_clear(BTree *ptree); //清空二叉搜索树
int btree_search(BTree tree,T data,int (*compare)(T,T)); //在二叉搜索树中查找元素
int btree_insert(BTree *ptree,T data,int (*compare)(T,T)); //在二叉搜索树中插入一个元素
int btree_delete(BTree *ptree,T data,int (*compare)(T,T)); //在二叉搜索树中删除一个元素
void btree_foreach_prev(BTree tree,void (*foreach)(T)); //先序遍历
void btree_foreach_mid(BTree tree,void (*foreach)(T)); //中序遍历
void btree_foreach_last(BTree tree,void (*foreach)(T)); //后序遍历
void btree_foreach_prev2(BTree tree,void (*foreach)(T)); //先序遍历
void btree_foreach_mid2(BTree tree,void (*foreach)(T)); //中序遍历
void btree_foreach_last2(BTree tree,void (*foreach)(T)); //后序遍历
void btree_foreach_layer(BTree tree,void (*foreach)(T)); //层序遍历
bool btree_is_sort(BTree tree); //判断该二叉树是否为二叉搜索树
bool arr_is_last_btree(T arr[],size_t n);//数组中的元素是否可能是有序二叉树后序遍历的结果
bool arr_is_prev_btree(T arr[],size_t n);//数组中的元素是否可能是有序二叉树前序遍历的结果

#endif //_BIN_TREE_H__

#include "bintree.h"
#include "stack.h"
#include "queue.h"
//树的根节点是存储数据的  如果根节点不存在则树为空 
//判断树是否为空的条件是判断根节点是否存在 
//表示一棵树 只需要记录根节点即可
//BTree tree = NULL;
bool btree_is_empty(BTree tree){
	return tree == NULL;	
}
size_t btree_size(BTree tree){
	if(tree == NULL)
		return 0;
	return btree_size(tree->left) + btree_size(tree->right) + 1;
}
size_t btree_height(BTree tree){
	if(tree == NULL)
		return 0;
	size_t lh = btree_height(tree->left);
	size_t rh = btree_height(tree->right);
	return lh>rh?lh+1:rh+1;
}
void btree_clear(BTree *ptree){
	if(*ptree == NULL){
		return;
	}	
	btree_clear(&(*ptree)->left);
	btree_clear(&(*ptree)->right);
	free(*ptree);
	*ptree = NULL;
}

/*  递归实现查找
int btree_search(BTree tree,T data,int (*compare)(T,T)){
	if(tree == NULL){
		return -1;	
	}	
	if(compare(tree->data,data)==0){
		return 0;	
	}else if(compare(data,tree->data)<0){
		return btree_search(tree->left,data,compare);	
	}else{
		return btree_search(tree->right,data,compare);	
	}
}
*/
int btree_search(BTree tree,T data,int (*compare)(T,T)){
	while(tree != NULL){
		if(compare(tree->data,data)==0){
			return 0;	
		}else if(compare(data,tree->data)<0){
			tree = tree->left;	
		}else{
			tree = tree->right;	
		}
	}
	return -1;
}

BNode *btree_create_tnode(T data){
	BNode *node = malloc(sizeof(BNode));
	if(node!=NULL){
		node->data = data;
		node->left = NULL;
		node->right = NULL;
	}
	return node;
}
/*  递归实现在二叉搜索树中插入元素
int btree_insert(BTree *ptree,T data,int (*compare)(T,T)){
	if(*ptree == NULL){
		*ptree = btree_create_tnode(data);
		if(*ptree == NULL)
			return -1;
		return 0;
	}	
	int ret = compare(data,(*ptree)->data);
	if(ret<0){
		return btree_insert(&(*ptree)->left,data,compare);
	}else if(ret>0){
		return btree_insert(&(*ptree)->right,data,compare);
	}else{
		return -1;
	}
}
*/
int btree_insert(BTree *ptree,T data,int (*compare)(T,T)){
	while(*ptree != NULL){
		int ret = compare(data,(*ptree)->data);
		if(ret < 0){
			ptree = &(*ptree)->left;	
		}else if(ret > 0){
			ptree = &(*ptree)->right;	
		}else{
			return -1;	
		}
	}
	*ptree = btree_create_tnode(data);
	if(*ptree == NULL)
		return -1;
	return 0;
}

/*  递归实现在二叉搜索树中删除元素
int btree_delete(BTree *ptree,T data,int (*compare)(T,T)){
	if(*ptree == NULL)
		return -1;
	
	int ret = compare(data,(*ptree)->data);
	if(ret == 0){
		BNode *node = *ptree;
		if(node->left != NULL){
			*ptree = node->left;
			if(node->right != NULL){
				while(*ptree != NULL){
					ptree = &(*ptree)->right;
				}
				*ptree = node->right;
			}
		}else{
			*ptree = node->right;	
		}
		free(node);
		return 0;
	}else if(ret < 0){
		return btree_delete(&(*ptree)->left,data,compare);
	}else{
		return btree_delete(&(*ptree)->right,data,compare);
	}
}
*/
int btree_delete(BTree *ptree,T data,int (*compare)(T,T)){
	while(*ptree!=NULL){
		int ret = compare(data,(*ptree)->data);
		if(ret == 0){
			BNode *node = *ptree;
			if(node->right != NULL){
				*ptree = node->right;
				if(node->left != NULL){
					while(*ptree != NULL){
						ptree = &(*ptree)->left;	
					}
					*ptree = node->left;
				}
			}else{
				*ptree = node->left;	
			}
			free(node);
			return 0;
		}else if(ret < 0){
			ptree = &(*ptree)->left;	
		}else{
			ptree = &(*ptree)->right;
		}
	}	
	return -1;
}

// 用非递归实现先序遍历
void btree_foreach_prev2(BTree tree,void (*foreach)(T)){
	if(tree == NULL)
		return;
	Stack s;
	stack_init(&s,btree_size(tree));
	stack_push(&s,tree);
	while(!stack_is_empty(&s)){
		BNode *node = stack_pop(&s);
		foreach(node->data);
		if(node->right!=NULL){
			stack_push(&s,node->right);	
		}
		if(node->left!=NULL){
			stack_push(&s,node->left);	
		}
	}

	stack_destroy(&s);
}
// 用非递归实现中序遍历
void btree_foreach_mid2(BTree tree,void (*foreach)(T)){
	if(tree == NULL)
		return;
	Stack s;
	stack_init(&s,btree_size(tree));
	BNode *p = tree;
	while(p!=NULL||!stack_is_empty(&s)){
		while(p!=NULL){
			stack_push(&s,p);
			p = p->left;
		}	
		if(!stack_is_empty(&s)){
			p = stack_pop(&s);
			foreach(p->data);
			p = p->right;
		}
	}
	stack_destroy(&s);
}
// 用非递归实现后序遍历
void btree_foreach_last2(BTree tree,void (*foreach)(T)){
	if(tree == NULL)
		return;
	Stack s;
	stack_init(&s,btree_size(tree));
	Stack res;
	stack_init(&res,btree_size(tree));
	stack_push(&s,tree);
	while(!stack_is_empty(&s)){
		tree = stack_pop(&s);
		stack_push(&res,tree);
		if(tree->left!=NULL){
			stack_push(&s,tree->left);	
		}
		if(tree->right!=NULL){
			stack_push(&s,tree->right);	
		}
	}
	while(!stack_is_empty(&res)){
		tree = stack_pop(&res);
		foreach(tree->data);
	}
	stack_destroy(&s);
	stack_destroy(&res);
}

//所谓的先 中 后 其实是遍历根节点的顺序
// 用递归实现先序遍历
void btree_foreach_prev(BTree tree,void (*foreach)(T)){
	if(tree != NULL){
		foreach(tree->data);
		btree_foreach_prev(tree->left,foreach);
		btree_foreach_prev(tree->right,foreach);
	}
}
// 用递归实现中序遍历
void btree_foreach_mid(BTree tree,void (*foreach)(T)){
	if(tree != NULL){
		btree_foreach_mid(tree->left,foreach);
		foreach(tree->data);
		btree_foreach_mid(tree->right,foreach);
	}
}
// 用递归实现后序遍历
void btree_foreach_last(BTree tree,void (*foreach)(T)){
	if(tree != NULL){
		btree_foreach_last(tree->left,foreach);
		btree_foreach_last(tree->right,foreach);
		foreach(tree->data);
	}
}

void btree_foreach_layer(BTree tree,void (*foreach)(T)){
	if(tree == NULL)
		return;
	Queue que;
	queue_init(&que,btree_size(tree));
	queue_push(&que,tree);
	while(!queue_is_empty(&que)){
		tree = queue_pop(&que);
		foreach(tree->data);
		if(tree->left!=NULL)
			queue_push(&que,tree->left);
		if(tree->right!=NULL)
			queue_push(&que,tree->right);
	}
	queue_destroy(&que);
}

bool btree_is_sort(BTree tree){
	if(tree == NULL)
		return true;
	if(tree->left != NULL && tree->left->data >= tree->data){
		return false;
	}
	if(tree->right != NULL && tree->right->data <= tree->data){
		return false;	
	}
	
	return btree_is_sort(tree->left) && btree_is_sort(tree->right);
}

//数组中的元素是否可能是有序二叉树后序遍历的结果
bool arr_is_last_btree(T arr[],size_t n){
	if(n<=1){
        return true;
    }   
    if(n==2){
        return arr[0] != arr[1];
    }   
    int i = 1;
    int mid = 0;
    for(;i<n && arr[i]<arr[0];i++);
    if(i>=n){
        return arr_is_prev_btree(arr+1,n-1);
    }   
    mid = i;
    for(;i<n;i++){
        if(arr[i]<=arr[0]){
            return false;
        }   
    }   
    return arr_is_prev_btree(arr+1,mid-1) && arr_is_prev_btree(arr+mid,n-mid);
}

//数组中的元素是否可能是有序二叉树前序遍历的结果
bool arr_is_prev_btree(T arr[],size_t n){
	if(n<=1)
		return true;
	//arr[0] 根
	if(n==2){
		return arr[0]!=arr[1];	
	}
	int i=1;
	int mid = 0;
	for(i=1;i<n&&arr[i]<arr[0];i++){
		
	}
	if(i>=n){
		return arr_is_prev_btree(arr+1,n-1);	
	}
	mid = i;
	for(;i<n;i++){
		if(arr[i]<=arr[0]){
			return false;	
		}	
	}
	//[1,mid-1] [mid,n-1]  mid-1  n-1-mid+1
	return arr_is_prev_btree(arr+1,mid-1) && arr_is_prev_btree(arr+mid,n-mid);
}

main.c

#include "bintree.h"

void print(T data){
	printf("%d ",data);	
}

int compare(T d1,T d2){
	return d1-d2;	
}
int main(){
	BTree tree = NULL;
	while(1){
		printf("1.插入元素\n");
		printf("2.删除元素\n");
		printf("0.销毁树\n");
		printf("opt:");
		int opt = 0;
		scanf("%d",&opt);
		if(opt == 1){
			int data = 0;
			printf("请输入要插入的元素:");
			scanf("%d",&data);
			int ret = btree_insert(&tree,data,compare);
			if(ret == 0){
				printf("insert success!\n");
			}else{
				printf("insert failed!\n");	
			}
		}else if(opt==2){
			int data = 0;
			printf("请输入要删除的元素:");
			scanf("%d",&data);
			int ret = btree_delete(&tree,data,compare);
			if(ret == 0){
				printf("delete success!\n");	
			}else{
				printf("delete failed!\n");	
			}
		}else if(opt==0){
			btree_clear(&tree);	
			if(btree_is_empty(tree)){
				printf("树已清空!\n");
				break;
			}
		}
		printf("树节点数为:%u\n",btree_size(tree));
		printf("树的高度为:%u\n",btree_height(tree));
		printf("先序遍历:");
		btree_foreach_prev(tree,print);
		printf("\n");
		btree_foreach_prev2(tree,print);
		printf("\n中序遍历:");
		btree_foreach_mid(tree,print);
		printf("\n");
		btree_foreach_mid2(tree,print);
		printf("\n后序遍历:");
		btree_foreach_last(tree,print);
		printf("\n");
		btree_foreach_last2(tree,print);
		printf("\n层序遍历:");
		btree_foreach_layer(tree,print);
		printf("\n");
	}
	return 0;	
}