算法-搜索-接雨水2

算法-搜索-接雨水2

1 题目概述

1.1 题目出处

https://leetcode-cn.com/problems/trapping-rain-water-ii

1.2 题目描述

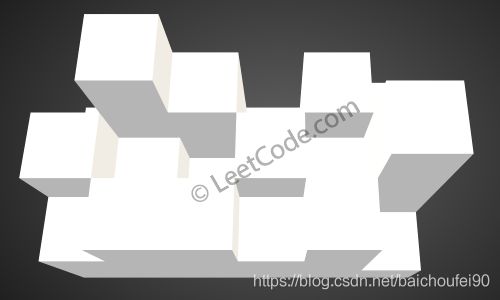
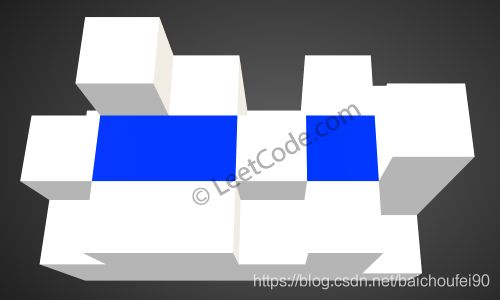
给你一个 m x n 的矩阵，其中的值均为非负整数，代表二维高度图每个单元的高度，请计算图中形状最多能接多少体积的雨水。

示例：

给出如下 3x6 的高度图:
[
[1,4,3,1,3,2],
[3,2,1,3,2,4],
[2,3,3,2,3,1]
]

返回 4 。

如上图所示，这是下雨前的高度图[[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]] 的状态。

下雨后，雨水将会被存储在这些方块中。总的接雨水量是4。

提示：
1 <= m, n <= 110
0 <= heightMap[i][j] <= 20000

2 优先级队列（小顶堆）

2.1 思路

利用木桶效应，蓄水高度取决于最短的那个木板。

我们先将最外围的柱子都放入优先级队列。

然后开始每次从队列内拿出高度最低的，并和四周比较高度，如果高度比当前还低，说明能接水，接完水后还需要放入队列待遍历。

直到队列为空，代表已经遍历完成，返回结果即可。

2.2 代码

class Solution {
    public int trapRainWater(int[][] heightMap) {
        int result = 0;
        int m = heightMap.length;
        if(m < 3){
            return result;
        }
        int n = heightMap[0].length;
        // 用来存储x,y坐标以及高度。高度越低的先出队
        PriorityQueue<int[]> queue = new PriorityQueue<>((o1,o2)->{return o1[2] - o2[2];});
        // 访问数组
        boolean[][] visited = new boolean[m][n];
        // 先将最外围一圈放入优先级对了
        for(int i = 1; i < m-1; i++){
            queue.add(new int[]{i, 0, heightMap[i][0]});
            visited[i][0] = true;
        }
        for(int i = 1; i < m-1; i++){
            queue.add(new int[]{i, n-1, heightMap[i][n-1]});
            visited[i][n-1] = true;
        }
        for(int i = 1; i < n-1; i++){
            queue.add(new int[]{0, i, heightMap[0][i]});
            visited[0][i] = true;
        }
        for(int i = 1; i < n-1; i++){
            queue.add(new int[]{m-1, i, heightMap[m-1][i]});
            visited[m-1][i] = true;
        }
        // 用来往四周查找
        int[] four = {-1, 0, 1, 0, -1};
        // 利用木桶效应，蓄水高度取决于最短的那个木板
        // 开始每次从队列内拿出高度最低的，并和四周比较高度
        // 如果高度比当前还低，说明能接水，接完水后还需要放入队列待遍历
        while(!queue.isEmpty()){
            int[] element = queue.poll();
            for(int i = 0; i < 4; i++){
                int x = element[0] + four[i];
                int y = element[1] + four[i + 1];
                if(x > 0 && x < m - 1 && y > 0 && y < n - 1 && !visited[x][y]){
                    if(heightMap[x][y] < element[2]){
                        result += (element[2] - heightMap[x][y]);

                    }
                    // 取当前遍历节点的高度和四周节点高度的大者为该节点的新高度放入队列
                    // 因为如果四周节点高度小于当前节点，则会蓄水至当前节点高度
                    queue.add(new int[]{x, y, Math.max(heightMap[x][y], element[2])});
                    visited[x][y] = true;
                }
            }
        }
        return result;
    }
}

2.3 时间复杂度

O(N)

• 每个柱子遍历1次

2.4 空间复杂度

O(N)

参考文档

• 优先队列的思路解决接雨水II